Метод Гаусса с выбором максимального элемента по столбцу

Общая схема метода Гаусса для систем, имеющих единственное решение

Пусть 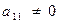. (В противном случае в качестве первого уравнения возьмем какое-либо другое). Разделим первое уравнение на .

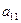Получим

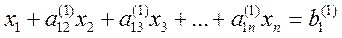, (4)

где ; ,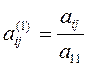

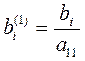
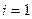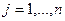
Умножим разрешающее уравнение (4) на 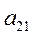и вычтем полученное уравнение из второго уравнения системы (3). Аналогично преобразуем остальные уравнения. Система примет вид

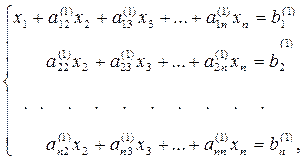(5)

где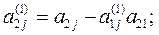

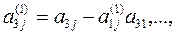
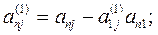
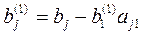
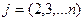
Если какой-либо из коэффициентов 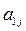окажется равным нулю, то j-ое уравнение системы (3) войдет в систему (5) без изменений т.е.

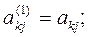
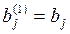
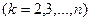
(То есть если в какой-либо из уравнений отсутствовала переменная 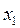, то уравнение не преобразуется). Теперь, оставив без изменения первое уравнение системы (5), сделаем разрешающим второе уравнение и применим описанную процедуру к системе из n-1 уравнений, исключая 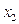из оставшихся уравнений. Получим систему

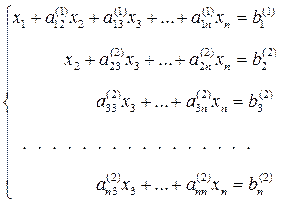
где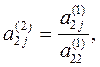

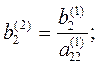
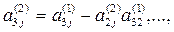
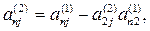
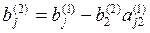
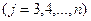
Продолжая аналогичные вычисления, приведем систему (3) к эквивалентной системе с треугольной матрицей коэффициентов

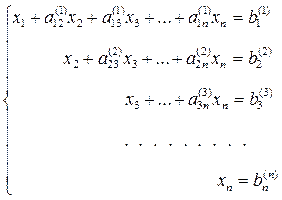(6)

Прямой ход решения выполнен.

Обратный ход:

a) последовательно исключаем неизвестное 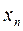, начиная с 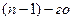уравнения и заканчивая первым. Получаем

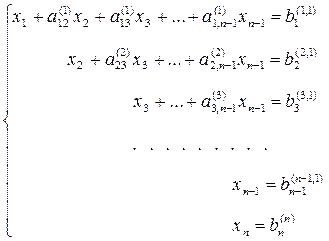(7)

Затем исключаем неизвестное 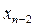из уравнений с номером j

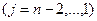и т.д.

В результате получаем решение системы

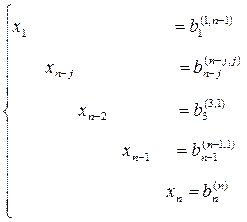
Для уменьшения погрешности вычислений существуют различные модификации метода Гаусса.

В начале первого шага прямого хода среди коэффициентов 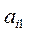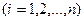при неизвестном 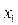находят наибольший по модулю. Пусть это 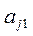. После этого в исходной системе делают перестановку: меняют местами 1-ое и j-ое уравнения. Далее выполняют описанные действия.

В начале второго шага прямого хода максимальный по модулю элемент выбранный среди коэффициентов 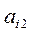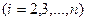при неизвестном 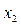. Снова возможна перестановка уравнений и исключение 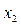из третьего и последующих уравнений и т.д.

При выполнении процедуры прямого хода возможны следующие случаи:

1. матрица А приводится к треугольной (получаю решение).

2. число преобразованных уравнений системы меньше числа неизвестных (ранг матрицы А< n) – Это происходит, если в системе получаются в процессе преобразований тождества 0=0. Система имеет бесконечное множество решений.

3. все коэффициенты при неизвестных в каком-либо уравнении равны нулю, свободный член отличен от нуля. Система не имеет решения.

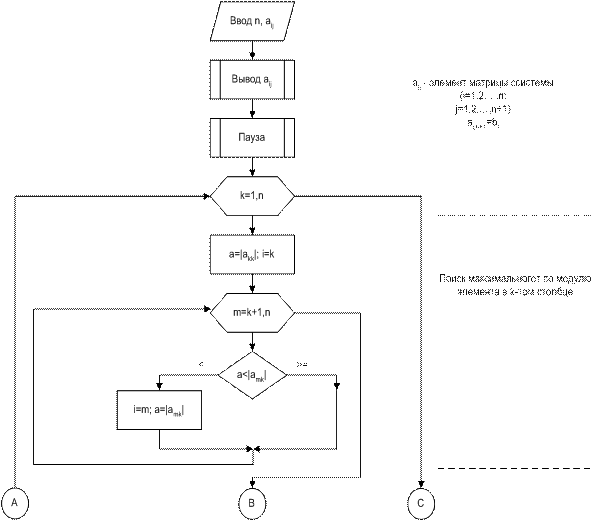
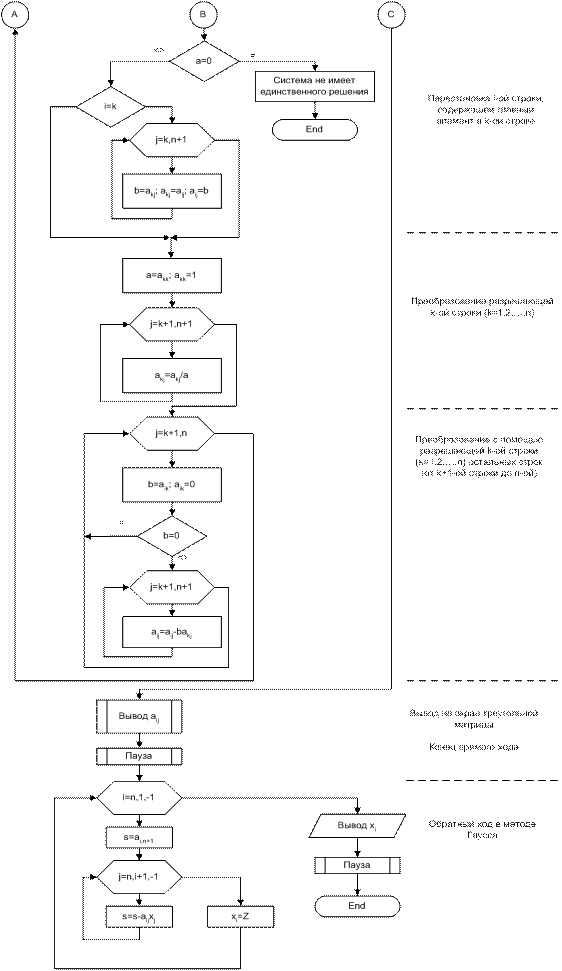
Блок-схема решения системы линейных алгебраических уравнений методом Гаусса с выбором главного элемента (по столбцу)

Дата добавления: 2013-12-12