Определители

Матрицы. Операции над матрицами

Прямоугольной матрицей размера называется совокупность 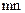чисел, расположенных в виде прямоугольной таблицы, содержащей m строк и n столбцов. Мы будем записывать матрицу в виде

(4.1)

или сокращенно в виде 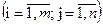. Числа , составляющие данную матрицу, называются ее элементами; первый индекс указывает на номер строки, второй - на номер столбца. Две матрицы и одинакового размера называются равными, если попарно равны их элементы, стоящие на одинаковых местах, то есть , если.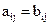

Матрица, состоящая из одной строки или одного столбца, называется соответственно вектор-строкой или вектор-столбцом. Вектор-столбцы и вектор-строки называют просто векторами.

Матрица, состоящая из одного числа, отождествляется с этим числом. Матрица размера , все элементы которой равны нулю, называются нулевой матрицей и обозначается через 0. Элементы матрицы с одинаковыми индексами называют элементами главной диагонали. Если число строк матрицы равно числу столбцов, то есть , то матрицу называют квадратной порядка . Квадратные матрицы, у которых отличны от нуля лишь элементы главной диагонали, называются диагональными матрицами и записываются так:

.

Если все элементы диагональной матрицы равны 1, то матрица называется единичной и обозначается буквой :

.

Квадратная матрица называется треугольной, если все элементы, стоящие выше (или ниже) главной диагонали, равны нулю. Транспонированием называется такое преобразование матрицы, при котором строки и столбцы меняются местами с сохранением их номеров. Обозначается транспонирование значком наверху.

Пусть дана матрица (4.1). Переставим строки со столбцами. Получим матрицу

_,

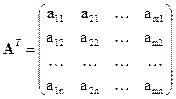которая будет транспонированной по отношению к матрице 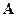. В частности, при транспонировании вектора-столбца получается вектор-строка и наоборот.

Произведением матрицы 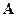на число l называется матрица, элементы которой получаются из соответствующих элементов матрицы 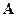умножением на число l: .

Суммой двух матриц и одного размера называется матрица того же размера, элементы которой определяются по формуле.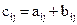

Произведение матрицы 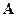на матрицу определяется в предположении, что число столбцов матрицы 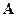равно числу строк матрицы .

Произведением двух матриц и , где , заданных в определенном порядке , называется матрица , элементы которой определяются по следующему правилу:

. (4.2)

Иначе говоря, элементы матрицы-произведения определяются следующим образом: элемент i-й строки и k-го столбца матрицы 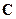равен сумме произведений элементов i-й строки матрицы 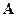на соответствующие элементы k-го столбца матрицы .

Пример 2.1. Найти произведение матрици .

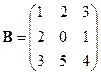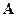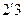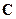Решение. Имеем: матрица размера , матрица размера , тогда произведение существует и элементы матрицы равны

, , ,

, , .

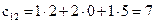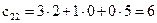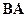, а произведение не существует.

Пример 2.2. В таблице указано количество единиц продукции, отгружаемой ежедневно на молокозаводах 1 и 2 в магазины , и , причем доставка единицы продукции с каждого молокозавода в магазин стоит 50 ден. ед., в магазин ‑ 70, а в ‑ 130 ден. ед. Подсчитать ежедневные транспортные расходы каждого завода.

Молокозавод	Магазин

Решение. Обозначим через 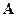матрицу, данную нам в условии, а через ‑ матрицу, характеризующую стоимость доставки единицы продукции в магазины, т.е.,

,.

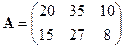Тогда матрица затрат на перевозки будет иметь вид:

.

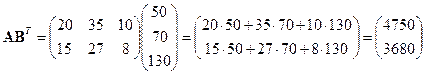Итак, первый завод ежедневно тратит на перевозки 4750 ден. ед., второй ‑ 3680 ден.ед.

Пример 2.3. Швейное предприятие производит зимние пальто, демисезонные пальто и плащи. Плановый выпуск за декаду характеризуется вектором 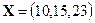. Используются ткани четырех типов ,,,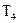. В таблице приведены нормы расхода ткани (в метрах) на каждое изделие. Вектор задает стоимость метра ткани каждого типа, а вектор ‑ стоимость перевозки метра ткани каждого вида.

Изделие	Расход ткани
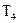
Зимнее пальто
Демисезонное пальто
Плащ

1. Сколько метров ткани каждого типа потребуется для выполнения плана?

2. Найти стоимость ткани, расходуемой на пошив изделия каждого вида.

3. Определить стоимость всей ткани, необходимой для выполнения плана.

4. Подсчитать стоимость всей ткани с учетом ее транспортировки.

Решение. Обозначим через 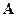матрицу, данную нам в условии, т. е.,

,

тогда для нахождения количества метров ткани, необходимой для выполнения плана, нужно вектор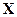умножить на матрицу :

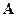Стоимость ткани, расходуемой на пошив изделия каждого вида, найдем, перемножив матрицу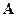и вектор :

.

Стоимость всей ткани, необходимой для выполнения плана, определится по формуле:

Наконец, с учетом транспортных расходов вся сумма будет равна стоимости ткани, т. е. 9472 ден. ед., плюс величина

.

Итак,X (ден. ед).

Перестановкой чисел 1, 2,..., n называется любое расположение этих чисел в определенном порядке. В элементарной алгебре доказывается, что число всех перестановок, которые можно образовать из n чисел, равно 12...n = n!. Например, из трех чисел 1, 2, 3 можно образовать 3!=6 перестановок: 123, 132, 312, 321, 231, 213. Говорят, что в данной перестановке числа i и j составляют инверсию (беспорядок), если i>j, но i стоит в этой перестановке раньше j, то есть если большее число стоит левее меньшего.

Перестановка называется четной (или нечетной), если в ней соответственно четно (нечетно) общее число инверсий. Операция, посредством которой от одной перестановки переходят к другой, составленной из тех же n чисел, называется подстановкой n-ой степени.

Подстановка, переводящая одну перестановку в другую, записывается двумя строками в общих скобках, причем числа, занимающие одинаковые места в рассматриваемых перестановках, называются соответствующими и пишутся одно под другим. Например, символ обозначает подстановку, в которой 3 переходит в 4, 1 ® 2, 2 ® 1, 4 ® 3. Подстановка называется четной (или нечетной), если общее число инверсий в обеих строках подстановки четно (нечетно). Всякая подстановка n-ой степени может быть записана в виде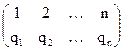, т.е. с натуральным расположением чисел в верхней строке.

Пусть нам дана квадратная матрица порядка n

. (4.3)

Рассмотрим все возможные произведения по n элементов этой матрицы, взятых по одному и только по одному из каждой строки и каждого столбца, т.е. произведений вида:

, (4.4)

где индексы q₁, q₂,..., q_n составляют некоторую перестановку из чисел 1, 2,..., n. Число таких произведений равно числу различных перестановок из n символов, т.е. равно n!. Знак произведения (4.4) равен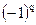^, где q ‑ число инверсий в перестановке вторых индексов элементов.

Определителем n-го порядка, соответствующим матрице (4.3), называется алгебраическая сумма n! членов вида (4.4). Для записи определителя употребляется символ

или

(детерминант, или определитель, матрицы ).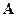

Свойства определителей

1. Определитель не меняется при транспонировании.

2. Если одна из строк определителя состоит из нулей, то определитель равен нулю.

3. Если в определителе переставить две строки, определитель поменяет знак.

4. Определитель, содержащий две одинаковые строки, равен нулю.

5. Если все элементы некоторой строки определителя умножить на некоторое число k, то сам определитель умножится на k.

6. Определитель, содержащий две пропорциональные строки, равен нулю.

7. Если все элементы i-й строки определителя представлены в виде суммы двух слагаемых 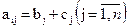, то определитель равен сумме определителей, у которых все строки, кроме i-ой, - такие же, как в заданном определителе, а i-я строка в одном из слагаемых состоит из элементов b_j, в другом - из элементов c_j.

8. Определитель не меняется, если к элементам одной из его строк прибавляются соответствующие элементы другой строки, умноженные на одно и то же число.

Замечание. Все свойства остаются справедливыми, если вместо строк взять столбцы.

Минором элемента a_ij определителя d n-го порядка называется определитель порядка n-1, который получается из d вычеркиванием строки и столбца, содержащих данный элемент.

Алгебраическим дополнением элемента a_ij определителя d называется его минор , взятый со знаком . Алгебраическое дополнение элемента a_ij будем обозначать . Таким образом, .

Способы практического вычисления определителей, основанные на том, что определитель порядка n может быть выражен через определители более низких порядков, дает следующая теорема.

Теорема (разложение определителя по строке или столбцу).

Определитель равен сумме произведений всех элементов произвольной его строки (или столбца) на их алгебраические дополнения. Иначе говоря, имеет место разложение d по элементам i-й строки

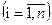
или j- го столбца

В частности, если все элементы строки (или столбца), кроме одного, равны нулю, то определитель равен этому элементу, умноженному на его алгебраическое дополнение.

Пример 2.4. Не вычисляя определителя, показать, что он равен нулю.

Решение. Вычтем из второй строки первую, получим определитель 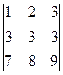, равный исходному. Если из третьей строки также вычесть первую, то получится определитель , в котором две строки пропорциональны. Такой определитель равен нулю.

Пример 2.5. Вычислить определитель 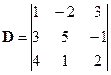, разложив его по элементам второго столбца.

Решение. Разложим определитель по элементам второго столбца:

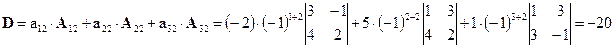Пример 2.6. Вычислить определитель

,

в котором все элементы по одну сторону от главной диагонали равны нулю.

Решение. Разложим определитель 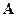по первой строке:

.

Определитель, стоящий справа, можно снова разложить по первой строке, тогда получим:

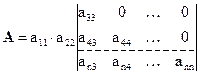
И так далее. После n шагов придем к равенству.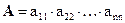

Пример 2.7. Вычислить определитель

.

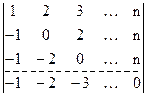Решение. Если к каждой строке определителя, начиная со второй, прибавить первую строку, то получится определитель, в котором все элементы, находящиеся ниже главной диагонали, будут равны нулю. А именно, получим определитель:

,

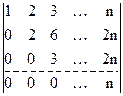равный исходному.

Рассуждая, как в предыдущем примере найдем, что он равен произведению элементов главной диагонали, т.е. n!. Способ, с помощью которого вычислен данный определитель, называется способом приведения к треугольному виду.

Дата добавления: 2013-12-12