Резонанс напряжений

Топографическая и векторная диаграммы

Каждая точка электрической схемы, в которой соединяются элементы схемы, имеет своё значение комплексного потенциала.

Совокупность точек комплексной плоскости, изображающих комплексные потенциалы одноимённых точек электрической схемы, называют топографической диаграммой.

Напряжение между любыми двумя точками электрической схемы, например между точками а и в, по значению и направлению определяются вектором, проведённым на векторной диаграмме от точки в к точке а.

Потенциал любой точки схемы может быть принят равным нулю. На диаграмме эту точку помещают в начало координат. Тогда положение остальных точек схемы на диаграмме определяется параметрами цепи, Э.Д.С. и токами ветвей.

Ток и напряжение на различных участках электрической цепи синусоидального тока, как правило, по фазе не совпадают. Наглядное представление о фазовом расположении различных векторов даёт векторная диаграмма токов и напряжений.

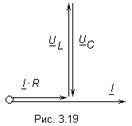
Основной функцией векторной диаграммы является качественный контроль аналитических расчетов, который заключается в сравнении этих векторов, исходя из физических соображений. Например, на векторной диаграмме напряжение 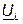должно опережать ток 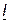на 90⁰, а напряжение 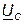отставать от тока 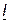на 90⁰.

При несовпадении расчетов с этим положением можно сделать вывод, что в расчете допущена ошибка.

Условием возникновения резонанса напряжений в последовательном RLC - контуре является равенство реактивных сопротивлений катушки и конденсатора.

При 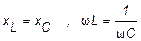значения противоположных по фазе напряжений на индуктивности и на емкости равны, поэтому резонанс в рассматриваемой цепи называют резонансом напряжений.

ü

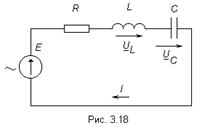Полное сопротивление последовательного контура при резонансе минимально и равно активному сопротивлению.

.

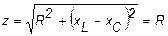ü Из формулы закона Ома 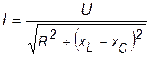следует, что при 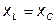ток в контуре максимален и, ввиду чисто активного сопротивления цепи, совпадает по фазе с приложенным напряжением: .

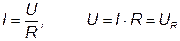ü Напряжение на индуктивности и на емкости равны и в Q раз превышают приложенное напряжение:

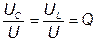. (3.49)

Величина Q называется добротностью контура и показывает во сколько раз напряжение на реактивном (индуктивном или емкостном) элементе превышает напряжение на входе схемы в резонансном режиме. В радиотехнических устройствах Q может достигать 300 и более.

Для добротности контура можно записать также следующие соотношения:

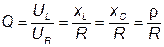, (3.50)

где ρ – волновое (характеристическое) сопротивление контура:

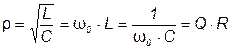. (3.51)

Угловая частота, при которой наступает резонанс, называется резонансной угловой частотой:

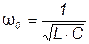. (3.52)

А частота, при которой возникает резонанс – соответственно резонансной частотой.

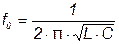. (3.53)

Рассмотрим частотные характеристики последовательного контура, то есть характер изменения ёмкостного и индуктивного сопротивлений при изменении частоты питающего напряжения.

Графики этой зависимости приведены на рис. 3.20.

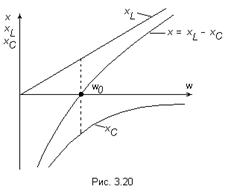Емкостное сопротивление 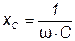при увеличении частоты уменьшается от бесконечности до нуля по закону обратной пропорциональности.

Индуктивное сопротивление 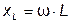при увеличении частоты увеличивается от нуля до бесконечности прямо пропорционально ω.

Как видно из рисунка при увеличении частоты от 0 до 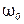реактивное сопротивление 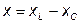имеет емкостной характер и изменяется от 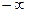до 0. Вследствие этого ток в цепи возрастает от 0 до 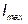, а угол сдвига фаз между напряжением и током изменяется от 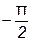до 0. Дальнейшее увеличение частоты от 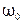до 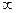приводит к увеличению реактивного сопротивления X от 0 до 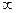, которое будет иметь индуктивный характер.

В результате ток уменьшается от 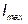до 0, а угол φ возрастает от 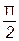до 0. При этом напряжение 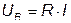изменяется пропорционально току.

Важно отметить, что максимум напряжения на конденсаторе имеет место при частоте немного ниже резонансной, а на индуктивности - при частоте немного выше резонансной. Это можно наблюдать по следующим формулам.

; (3.54)

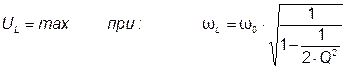; (3.55)

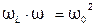. (3.56)

Колебательный контур обладает ещё одним замечательным свойством – избирательностью.

Свойство контура выделять и усиливать сигналы определённой частоты и частот, близких к ней, называется избирательностью.

Для оценки избирательных свойств цепи вводят условное понятие ширины резонансной кривой или полосой пропускания контура, которую определяют как разность верхней и нижней частот, в пределах которых величина мощности в резисторе R составляет не менее 50% от мощности при резонансе:

.

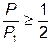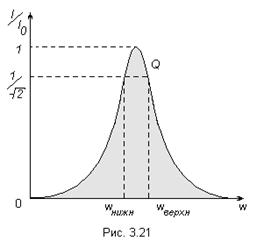
На рис. 3.21 приведена резонансная кривая контура. Из рисунка видно, что чем выше добротность, тем ýже полоса пропускания контура.

Дата добавления: 2013-12-11