ЛЕКЦИЯ №2

Контрольные вопросы

Операции над множествами

Если имеются некоторые множества, то из них можно получить новые с помощью определенных операций.

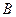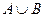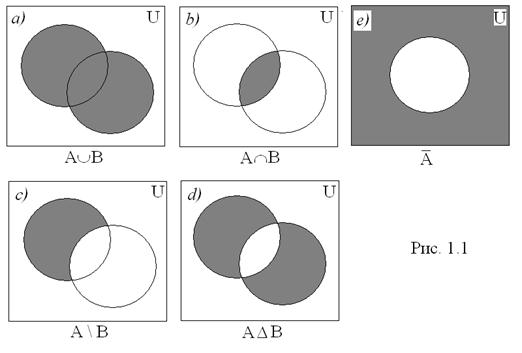
Определение 1.5. Объединением двух множеств и называется множество, которое обозначается и состоит из элементов, принадлежащих хотя бы одному из множеств или 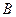. Наглядно это можно продемонстрировать с помощью диаграммы Эйлера-Венна (см. рис. 1.1 а).

Пример 1.4. Рассмотрим два множества 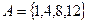и 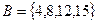. Их объединением 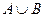будет множество .

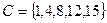Определение 1.6. Пересечением двух множеств и 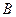называется множество, которое обозначается 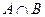и состоит из элементов, принадлежащих каждому из множеств и 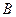(рис.1.1 b).

Пример 1.5. Рассмотрим два множества 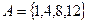и 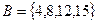. Пересечением этих множеств 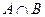будет множество .

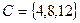Определение 1.7. Разностью двух множеств и 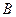называется множество, которое обозначается 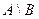и состоит из всех элементов и не принадлежащих множеству 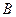(рис.1.1 с).

Пример 1.6. Рассмотрим два множества 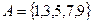и 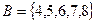. Разностью этих множеств 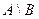будет множество .

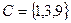Определение 1.8. Симметричной разностью множеств и 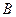называется множество

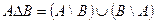(1.4)

т.е. оно состоит из элементов, которые принадлежат либо множеству , либо множеству 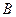(рис.1.1 d).

Пример 1.7. Рассмотрим два множества 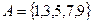и 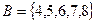. Симметричной разностью этих множеств 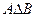будет множество .

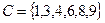Определение 1.9. Дополнением к множеству относительно универсального множества 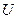называется множество

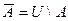(1.5)

На рис.1.1 e приведена диаграмма Эйлера-Венна, поясняющая операцию дополнение.

Пример 1.8. Рассмотрим множество 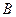={: 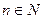, – кратное двум }. В данном случае универсальное множество – множество всех натуральных чисел, т.е. 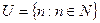. Тогда дополнение множества будет множество .

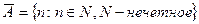1. Сформулируйте понятие множества. 2. Какое множество называется пустым? 3. Подмножество. Какое минимальное число подмножеств имеет любое непустое множество? 4. Конечные и бесконечные множества. Приведите примеры. 5. Основные способы задания множеств? 6. Какое множество называется универсальным? 7. Сформулируйте определение операции объединение. 8. Сформулируйте определение операции пересечение. 9. Сформулируйте определение операции разность. 10. Сформулируйте определение операции симметричная разность. 11. Сформулируйте определение операции дополнение.

Дата добавления: 2013-12-12