
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Практическое применение
|
|
|
|
ВВедение
Глава 1.
Механика как наука, в современном понимании, возникла раньше других разделов физики.
Вся современная физика развилась, в основном, на базе механики, начиная с 17 века. Принципы механики впервые были сформулированы Исааком Ньютоном (1643-1727) в его основном сочинении "Математические начала натуральной философии", первое издание которого вышло в 1687 году. Многие выдающиеся ученые, предшественники Ньютона,- Архимед (ок. 287-212 до н.э.), Иоганн Кеплер (1571-1630), Галилео Галилей (1564-1642), Христиан Гюйгенс (1629-1695) и др., решили немало частных вопросов статики и отчасти динамики. Однако именно Ньютон был первым, кто сформулировал полную систему принципов механики и на их основе создал стройное здание этой науки.
Громадные достижения механики Ньютона, а также его непререкаемый научный авторитет почти на 200 лет отвлекли внимание ученых от недостатков его системы механики. Серьезное критическое отношение к механике Ньютона возникло лишь во второй половине XIX века.
После Ньютона последовало быстрое развитие механики, но до начала XX века оно шло в основном в направлении совершенствования математических методов механики и применения ее законов к все новым и новым областям знания.
Совершенствование механики не затрагивало содержание основных представлений механики Ньютона. Ничего принципиально нового в физические основы механики внесено не было вплоть до XX века, когда положение существенно изменилось.
Положение в корне изменилось с открытием электрических и магнитных явлений, особенно с открытием электромагнитных волн. И их, конечно, пытались объяснить механистически, как волны в некоторой пронизывающей все пространство среде, называемой эфиром (как волны на поверхности воды или звук в воздухе). Однако эти попытки не увенчались успехом.
Второе ограничение классической механики заключается в ее неприменимости к описанию явлений микромира, то есть к движениям тел малой массы в малых участках пространства. Более общей наукой, описывающей такие движения, является квантовая механика.
Третьим ограничение применимости классической механики следует отнести невозможность ее применения в системе с большим количеством частиц.
Объектами изучения классической механики являются медленные движения со скоростью 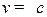 макроскопических тел.
макроскопических тел.
1.2 Механическое движение. Принципы относительности движения.
Определение: Механическим движением называется изменение положения тела по отношению к другим телам.
Если размеры тела при описании его движения несущественны, то его движение можно рассматривать как движение частицы в пространстве.
Это самая простая модель для описания реального тела. Так как в дальнейшем будут рассматриваться движения тела обладающего массой, но в пренебрежении ее размерами, внутренней структуры и формы, то введем в рассмотрение единый термин частица, понимая под ним материальную точку.
Как видно из определения, механическое движение относительно. Для описания движения нам необходима:
система отсчета, которая включает в себя тело отсчета, жестко связанную с ним систему координат и набор синхронизированных между собой часов.
(Слайд из лекции о СО)
1.3 Кинематика материальной точки
Кинематика - это раздел механики, где изучаются способы описания движений независимо от причин, обусловливающих эти движения, то есть, в основном, геометрические свойства движения.
1.3.1 Способы описания движения
Существует три способа описания движения частицы: векторный (геометрический), координатный и естественный. Рассмотрим их последовательно, учитывая, то аналогичное построение описания движения частицы будет применимо в релятивистском случае.
Естественный способ указывается траектория точки, закон ее движения по этой траектории, начало и направление отсчета дуговой координаты: s=f(t) – закон движения точки. При прямолинейном движении: х=f(t).
Этот способ применяется, когда заранее известна траектория Например рельсы определяют траекторию трамвая, поэтому для него хорош естественный способ.
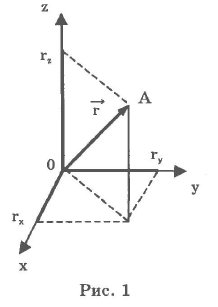
Векторный способ требует введения понятия "радиус-вектор".
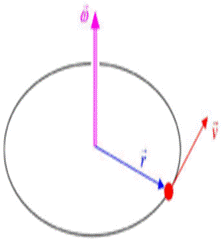
Радиусом-вектором (r) называется направленный отрезок, соединяющий начало координат и точку с произвольными координатами. Положение точки в пространстве в заданной системе отсчета будет полностью определено, если известен r (его положение относительно осей координат и его размеры) (рис. 1).
. 
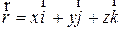 (1)
(1)
В этом способе положение интересующей нас частицы А задают радиусом-вектором 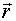 , проведенным из некоторой неподвижной точки О выбранной системы отсчета в точку А.
, проведенным из некоторой неподвижной точки О выбранной системы отсчета в точку А.
При движении частицы А ее радиус-вектор меняется в общем случае как по модулю, так и по направлению, т. е. радиус-вектор 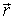 зависит от времени t.
зависит от времени t.
(слайд 10)
Следовательно, для того чтобы определить местоположение точки через какой-то промежуток времени t1, необходимо знать начальный радиус-вектор и радиус –вектор определяющий конечное положение материальной точки за промежуток времени t1.
Эта же задача может быть решена, если известны начальные координаты и их приращение за промежуток времени t1
Геометрическое место точек, где тело побывало за время своего движения, называется траекторией частицы А.
При векторном способе описания траекторией будет положение концов радиус-вектора 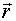 во все моменты времени.
во все моменты времени.
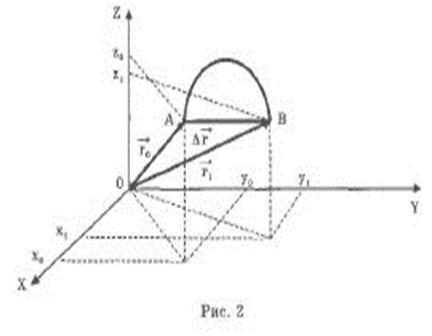
Вектор перемещения  частицы А представляет собой приращение радиус
частицы А представляет собой приращение радиус 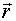 за время t1:
за время t1: 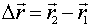 .
.
Отношение 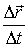 называют средним вектором скорости <
называют средним вектором скорости <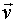 > за время t1.
> за время t1. 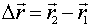 .
.
Слайд (26)
Вектор <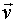 > совпадает по направлению с
> совпадает по направлению с 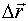 .
.
Определим теперь вектор мгновенной скорости 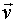 частицы как предел отношения
частицы как предел отношения 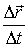
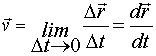 (2)
(2)
Это значит, что вектор мгновенной скорости 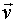 частицы в данный момент времени равен производной от радиус-вектора
частицы в данный момент времени равен производной от радиус-вектора 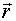 по времени и направлен по касательной к траектории в данной точке в сторону движения частицы А (как и вектор
по времени и направлен по касательной к траектории в данной точке в сторону движения частицы А (как и вектор 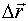 ). Модуль вектора
). Модуль вектора 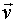 равен
равен
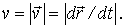 (3)
(3)
Из формул (1) и (2) следует, что вектор скорости в декартовой системе координат может быть записан:
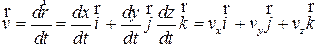 (4)
(4)
Движение частицы характеризуется также ускорением. Вектор ускорения 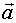 определяет скорость изменения вектора скорости
определяет скорость изменения вектора скорости 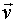 со временем:
со временем:
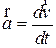 (5)
(5)
т. е. равен производной от вектора скорости по времени. Направление вектора 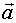 совпадает с направлением вектора
совпадает с направлением вектора 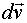 - приращением вектора
- приращением вектора 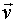 за время dt.
за время dt.
Вектор ускорения в декартовой системе координат может быть записан:
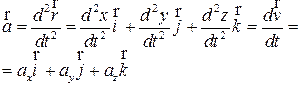 (6).
(6).
Координатный способ – это способ описания движения при котором в любой момент времени для описания движения тела необходимо указывать его координаты т.е.
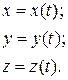
Прикладная часть (примеры решения задач)
Рассмотрим на примере движение материальной точки.
Пусть, например, радиус-вектор частицы зависит от времени t по закону
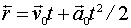 ,
,
где 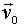 и
и 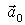 - постоянные векторы. Найдем скорость
- постоянные векторы. Найдем скорость 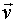 и ускорение
и ускорение 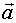 частицы:
частицы: 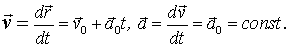
Модуль вектора скорости
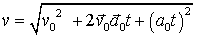 .
.
Таким образом, зная зависимость  , можно найти скорость
, можно найти скорость 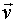 и ускорение
и ускорение 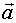 частицы в каждый момент времени.
частицы в каждый момент времени.
Возникает и обратная задача: можно ли найти 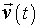 и
и 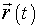 , зная зависимость от времени ускорения
, зная зависимость от времени ускорения 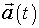 ?
?
Оказывается, для получения однозначного решения этой задачи одной зависимости 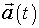 недостаточно, так как необходимо еще знать начальные условия, а именно - скорость
недостаточно, так как необходимо еще знать начальные условия, а именно - скорость 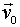 и радиус-вектор
и радиус-вектор 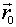 частицы в некоторый начальный момент
частицы в некоторый начальный момент 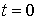 .
.
Чтобы в этом убедиться, рассмотрим простой случай, когда при движении ускорение частицы 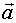 остается постоянным.
остается постоянным.
Определим сначала скорость частицы 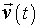 . Согласно (5), за интервал времени dt малое приращение скорости
. Согласно (5), за интервал времени dt малое приращение скорости 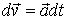 . Интегрируя это выражение по времени от t = 0 до t, определим конечное приращение вектора скорости за это время:
. Интегрируя это выражение по времени от t = 0 до t, определим конечное приращение вектора скорости за это время:
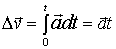 .
.
Но величина 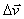 - это еще не искомая скорость
- это еще не искомая скорость 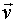 . Для нахождения
. Для нахождения 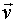 , необходимо знать скорость
, необходимо знать скорость 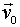 в начальный момент времени
в начальный момент времени 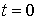 . Тогда
. Тогда 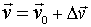 , или
, или
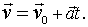
Аналогично вычисляется и радиус-вектор 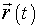 частицы.
частицы.
Рассмотрим произвольное движение материальной точки.
Пусть точка движется по заранее известной траектории (естественный способ описания движения).
 Рис.2
Рис.2
Рассмотрим как в этом способе описания определяется скорость частицы. Введем единичный вектор 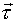 , связанный с движущейся точкой А и направленный по касательной к траектории в сторону увеличения дуговой координаты l (рис. 2.). Ясно, что
, связанный с движущейся точкой А и направленный по касательной к траектории в сторону увеличения дуговой координаты l (рис. 2.). Ясно, что 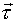 - переменный вектор: его направление зависит от l, хотя длина этого вектора остается неизменной. Вектор скорости
- переменный вектор: его направление зависит от l, хотя длина этого вектора остается неизменной. Вектор скорости 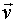 частицы А направлен по касательной к траектории, поэтому его можно согласно (4) выразить так:
частицы А направлен по касательной к траектории, поэтому его можно согласно (4) выразить так:
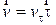 (7)
(7)
где 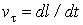 - (8)
- (8)
проекция вектора 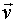 на направление вектора
на направление вектора 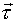 , причем
, причем 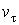 - величина алгебраическая.
- величина алгебраическая.
Кроме того, ясно, что
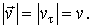
Найдем ускорение частицы 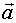 .
.
Согласно (7) и (8) получаем:
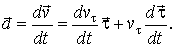 (9)
(9)
Преобразуем последнее слагаемое этого выражения используя прием неявного дифференцирования:
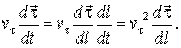 (10) (10)
|
Рассмотрим приращение вектора  на участке d l. Для этого выделим на траектории движения l, элемент d l и нарисуем его более крупно(рис. 3).
на участке d l. Для этого выделим на траектории движения l, элемент d l и нарисуем его более крупно(рис. 3).
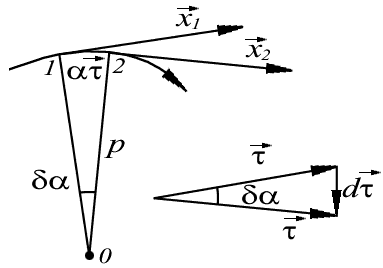
рис.3
Из схемы движения видно, что при стремлении точки 2 к точке 1 отрезок траектории между ними можно представить в виде дуги окружности с центром в некоторой точке О.
Ее называют центром кривизны траектории в данной точке, а радиус 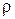 соответствующей окружности - радиусом кривизны траектории в той же точке.
соответствующей окружности - радиусом кривизны траектории в той же точке.
Как видно из рис. 3, угол
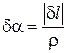 . (11)
. (11)
Если ввести единичный вектор нормали 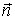 к траектории в точке 1, направленный к центру кривизны, то последнее равенство запишется в векторном виде:
к траектории в точке 1, направленный к центру кривизны, то последнее равенство запишется в векторном виде:
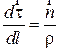 (12)
(12)
Подставляя (12) в (10) получаем для вектора ускорения 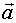
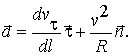
| (13) |
Здесь первое слагаемое называют тангенциальным ускорением 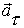 , а второе - нормальным (центростремительным)
, а второе - нормальным (центростремительным) 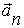 .
.
Модуль полного ускорения в вычисляется по теореме Пифагора (рис.4):
Рис.4 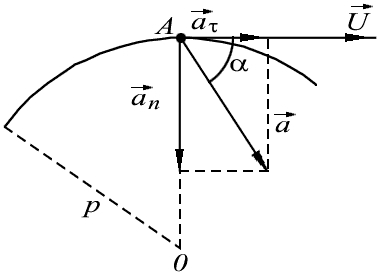
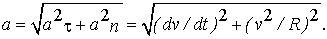 (14)
(14)
Найдем полное ускорение и угол между вектором полного ускорения и вектором скорости частицы как функцию координаты l. Частицы, двигается по криволинейной траектории радиуса 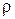 , причем ее скорость зависит от длины пути l по закону:
, причем ее скорость зависит от длины пути l по закону:
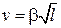 .
.
где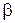 постоянная.
постоянная.
Из рис. 4 видно, что угол 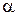 можно определить из соотношения составляющих полного ускорения по формуле
можно определить из соотношения составляющих полного ускорения по формуле 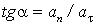 .
.
Значения компонент вектора полного ускорения 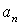 и
и 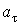 . Вычисляются по формулам:
. Вычисляются по формулам:
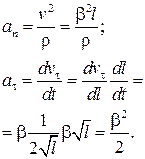
Отсюда получаем 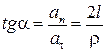 .
.
Задача 2. (дописать)
Лекция 2.
2.1 Кинематика движения твердого тела.
Следующей по сложности модельной задачей после частицы рассмотрим движение твердого тела.
Твердое тело – Это совокупность материальных точек, расстояние между которыми не меняется в процессе движения.
Полученные нами результаты будут неоднократно использоваться в дальнейшем.
В настоящее время рассматривают пять видов движения твердого тела:
1)поступательное, если прямая, соединяющая любые две точки тела, перемещается, оставаясь параллельной своему начальному положению, например движение трамвая на прямом участке пути;
2) вращательное, если все точки лежащие на некоторой прямой, называемой осью вращения, остаются неподвижными, например движение двери при открывании и закрывании;
3) плоское, если все точки тела движутся в плоскостях, параллельных некоторой плоскости, неподвижной в рассматриваемой системе отсчета, например качение колеса на прямом участке пути;
4)свободное, если нет перечисленных выше четырех ограничений, например движение свободного произвольного брошенного тела вблизи поверхности Земли.
Первые два движения являются основными движениями твердого тела. Можно показать, что остальные виды движения твердого тела можно свести к одному из основных движений или к их совокупности.
Приступим к рассмотрению вышеуказанных типов движения
При поступательном движении все точки твердого тела совершают равные перемещения за один и тот же промежуток времени. Поэтому скорости и ускорения всех точек тела в данный момент времени одинаковы. Этот факт позволяет свести изучение поступательного движения твердого тела к изучению движения отдельной частицы тела, т. е. к задаче кинематики частицы.
Таким образом, поступательное движение твердого тела может быть полностью описано, если известны зависимость от времени радиус-вектора 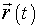 любой точки этого тела и его положение в начальный момент, что уже было рассмотрено нами ранее.
любой точки этого тела и его положение в начальный момент, что уже было рассмотрено нами ранее.
Пример на слайде
Рассмотрим вращательное движение вокруг неподвижной оси 00'.
Пусть твердое тело, вращаясь вокруг нее, совершило за время dt бесконечно малый поворот на угол, который будем характеризовать вектором 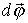 , модуль его равен
, модуль его равен 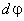 , а направление совпадает с осью 00', причем так, что направление поворота отвечает правилу правого винта по отношению к направлению вектора
, а направление совпадает с осью 00', причем так, что направление поворота отвечает правилу правого винта по отношению к направлению вектора 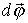 (рис. 5).
(рис. 5).
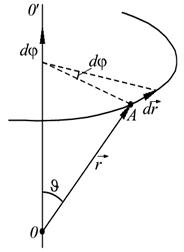 Рис.5
Рис.5
Введем теперь векторы угловой скорости и углового ускорения таким же способом, как мы вводили векторы 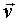 и
и 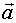 .
.
Вектор угловой скорости 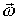 определяют так
определяют так
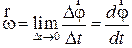 (15)
(15) 
Как следует из (15) направление вектора угловой скорости определяется направлением изменения вектора угла вращения.
Единицей измерения угловой скорости в СИ является радиан в секунду (рад/с).
Изменение вектора 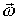 со временем характеризуют вектором углового ускорения
со временем характеризуют вектором углового ускорения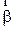 , который определяют соотношением
, который определяют соотношением
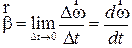 (16)
(16)
Аналогично, из (16) следует, что направление углового ускорения совпадает с направлением приращения вектора угловой скорости.
Единицей измерения углового ускорения в СИ является радиан на секунду в квадрате (рад/с2).
По известной зависимости 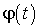 , называющейся законом вращения тела, формулы (15) и (16) дают возможность определить угловую скорость и угловое ускорение в любой момент времени. Из зависимости углового ускорения от времени и начальных условий, т. е. угловой скорости
, называющейся законом вращения тела, формулы (15) и (16) дают возможность определить угловую скорость и угловое ускорение в любой момент времени. Из зависимости углового ускорения от времени и начальных условий, т. е. угловой скорости 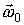 и угла
и угла 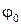 в начальный момент времени, можно найти
в начальный момент времени, можно найти 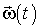 и
и 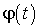 .
.
Рассмотрим следующий пример:
Пусть твердое тело вращается вокруг неподвижной оси по закону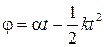 , где
, где 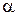 и
и 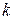 - некоторые положительные постоянные. Определим движения тела.
- некоторые положительные постоянные. Определим движения тела.
Согласно (15) и (16),.
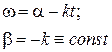
Из полученных соотношений видно, что тело вращается равнозамедленно, останавливается в момент времени 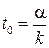 , а затем начинает вращаться в противоположном направлении.
, а затем начинает вращаться в противоположном направлении.
2.3 Связь между линейными и угловыми величинами
Установим связь между линейными и угловыми величинами.
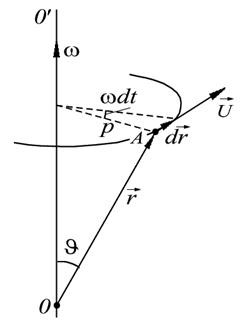 Рис.6
Рис.6
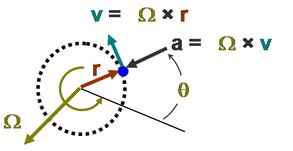
Пусть положение точки А относительно некоторой точки О, лежащей на оси вращения характеризуется радиус-вектором 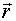 (рис.6).
(рис.6).
Найдем элементарное перемещение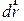 любой частицы А твердого тела при таком повороте
любой частицы А твердого тела при таком повороте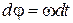 .
.
Как следует из нашего рисунка
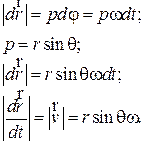
Полученное выражение можно записать через векторное произведение
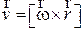 . (17)
. (17)
Векторное произведение:
Вектор скорости должен быть перпендикулярен как вектору угловой скорости так и радиусу вектору.
Направление сектора скорости определяется путем поворота правым винтом от первого вектора в векторном произведении ко второму.
Дифференцирование уравнения (17) по времени по определению скорости дает ускорение 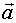 частицы А:
частицы А: 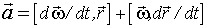 , или
, или
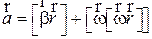 (18)
(18)
Так как в рассматриваемом случае ось вращения неподвижна, то угловая скорость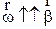 и первое слагаемое –тангенциальное ускорение, а второе нормальное или центростремительное.
и первое слагаемое –тангенциальное ускорение, а второе нормальное или центростремительное.
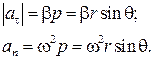
Модуль полного ускорения равен:
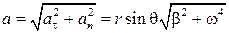 (19).
(19).
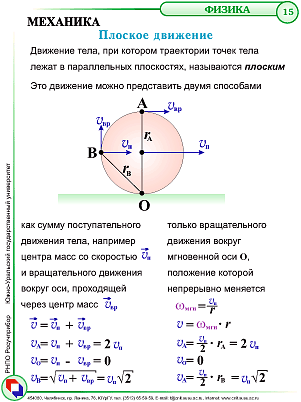
2.4 Плоское движение
Плоское движение - это такое движение, при котором каждая точка твердого тела движется в плоскости, параллельной некоторой неподвижной в данной системе отсчета плоскости.
|
| Рис7 |
За рамки нашего основного курса выносится более подробное рассмотрение плоского движения. Скажу лишь, что из проделанного нами опыта мы видим, что плоское движение твердого тела можно представить как поступательное движение тела (вместе с произвольной точкой О) и вращательного (вокруг оси, проходящей через точку О, которую называют мгновенной осью вращения.
Положение мгновенной оси со временем меняется.
Например, у катящегося по плоскости цилиндра, мгновенная ось, в каждый момент, совпадает с линией касания цилиндра и плоскости.
(какой нибудь рисунок при мгновенную ось вращения)
Глава 2. Динамика
Далее рассматриваются законы Ньютона для частицы (материальной точки), которые служат основой для рассмотрения причин движения произвольных тел.
2.1 Первый закон Ньютона
В кинематике, где только описываются движения и не затрагивается вопрос о причинах, их вызывающих, никакой принципиальной разницы между различными системами отсчета нет, и все они в этом отношении равноправны.
Иначе обстоит дело в динамике, где изучаются законы движения. Здесь обнаруживается существенное различие между разными системами отсчета и преимущества одного класса систем отсчета по сравнению с другим.
Утверждение, что инерциальные системы отсчета существуют, составляет содержание
Первого закона классической механики - закона инерции Галилея - Ньютона –
таково: существуют системы отсчета, называемые инерциальными, в которых при отсутствии воздействия других тел частица сохраняет стационарное состояние движения: движется равномерно и прямолинейно (в частном случае - покоится).
Существование инерциальных систем отсчета подтверждается опытом. Первоначальными опытами было установлено, что такой системой отсчета является Земля. Последующие более точные опыты показали, что эта система отсчета не совсем инерциальная: были обнаружены ускорения, существование которых нельзя объяснить действием каких-либо определенных тел - необходимо учитывать вращение Земли и ее движение вокруг Солнца (опыт Фуко по сохранению неизменной плоскости качания маятника с шаровым подвесом без трения и все аналогичные ему). Заметим, что во многих случаях систему отсчета, связанную с Землей, можно считать практически инерциальной.
В то же время наблюдения над ускорениями планет показали инерциальность гелиоцентрической системы отсчета (система Коперника, в честь Николая Коперника, 1473-1543), связанной с центром Солнца и "неподвижными" звездами. В настоящее время инерциальность гелиоцентрической системы отсчета подтверждается всей совокупностью опытов в пределах точности имеющихся измерений. Любая другая система отсчета, движущаяся равномерно и прямолинейно относительно гелиоцентрической системы, является также инерциальной. Действительно, если в гелиоцентрической системе отсчета ускорение тела равно нулю, то оно равно нулю и в любой другой из этих систем отсчета.
Таким образом, существует не одна, а бесчисленное множество инерциальных систем отсчета, движущихся относительно друг друга прямолинейно и равномерно.
Важной особенностью инерциальных систем отсчета является наличие, определенных свойств симметрии времени и пространства. Опыт убеждает, что в этих системах отсчета время однородно, а пространство однородно и изотропно. Свойства симметрии пространства и времени тесно связаны с законами сохранения и определяют их количество.
Однородность времени заключается в том, что протекание физических явлений (в одних и тех же условиях) в разное время их наблюдения одинаково. Иначе говоря, различные моменты времени эквивалентны друг другу по своим физическим свойствам.
Однородность и изотропность пространства заключаются в том, что свойства пространства одинаковы в различных точках (однородность), а в каждой точке одинаковы во всех направлениях (изотропность).
Для инерциальных систем отсчета справедлив принцип относительности Галилея, согласно которому
все инерциальные системы по своим механическим свойствам эквивалентны друг другу.
Это значит, что никакими механическими опытами, проводимыми "внутри" данной инерциальной системы, нельзя установить, покоится эта система отсчета или движется. Во всех инерциальных системах отсчета свойства пространства и времени одинаковы, одинаковы также и все законы механики.
Это утверждение - один из важнейших принципов классической механики. Оно является обобщением опыта и подтверждается всем многообразием приложений классической механики к движению тел, скорости которых значительно меньше скорости света.
Все сказанное ясно свидетельствует об исключительности свойств инерциальных систем отсчета, в силу которых именно эти системы должны, как правило, использоваться при изучении механических явлений.
2.3 Второй Закон Ньютона
После того, как мы с Вами вспомнили некоторые силы и опытные факты, описывающие действие одних тел на другие можно, необходимо также вспомнить, что каждое тело сопротивляется действию других тел.
Это свойство, выражающее степень сопротивления тела к изменению его скорости, называют инертностью. У различных тел оно проявляется в разной степени. Мерой инертности служит величина, называемая массой. Тело с большей массой является более инертным, и наоборот.
Второй закон Ньютона – это закон, с помощью которого, можно описать поведение материальной точки под действием сил, на нее действующих
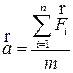 (31)
(31)
Второй закон Ньютона утверждает: в инерциальных системах ускорение приобретаемое материальной точкой (телом) прямо пропорционально векторной сумме вызывающих его сил, совпадает с нею по направлению и обратно пропорционально массе материальной точки (тела).
Иногда этот закон Ньютона записывают в другой форме придавая немного другой смысл.
Говорят: произведение массы материальной точки на ее ускорение является функцией положения этой точки относительно окружающих ее тел, а иногда даже функцией ее скорости. Эту функцию обозначают F и называют силой.
Дополняют такое описание понятием импульс тела, который определяется как произведение массы тела на его скорость
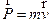
Запишем закон Ньтона
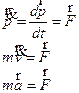
Если F =0, то P= const.
|
|
|
|
Дата добавления: 2013-12-12; Просмотров: 1145; Нарушение авторских прав?; Мы поможем в написании вашей работы!