
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Связь между линейной и угловой скоростью
|
|
|
|
Пусть за малый промежуток времени Dt тело повернулось на угол Dj (рис. 2.17). Точка, находящаяся на расстоянии R от оси, проходит при этом путь DS = R×Dj. По определению линейная скорость точки будет равна
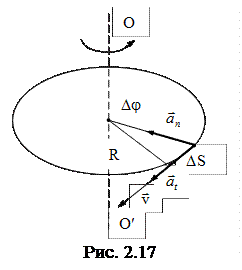
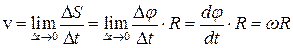 .
.
Итак, v = w·R и чем дальше отстоит точка от оси вращения, тем с большей линейной скоростью она движется.
Найдем теперь линейное ускорение точек вращающегося тела. Нормальное ускорение равно
 . Итак,
. Итак, 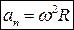
Модуль тангенциального ускорения 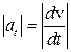 .
.
Отсюда
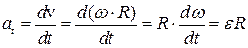 .
.
Итак,
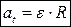 (2.7)
(2.7)
Таким образом, как нормальное, так и тангенциальное ускорения растут линейно с увеличением R (R – расстояние от точки до оси вращения).
Полученное ранее уравнение v=wR устанавливает связь между модулями векторов 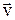 и
и 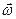 . Пользуясь специальным математическим аппаратом («векторное исчисление») можно установить связь между самими векторами.
. Пользуясь специальным математическим аппаратом («векторное исчисление») можно установить связь между самими векторами.
 Известно: векторным произведением двух векторов
Известно: векторным произведением двух векторов  и
и  называется вектор
называется вектор  (обозначение:
(обозначение: 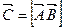 ), обладающий следующими свойствами:
), обладающий следующими свойствами:
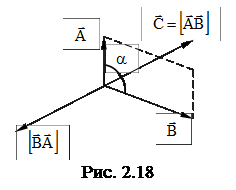
1. Модуль вектора 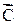 равен произведению модулей перемножаемых векторов на синус угла a между ними (рис. 2.18).
равен произведению модулей перемножаемых векторов на синус угла a между ними (рис. 2.18).
2. Вектор 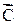 перпендикулярен к плоскости, в которой лежат вектора
перпендикулярен к плоскости, в которой лежат вектора 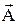 и
и 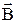 , причем направление его связано с направлениями
, причем направление его связано с направлениями 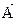 и
и 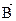 по правилу правого винта: если смотреть вслед вектору
по правилу правого винта: если смотреть вслед вектору 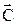 , то совершаемый по кратчайшему пути поворот от первого сомножителя ко второму осуществляется по часовой стрелке.
, то совершаемый по кратчайшему пути поворот от первого сомножителя ко второму осуществляется по часовой стрелке.
Пусть тело вращается вокруг оси Z с угловой скоростью w (рис. 2.19). Легко видеть, что векторное произведение 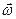 на радиус–вектор
на радиус–вектор 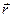 точки, скорость
точки, скорость 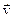 которой мы хотим найти, представляет собой вектор, совпадающий по направлению с вектором
которой мы хотим найти, представляет собой вектор, совпадающий по направлению с вектором 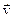 и имеющий модуль, равный w×r× sin a=w×R, т.е. v.
и имеющий модуль, равный w×r× sin a=w×R, т.е. v.
Таким образом, векторное произведение
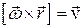 .
.
Иногда применяют другие обозначения векторного произведения
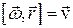 или
или 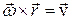
Учитывая, что 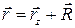 , получим
, получим
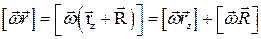
Первое слагаемое в последнем выражении равно нулю, т.к. sina = 0. Следовательно, 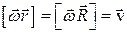 .
.
Итак,
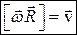 , (2.8)
, (2.8)
где 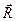 - перпендикулярная к оси вращения составляющая радиус-вектора
- перпендикулярная к оси вращения составляющая радиус-вектора 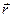 , проведенного из точки, взятой на оси.
, проведенного из точки, взятой на оси.
Модулю векторного произведения можно дать простую геометрическую интерпретацию: выражение AB· sina численно равно площади параллелограмма, построенного на векторах 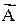 и
и 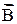 (рис. 2.20), вектор
(рис. 2.20), вектор 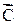 в этом случае ^ плоскости чертежа и направлен за чертеж.
в этом случае ^ плоскости чертежа и направлен за чертеж.
|

| ЛЕКЦИЯ 3 |
|
|
|
|
Дата добавления: 2013-12-12; Просмотров: 2378; Нарушение авторских прав?; Мы поможем в написании вашей работы!
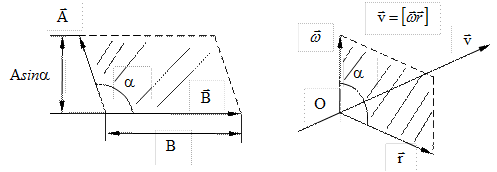 Рис. 2.20
Рис. 2.20