Импульс. Закон сохранения импульса

В механической системе, состоящей из нескольких тел, существуют как силы взаимодействия между телами системы, которые называются внутренними, так и силы взаимодействия этих тел с телами, не входящими в данную систему, которые называются внешними. Если внешние силы отсутствуют, то механическая система называется замкнутой.

Для замкнутой механической системы существует несколько физических величин, которые остаются постоянными с течением времени. Одной из таких величин является импульс тела, который является вектором и равен произведению массы тела m на вектор скорости тела v: p = m v. Для механической системы ее импульс равен векторной сумме импульсов, составляющих ее n тел:

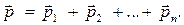
Пользуясь выражением для импульса и учитывая постоянство массы тела, представим второй закон Ньютона в следующем виде:

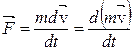(3.2)

Рассмотрим изолированную систему, состоящую из двух движущихся тел. Сталкиваясь друг с другом, тела (упругие шары) будут изменять свой импульс. Рассматривая взаимодействие тел в течение небольшого промежутка времени Dt и применяя к каждому телу закон изменения импульса, можно записать:

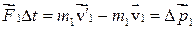
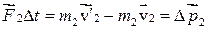
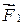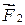, – результирующие силы, действующие на каждое тело,

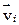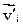, – скорости в начале и в конце рассматриваемого промежутка времени.

Складывая равенства почленно, получим:

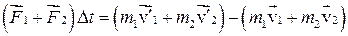
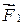и 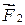– силы внутренние, тогда по III закону Ньютона =-.

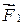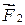Тогда

.

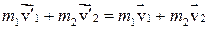Это означает, что сумма импульсов обеих тел системы не изменяется со временем, т.е. .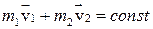

Введем величину 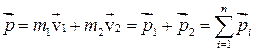, представляющую вектор импульса всей системы (или полный импульс системы).

Тогда для системы из “n” тел

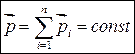(3.3)

или из II закона Ньютона

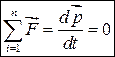, (3.4)

т.к. система замкнута.

Эти равенства выражают закон сохранения импульса.

ОПРЕДЕЛЕНИЕ: Полный вектор импульса замкнутой (или изолированной) системы тел с течением времени не изменяется.

Пусть теперь на тела A и B действуют теперь как внутренние, так и внешние силы: на тело A – 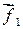и 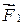, а на тело B – 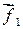и .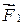

Тогда ,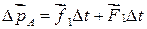

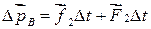
или, что равносильно для системы из “n” тел: .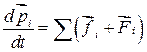

Складывая эти уравнения с учетом, что 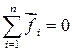, получаем

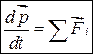. (3.5)

Следовательно, производная по времени от вектора импульса системы равна сумме всех внешних сил, приложенных к телам системы.

Для замкнутой системы 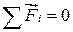, вследствие чего полный импульс не зависит от времени. Это утверждение представляет собой содержание закона сохранения импульса. Повторим его:

ОПРЕДЕЛЕНИЕ: Импульс замкнутой системы тел остается постоянным.

Отметим, что импульс системы тел остается постоянным и для системы, подверженной внешним воздействиям, при условии, что внешние силы, действующие на тела системы, в сумме дают нуль. Если даже сумма внешних сил не равна нулю, но проекция этой суммы на некоторое направление есть нуль, то составляющая импульса в этом направлении будет постоянной.

Дата добавления: 2013-12-12