Работа внешних сил при вращательном движении твердого тела

Найдем работу, которую совершают силы при вращении тела вокруг неподвижной оси Z.

Пусть на массу действуют внутренняя сила 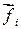и внешняя сила 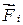(результирующая сила лежит в плоскости, перпендикулярной оси вращения) (рис. 4.19). Эти силы совершают за время dt работу:

.

Осуществив в смешанных произведениях векторов циклическую перестановку сомножителей, находим:

,

где ,– соответственно, моменты внутренней и внешней сил относительно точки «О».

Просуммировав по всем элементарным массам, получим элементарную работу, совершаемую над телом за время dt:

.

Сумма моментов внутренних сил равна нулю. Тогда, обозначив суммарный момент внешних сил через 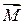, придем к выражению:

.

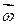Известно, что скалярным произведением двух векторов называется скаляр, равный произведению модуля одного из перемножаемых векторов на проекцию второго на направление первого, учтя, что , (направления оси Z и совпадают), получим

,

но w· dt = d j, т.е. угол, на который поворачивается тело за время dt. Поэтому

.

Знак работы зависит от знака M_z, т.е. от знака проекции вектора 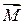на направление вектора .

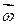Итак, при вращении тела внутренние силы работы не совершают, а работа внешних сил определяется формулой .

Работа за конечный промежуток времени находится путем интегрирования

.

Если проекция результирующего момента внешних сил на направление 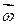остается постоянной, то ее можно вынести за знак интеграла:

, т.е. .

Т.е. работа внешней силы 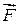при вращательном движении тела равна произведению проекции момента внешней силы на направление 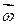и угол поворота.

С другой стороны работа внешней силы, действующей на тело идет на приращение кинетической энергии тела (или равна изменению кинетической энергии вращающегося тела). Покажем это:

и тогда

;

Следовательно,

. (4.7)

Самостоятельно:

Упругие силы;

Закон Гука.

ЛЕКЦИЯ 7

Дата добавления: 2013-12-12