Течение жидкости в круглой трубе

Ламинарное и турбулентное течения.

При достаточно малой скорости движения жидкости наблюдается слоистое или ламинарное течение, когда слои жидкости скользят относительно друг друга не перемешиваясь. При ламинарном течении положение линий тока с течением времени не меняется, такое течение является стационарным. С увеличением скорости движения частиц течение жидкости становится нестационарным, наблюдаются завихрения, скорость течения в каждой точке пространства беспорядочно меняется. Такое течение называется турбулентным.

Английский ученый Рейнольдс установил, что характер течения зависит от значения безразмерной величины:

Re=rvl/h, (5.9)

где r - плотность жидкости; v - средняя скорость потока; l - характерный для поперечного сечения размер, например, радиус при круглом сечении; h - коэффициент вязкости. Величина Re называется числомРейнольдса. При малых значениях числа Re наблюдается ламинарное течение. Начиная с некоторого определенного значения этого числа, называемого критическим, течение приобретает турбулентный характер. Отношение n = h/r называется кинематической вязкостью. Используя n, число Рейнольдса можно записать в следующем виде: Re =vl/n. Характер течения различных жидкостей в трубах различных сечений будет совершенно одинаков, если каждому течению соответствует одно и то же значение Re.

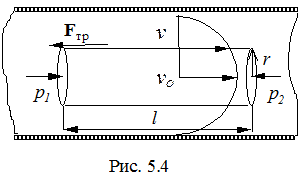При движении жидкости в круглой трубе ее скорость равна нулю у стенок трубы и максимальна на оси трубы. Полагая течение ламинарным, найдем, как меняется скорость в направлении радиуса трубы. Выделим в трубе воображаемый цилиндрический объем жидкости радиуса r и длины l, соосный с трубой (рис. 5.4). При стационарном течении жидкости сила трения F_тр равна разности сил давления:

F_тр=(p₁-p₂)p·r²=Dpp·r²,

где p₁ и p₂ - давления жидкости в сечении 1 и 2, Dp - разность давлений на концах объема, pr ² - площадь основания цилиндра. Подставляя сюда силу трения F_тр = - h(dv/dr)2p rl, получим Dppr ² = - h(dv/dr)2prl, где dv/dr - градиент скорости, h - коэффициент вязкости жидкости, 2prl - площадь боковой поверхности цилиндра. Разделяя переменные r и v, получим dv = - (Dp/2hl)rdr. Суммируя все изменения dv от r до R, придем к определенному интегралу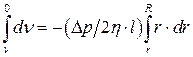, в котором учтено, что на стенках трубы при r = R скорость движения слоя v = 0. После интегрирования получим

v = ( D p/4hl)(R² - r²). (5.10)

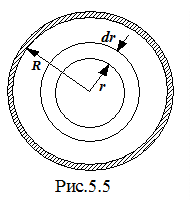Формула (5.10) показывает, что скорость частиц как функция расстояния от оси трубы изменяется по параболическому закону. Используя формулу (5.10), можно решить такую важную практическую задачу, как нахождение объема жидкости Q, протекающего через поперечное сечение трубы за единицу времени. Разобьем поперечное сечение трубы на кольца шириной dr (рис. 5.5). Через кольцо радиусом r за секунду пройдет объем жидкости, равный произведению площади кольца 2prdr на скорость течения в точках, находящихся на расстоянии r от оси трубы:

dQ = v2prdr. (5.11)

Чтобы получить поток Q, нужно просуммировать все dQ при изменении r от 0 до R. Получим определенный интеграл, который с учетом выражения (5.10), будет иметь вид

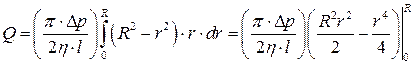
или

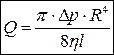. (5.12)

Это выражение называется формулой Пуазейля. Из формулы практический вывод, что для улучшения пропускной способности труб в первую очередь следует увеличить их радиус. Например, при увеличении радиуса трубы в 2 раза количество протекающей жидкости возрастет в 16 раз.

Формула (5.12) используется при определении вязкости жидкости. Измерив поток жидкости Q через капилляр известного радиуса и зная перепад давления, можно определить вязкость жидкости.

Дата добавления: 2013-12-12