Адиабатический процесс

Наряду с изопроцессами существует адиабатический процесс, широко распространенный в природе. Адиабатическим процессом называют процесс, протекающий без теплообмена с внешней средой. Это означает, что газ при адиабатическом процессе не получает извне тепла: dQ = 0. Первое начало термодинамики для моля газа будет иметь вид dU _m = - dA _m. С учетом выражений (10.4) и (10.9) запишем последнее равенство в виде

C _{v m} dT = -dA _m = - pdV _m. (10.14)

Если при адиабатическом процессе газ расширяется, то dA _m 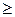0, dT 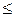0, т.е. внутренняя энергия газа уменьшается, температура также уменьшается, газ при адиабатическом расширении охлаждается. При адиабатическом сжатии газа dA _m 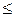0, dT 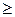0, его температура увеличивается. Молекулярно-кинетическое объяснение этого явления дано выше.

Примером адиабатического процесса является распространение звуковых колебаний в воздухе. Сжатия и разряжения воздуха происходят так часто, что тепло не успевает переходить от слоев, имеющих большую температуру, к слоям с меньшей температурой. Следовательно, процессы, происходящие достаточно быстро, близки к адиабатическим.

Важное значение адиабатический процесс имеет в объяснении атмосферных явлений. Слои воздуха, поднимающиеся вверх, расширяются, так как атмосферное давление уменьшается с высотой. За счет расширения газ адиабатически охлаждается, поэтому с увеличением высоты температура газа уменьшается. Это объясняет и тот факт, что ветер, дующий с гор, всегда кажется теплым, так как воздух, перемещаясь, сжимается, а ветер, дующий с моря, кажется прохладным.

При адиабатическом процессе газ подчиняется уравнению Клапейрона pV _m = RT. Наличие дополнительного условия (10.14) позволяет уменьшить в этом уравнении число параметров состояния. Для этого выразим p из уравнения Клапейрона и подставим его в формулу (10.14): C _{v m} dT = - RTdV _m /V _m. Разделяя переменные, получим dT/T +RdV _m /(V _m C _{v m} )= 0. Взяв неопределенный интеграл, получим ln T +(R/C _{v m} ) ln V_m = const. В согласии с (10.10) и (10.13) получим (R/C _{v m} ) = 2/i = g - 1 и с учетом последнего выражения ln T +(g - 1) ln V _m = const. Потенцируя это равенство, придем к уравнению

TV^g-1 = const, (10.15)

где индекс m опущен. Полученное соотношение представляет собой уравнение адиабаты в переменных T и V. Чтобы от этого уравнения перейти к уравнению с переменными p и V, выразим из уравнения Клапейрона-Менделеева температуру T = mpV/Rm и подставим ее в выражение (10.15).

Получим

pV^g = const. (10.16)

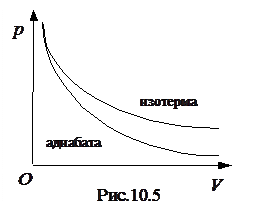
Соотношение (10.16) называют уравнением Пуассона. По форме это уравнение похоже на уравнение изотермы. Однако при увеличении объема для адиабатического процесса давление падает быстрее, чем для изотермического процесса (рис. 10.5).

Согласно выражению (10.14) работа для адиабатического процесса определится по формуле

A_m =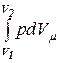= -= 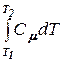С _m (T₁ - T₂).

С учетом выражения (10.10) получим для моля газа:

A _m = (i/2)R(T₁ - T₂) = (i/2)(p₁V_{1 m} - p₂V_{2 m}).

Для произвольной массы газа m получим A =(i /2)(m /m)(p₁V₁ - p₂V₂).

Дата добавления: 2013-12-12