Уравнение Ван-дер-Ваальса

Реальные газы

Поведение реальных газов при их малых плотностях хорошо описывается уравнением Клапейрона:

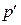
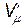= RT, (11.1)

где 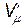- объем моля газа, 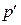- давление идеального газа, T - температура. Однако при давлениях порядка 200 атм. отклонение от уравнения (11.1) составляет около 5%. Это отклонение вызвано влиянием сил притяжения между молекулами и наличием собственного объема молекул. Для учета собственного объема молекул нидерландский физик Ван-дер-Ваальс ввел поправку b и представил объем, свободный для движения, в виде 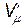= V_m - b. Уравнение (11.1) запишется в виде

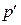(V_m - b) = RT, (11.2)

где V_m - объем моля реального газа.

Силы притяжения со стороны других молекул вызывают уменьшение скорости молекулы, соударяющейся со стенкой, поэтому силы взаимодействия молекул уменьшают давление газа на стенки сосуда на величину p_i . Давление реального газа запишется в виде p = 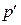- p_i и формула (11.2) будет иметь вид:

(p + p _i )·(V_m - b) = RT. (11.3)

Величина p_i зависит от объема газа. Если рассмотреть две половинки малого объема газа, то при увеличении количества молекул в них в n раз сила их взаимодействия f увеличится в n² раз (рис. 11.1). Следовательно, величина p_i ~ r ², где r - плотность газа. Учитывая, что при неизменной массе газа величина r обратно пропорциональна объему V, получим p_i = a / 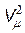. Выражение (11.3) запишется в виде

(p + a / 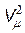)(V_m - b) = RT, (11.4)

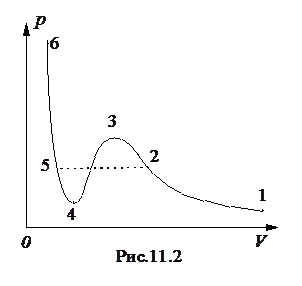где a - поправка Ван-дер-Ваальса, учитывающая притяжение молекул. Формулу (11.4.) называют уравнением Ван-дер-Ваальса. Это уравнение гораздо лучше согласуется с экспериментом, чем уравнение Клапейрона. Изотерма Ван-дер-Ваальса построена на рис. 11.2. Она отличается от изотермы идеального газа наличием S -образного участка 2-3-4-5, который обычно не реализуется на опыте. Если взять некоторый газ, состояние которого соответствует точке 1, и изотермически сжимать его, то уравнение Ван-дер-Ваальса на участке 1-2 будет хорошо описывать опытную кривую. При дальнейшем сжатии газа экспериментальная кривая пройдет по штриховой линии 2-5. В точке 2 газ является насыщенным паром, и при дальнейшем уменьшении его объема часть пара конденсируется. Система распадается на две фазы: жидкую и газообразную. Давление насыщенного пара является постоянным и линия 2-5 параллельна оси абсцисс. При уменьшении объема системы по линии 2-5 растет количество жидкой фазы, и в точке 5 насыщенный пар полностью конденсируется в жидкость. Жидкость является малосжимаемой, поэтому при дальнейшем уменьшении объема давление быстро возрастает. Участок 5-6 изотермы Ван-дер-Ваальса полностью совпадает с опытной кривой. S‑ образный участок изотермы, представляющий собой область неустойчивых состояний, на опыте обычно на реализуется. Участок 3-4 представляет собой область совершенно неустойчивых состояний и экспериментально его невозможно реализовать. При некоторых условиях, например, отсутствии центров конденсации или кипения, можно реализовать участки 2-3 и 4-5. Участок 2-3 соответствует перегретому пару, а участок 4-5 - перегретой или растянутой жидкости. Эти вполне устойчивые состояния называются метастабильными, и если искусственно ввести в метастабильную систему центры конденсации, то система скачком перейдет в двухфазное состояние. Воду можно перегреть на несколько десятков градусов, и если насыпать в нее немного мелкого песка, то происходит вскипание со взрывом. При перегонке многих жидкостей с целью очистки во избежание перегрева необходимо вводить специальные предметы в качестве центров кипения. Метастабильные состояния жидкости и пара широко используются при регистрации элементарных частиц.

Итак, уравнение Ван-дер-Ваальса позволило предсказать наличие неустойчивых состояний и неплохо количественно описать переход вещества из газообразного состояния в жидкое.

Дата добавления: 2013-12-12