Колебаний

Примерная схема решения задач по кинематике

Примеры решения задач по кинематике криволинейного движения

Задачи

Теория

Практическое занятие 2.

Задачи

Теория

Практическое занятие 1.

Соотношения (10.46) и (10.52) показывают, что энергия тела и его импульс зависят от системы отсчета, принятой в данном конкретном случае. Покажем, что величина

E²-P²c²

имеет одно и тоже значение во всех инерциальных системах отсчета. Воспользуемся указанными формулами и запишем:

,

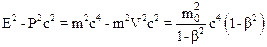или окончательно

.

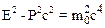Полученное соотношение позволяет записать полезные формулы:

,

.

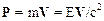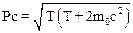Схема решения задач по кинематике

Записав условие задачи, сделать рисунок, на котором указать систему координат, изобразить траекторию движения точки. Отметить на рисунке кинематические характеристики движения: перемещение, скорость, ускорение. Если указывается, что на отдельных участках движение имеет различный характер, то необходимо рассматривать движение на каждом из них отдельно.

Установить связь между величинами, отмеченными на рисунке. Поскольку для решения системы уравнений и расчетов используется скалярная форма уравнений, то необходимо спроецировать входящие в уравнения векторы на оси выбранной системы координат. Полученную систему уравнений дополнить уравнениями, составленными на основе вспомогательных условий задачи и, проверив равенство количества уравнений и количества неизвестных, входящих в нее, решить систему кинематических уравнений относительно искомых величин.

Положение материальной точки в пространстве задается радиусом-вектором г:

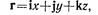где i, j, k — единичные векторы направлений (орты); х, у, z — координаты точки.

Кинематические уравнения движения в координатной форме:

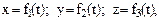
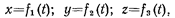
где t — время.

• Средняя скорость

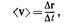
где 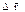— перемещение материальной точки за интервал времени .

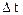Средняя путевая * скорость

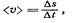
где 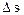— путь, пройденный точкой за интервал времени .

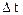Мгновенная скорость

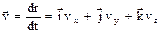
где 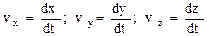— проекции скорости v на оси координат.

Модуль скорости

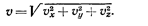
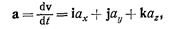• Ускорение

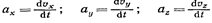
где проекции ускорения a на оси

координат.

Модуль ускорения

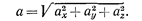
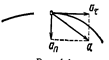
При криволинейном движении ускорение можно представить как сумму нормальной 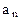и тангенциальной 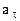составляющих (рис.1.1):

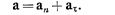
Модули этих ускорений:

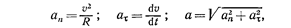
где R — радиус кривизны в данной точке траектории.

• Кинематическое уравнение равномерного движения материальной точки вдоль оси х

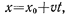
где 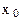— начальная координата; t — время. При равномерном движении

v =const и a=0.

• Кинематическое уравнение равнопеременного движения(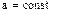)вдоль оси x

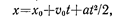
где v ₀ —начальная скорость; t — время.

Скорость точки при равнопеременном движении

v=v ₀+a t.

Примеры решения задач

Пример 1. Кинематическое уравнение движения материальной точки по прямой (ось х) имеет вид x=A+Bt+Ct³, где A=4 м, B=2 м/с, С=-0,5 м/с². Для момента времени t ₁=2 с определить:

1) координату x ₁ точки, 2) мгновенную скорость v ₁, 3) мгновенное ускорение a₁.

Решение. 1. Координату точки, для которой известно кинематическое уравнение движения, найдем, подставив в уравнение движения вместо t заданное значение времени t ₁:

x=A+Bt+Ct³.

Подставим в это выражение значения A, В, С, t ₁ и произведем вычисления:

X ₁=(4+4- 0,5 2³) м=4 м.

2. Мгновенную скорость в произвольный момент времени найдем, продифференцировав координату х по времени:.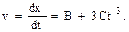

Тогда в заданный момент времени t ₁ мгновенная скорость

v ₁=B+3C t ₁² Подставим сюда значения В, С, t ₁ и произведем вычисления:

v ₁ =- 4 м/с.

Знак минус указывает на то, что в момент времени t₁=2 с точка движется в отрицательном направлении координатной оси.

3. Мгновенное ускорение в произвольный момент времени найдем, взяв вторую производную от координаты х по времени:

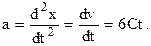
Мгновенное ускорение в заданный момент времени t ₁ равно a ₁ =6Ct ₁. Подставим значения С, t ₁и произведем вычисления:

a₁=(—6 0,5 2) м/с=—6 м/с.

Знак минус указывает на то, что направление вектора ускорения совпадает с отрицательным направлением координатной оси, причем в условиях данной задачи это имеет место для любого момента времени.

Пример 2. Кинематическое уравнение движения материальной точки по прямой (ось х) имеет вид, x=A+Bt+Ct², где A=5 м, B=4 м/с, С=-1 м/с². Построить график зависимости координаты х и пути s от времени. 2. Определить среднюю скорость < v_x > за интервал времени от t ₁=1 с до t ₂=6 с. 3. Найти среднюю путевую скорость < v > за тот же интервал времени.

Решение. 1. Для построения графика зависимости координаты точки от времени найдем характерные значения координаты — начальное и максимальное и моменты времени, соответствующие указанным координатам и координате, равной нулю.

Начальная координата соответствует моменту t =0. Ее значение равно

x₀=x | _{t= 0}=A=5 м.

Максимального значения координата достигает в тот момент, когда точка начинает двигаться обратно (скорость меняет знак). Этот момент времени найдем, приравняв нулю первую производную от координаты повремени:

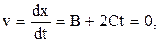, откуда t=—B/2C=2 с Максимальная координата

x _max =x / _{t =2} = 9 М.

Момент времени t, когда координата х=0, найдем из выражения x=A+Bt+Ct²=0.

Решим полученное квадратное уравнение относительно t:

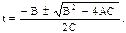
Подставим значения А, В, С и произведем вычисления:

t=(2±3) с.

Таким образом, получаем два значения времени: t'-=5 с и =-1 с. Второе значение времени отбрасываем, так как оно не удовлетворяет условию задачи (t>0).

График зависимости координаты точки от времени представляет собой кривую второго порядка. Для его построения необходимо иметь пять точек, так как уравнение кривой второго порядка со­держит пять коэффициентов. Поэтому кроме трех вычисленных ра­нее характерных значений координаты найдем еще два значения координаты, соответствующие моментам t ₁=l с и t ₂ =6 с:

x ₁ = А + Bt ₁ + Ct ₁² = 8 м, x ₂ = А + Bt ₂ + Ct ₂² = -7 м.

Полученные данные представим в виде таблицы:

Время, с Координата, м

t 1=0 x 0=A=5

t 1=1 x 0=8

t B=2 x max=9

=5 x =0

t 2=6 x 2=-7

Используя данные таблицы, чертим график зависимости координаты от времени (рис. 1.2).

График пути построим, исходя из следующих соображений:

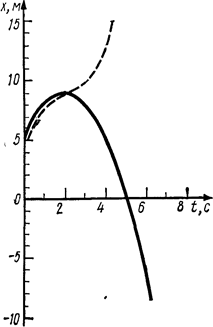
1) путь и координата до момента изменения знака скорости совпадают; 2) начиная с момента возврата (t _B) точки она движется в обратном направлении и, следовательно, координата ее убывает, а путь продолжает возрастать по тому же закону, по которому убывает координата.

Следовательно, график пути до момента времени t_B =2 с совпадает с графиком координаты, а начиная с этого момента яв­ляется зеркальным отображением графика координаты.

2. Средняя скорость < v _x> за интервал времени t₂—t₁ определяется выражением

<v_x>=(x₂-x₁)/(t₂—t₁).

Подставим значения x₁, x₂, t₁, t₂. из таблицы и произведем вычисления

< v_x >=(—7—8)/(6—1) м/с=—3 м/с.

3. Среднюю путевую скорость < v> находим из выражения

< v> =s/(t ₂- t₁),

где s — путь, пройденный точкой за интервал времени t₂.—t₁. Из графика на рис. 1.2 видно, что этот путь складывается из двух отрезков пути: S ₁ =x _max— x₁, который точка прошла за интервал времени t_B—t₁, и S₂= x _max+| x ₂|, который она прошла за интервал

Рис. 1.2

T ₂ —t _B. Таким образом, путь

S = S₁ + S₂ = (x _max— x ₂) + (x _max + | x ₂|) == 2 x _max + | x ₂|— x ₁.

Подставим в это выражение значения x _max, | x ₂|, x ₁ и произведем вычисления:

<s>=(2 9+7—8) м=17 м.

Тогда искомая средняя путевая скорость

< v >=17/(6—1) м=3,4 м.

Заметим, что средняя путевая скорость всегда положительна.

Прямолинейное движение

1.1. Две прямые дороги пересекаются под углом =60°. От перекрестка по ним удаляются машины: одна со скоростью v ₁ =60 км/ч, другая со скоростью v ₂= 80 км/ч.

Определить скорости v' и v", с которыми одна машина удаляется от другой. Перекресток машины прошли одновременно.

1.2. Точка двигалась в течение t ₁ = 15c со скоростью v ₁=5 м/с, в течение t ₂=10 с со скоростью v ₂ =8 м/с и в течение t ₃ =6 с со скоростью v ₃=20 м/с. Определить среднюю путевую скорость < v > точки.

1.3. Три четверти своего пути автомобиль прошел со скоростью v ₁=60 км/ч, остальную часть пути — со скоростью v ₂ =80 км/ч. Какова средняя путевая скорость < v > автомобиля?

1.4. Первую половину пути тело двигалось со скоростью v ₁=2 м/с, вторую — со скоростью v ₂=8 м/с. Определить среднюю путевую скорость < v >.

1.5. Тело прошло первую половину пути за время t ₁=2 с, вторую — за время t ₂=8 с. Определить среднюю путевую скорость < v > тела, если длина пути s=20 м.

1.6. -Зависимость скорости от времени для движения некоторого тела представлена на рис. 1.4. Определить среднюю путевую скорость < v > за время t =14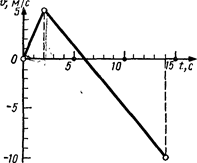

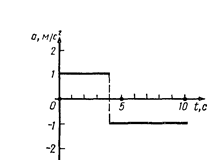
Рис. 1.5

1.7. Зависимость ускорения от времени при некотором движении тела представлена на рис. 1.5. Определить среднюю путевую скорость < v > за время t=8 с. Начальная скорость v ₀=0.

1.8. Уравнение прямолинейного движения имеет вид x=At+Bt², где A=3 м/с, B=—0,25 м/с². Построить графики зависимости координаты и пути от времени для заданного движения.

1.9. На рис. 1.5 дан график зависимости ускорения от времени для некоторого движения тела. Построить графики зависимости скорости и пути от времени для этого движения, если в начальный момент тело покоилось.

1.10. Движение материальной точки задано уравнением x=At+Bt², где A =4 м/с, В=— 0,05 м/с². Определить момент времени, в который скорость v точки равна нулю. Найти координату и ускорение в этот момент. Построить графики зависимости координаты, пути, скорости и ускорения этого движения от времени.

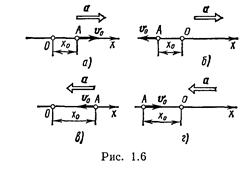
1.11. Написать кинематическое уравнение движения x=f(t) точки для четырех случаев, представленных на рис. 1.6. На каждой позиции рисунка — а, б, в, г — изображена координатная ось Ох, указаны начальные положение x ₀ и скорость v₀ материальной точки А, а также ее ускорение а.

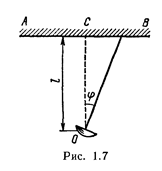
1.12. Прожектор О (рис. 1.7) установлен на расстоянии l ==100 м от стены АВ и бросает светлое пятно на эту стену. Прожектор вращается вокруг вертикальной оси, делая один оборот за время Т= 20 с. Найти: 1) уравнение движения светлого пятна по стене в течение первой четверти оборота; 2) скорость v, с которой светлое пятно движется по стене, в момент времени t=2 с. За начало отсчета принять момент, когда направление луча совпадает с ОС.

1.13. Рядом с поездом на одной линии с передними буферами паровоза стоит человек. В тот момент, когда поезд начал двигаться с ускорением а=0,1 м/с², человек начал идти в том же направлении со скоростью v =1,5 м/с. Через какое время t поезд догонит человека? Определить скорость v ₁ поезда в этот момент и путь, пройденный за это время человеком.

1.14. Из одного и того же места начали равноускоренно двигаться в одном направлении две точки, причем вторая начала свое движение через 2 с после первой. Первая точка двигалась с начальной скоростью v ₁==l м/с и ускорением a₁=2 м/с², вторая — с начальной скоростью v ₂=10 м/с и ускорением а₂=1 м/с². Через сколько времени и на каком расстоянии от исходного положения вторая точка догонит первую?

1.15. Движения двух материальных точек выражаются уравнениями:

x ₁ =A ₁ +B ₁t +C ₁ t², x ₂ =A ₂ +B ₂t +C ₂ t²,

где A ₁=20 м, A ₂=2 м, B ₁ =B ₂ =2 м/с, C₁= — 4 м/с², С₂=0,5 м/с².

В какой момент времени t скорости этих точек будут одинаковыми? Определить скорости v ₁ и v ₂ и ускорения a₁ и а₂ точек в этот момент:

1.16. Две материальные точки движутся согласно уравнениям;

x ₁ =A ₁ t+B ₁t² +C ₁ t ³, x ₂ =A ₂ t+B ₂t² +C ₂ t ³,

где A ₁=4 м/c, B ₁=8 м/с², C₁= — 16 м/с3, A ₂=2 м/с, B ₂ = - 4 м/с², С₂=1м/с³

В какой момент времени t ускорения этих точек будут одинаковы? Найти скорости v ₁ и v ₂ точек в этот момент.

1.17. С какой высоты Н упало тело, если последний метр своего пути оно прошло за время t =0,1 с?

1.18. Камень падает с высоты h=1200 м. Какой путь s пройдет камень за последнюю секунду своего падения?

1.19. Камень брошен вертикально вверх с начальной скоростью v ₀==20 м/с. По истечении какого времени камень будет находиться на высоте h=15м? Найти скорость v камня на этой высоте. Сопротивлением воздуха пренебречь. Принять g=10 м/с².

1.20. Вертикально вверх с начальной скоростью v ₀=20 м/с брошен камень. Через 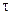=1 с после этого брошен вертикально вверх другой камень с такой же скоростью. На какой высоте h встретятся камни?

1.21. Тело, брошенное вертикально вверх, находилось на одной и той же высоте h=8,6 м два раза с интервалом 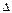t=3 с. Пренебрегая сопротивлением воздуха, вычислить начальную скорость брошенного тела.

1.22. С балкона бросили мячик вертикально вверх с начальной скоростью v ₀=5 м/с. Через t= 2 с мячик упал на землю. Определить высоту балкона над землей и скорость мячика в момент удара о землю.

1.23. Тело брошено с балкона вертикально вверх со скоростью v ₀=10 м/с. Высота балкона над поверхностью земли h=12,5 м. Написать уравнение движения и определить среднюю путевую скорость < v > с момента бросания до момента падения на землю.

1.24. Движение точки по прямой задано уравнением x=At+Bt², где A =2 м/с, В=— 0,5 м/с². Определить среднюю путевую скорость < v> движения точки в интервале времени от t ₁=l с до t ₂=3 с.

1.25. Точка движется по прямой согласно уравнению x=At+Bt³, где A=6 м/с, В == —0,125 м/с³. Определить среднюю путевую скорость < v> точки в интервале времени от t ₁=2 с до t ₂=6 с.

• Положение твердого тела (при заданной оси вращения) определяется углом поворота (или угловым перемещением) .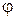

Кинематическое уравнение вращательного движения

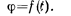
• Средняя угловая скорость

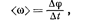
где 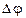— изменение угла поворота за интервал времени 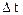. Мгновенная угловая скорость *

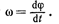
• Угловое ускорение *

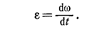
• Кинематическое уравнение равномерного вращения

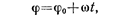
где 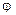—начальное угловое перемещение; t— время. При равномерном вращении 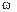=const и 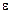=0.

*Угловая скорость и угловое ускорение являются аксиальными векторами, их направления совпадают с осью вращения.

· частотота вращения

n=N/t, или n=1/T,

где N — число оборотов, совершаемых телом за время t; Т — период вращения (время одного полного оборота).

• Кинематическое уравнение равнопеременного вращения (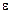= const.)

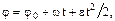
где 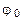—начальная угловая скорость; t— время.

Угловая скорость тела при равнопеременном вращении

.

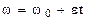• Связь между линейными и угловыми величинами, характеризующими вращение материальной точки, выражается следующими формулами:

путь, пройденный точкой по дуге окружности радиусом R,

s=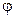R (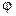— угол поворота тела);

скорость точки линейная

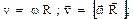
ускорение точки:

тангенциальное

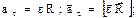
нормальное

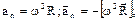
Пример 1. Автомобиль движется по закруглению шоссе, имеющему радиус кривизны R=50 м. Уравнение * движения автомобиля 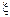(t) = A+Bt+Ct², где A=10 м, B=10 м/с, С=—0,5 м/с². Найти: 1) скорость v автомобиля, его тангенциальное 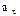, нормальное а _n. и полное а ускорения в момент времени t =5 с; 2) длину пути s и модуль перемещения |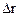| автомобиля за интервал времени 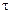=10 с, отсчитанный с момента начала движения.

Решение. 1. Зная уравнение движения, найдем скорость, взяв первую производную от координаты по времени:

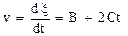. Подставим в это выражение значения В, С, t и произведем вычисления:

v =5 м/с.

Тангенциальное ускорение найдем, взяв первую производную от скорости по времени: 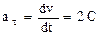Подставив значение С, получим 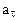= —1 м/с².

Нормальное ускорение определяется по формуле a_n= v ²/R. Подставим сюда найденное значение скорости и заданное значение радиуса кривизны траектории и произведем вычисления:

a_n==0,5 м/с².

Полное ускорение, как это видно из рис. 1.1, является геометрической суммой ускорений а и а _n: а = а 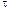+ а _n. Модуль ускорения 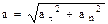. Подставив в это выражение найденные значения аи а_n получим

а=1,12 м/с².

2. Чтобы определить путь s, пройденный автомобилем, заметим, что в случае движения в одном направлении (как это имеет место в условиях данной задачи) длина пути s равна изменению криволинейной координаты 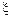т. е.

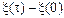s=, или .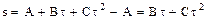

Подставим в полученное выражение значения В, С, 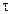и произведем вычисления:

s=50 м.

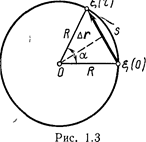
Модуль перемещения, как это видно из рис. 1.3, равен |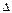r|=2Rsin(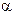/2),

где 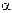— угол между радиусами-векторами, определяющими начальное 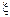(0) и конечное 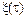положения автомашины на траектории. Этот угол (в радианах) находим как отношение длины пути s к радиусу кривизны R траектории, т. е. 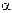= =s/R. Таким образом,

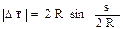
Подставим сюда значения R, s ипроизведем вычисления:

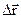|[= 47,9м.

Пример 4. Маховик, вращавшийся с постоянной частотой n₀=10 с¹, при торможении начал вращаться равнозамедленно. Когда торможение прекратилось, вращение маховика снова стало равномерным, но уже с частотой п=6 с¹. Определить угловое ускорение 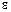маховика и продолжительность t торможения, если за время равнозамедленного движения маховик сделал N==50 оборотов.

Решение. Угловое ускорение маховика связано с начальной 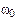и конечной 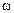угловыми скоростями соотношением 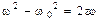, откуда 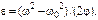Но так как 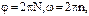то

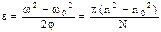
Подставив значения 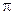, п, п ₀, N и вычислив, получим

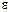=3,14(6²-10²)/50 рад/с²=—4,02 рад/с².

Знак минус указывает на то, что маховик вращался замедленно. Определим продолжительность торможения, используя формулу, связывающую угол поворота 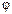со средней угловой скоростью < v> вращения и временем t: 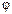=<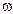>t. По условиям задачи, угловая скорость линейно зависит от времени и поэтому можно написать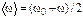, тогда ,

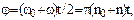Откуда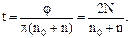

Подставив числовые значения и произведя вычисления, получим

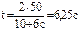
Криволинейное движение

1.26. Материальная точка движется по плоскости согласно уравнению r (t)= i At³+ j Bt². Написать зависимости: 1) v (t); 2) a (t).

1.27. Движение материальной точки задано уравнением r (t)=A (i cos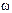 t - j sin 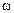t), где A =0,5 м, 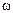=5 рад/с. Начертить траекторию точки. Определить модуль скорости | v | и модуль нормального ускорения |a_n |.

1.28. Движение материальной точки задано уравнением r (t) = i (A+Bt ² )+ j Ct, где A==10 м, В= — 5 м/с², С=10 м/с. Начертить траекторию точки. Найти выражения v (t) и a (t). Для момента времени t =1 с вычислить: 1) модуль скорости | v |; 2) модуль ускорения |а|; 3) модуль тангенциального ускорения | а 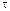|; 4) модуль нор­мального ускорения | a_n |.

1.29. Точка движется по кривой с постоянным тангенциальным ускорением a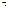=0,5 м/с². Определить полное ускорение а точки на участке кривой с радиусом кривизны R=3 м, если точка движется на этом участке со скоростью v ==2 м/с.

1.30. Точка движется по окружности радиусом R==4 м. Начальная скорость v ₀ точки равна 3 м/с, тангенциальное ускорение a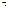=1 м/с². Для момента времени t=2 с определить: 1) длину пути s, пройденного точкой; 2) модуль перемещения |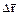|; 3) среднюю путевую скорость |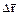|; 4) модуль вектора средней скорости |< v >|.

1.31. По окружности радиусом.R=5 м равномерно движется материальная точка со скоростью v =5 м/с. Построить графики зависимости длины пути s и модуля перемещения |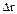| от времени t. В момент времени, принятый за начальный (t=0), s(0) и |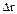(0)| считать равными нулю.

1.32. За время t=6 с точка прошла путь, равный половине длины окружности радиусом R==0,8 м. Определить среднюю путевую скорость < v > за это время и модуль вектора средней скорости |< v >|.

1.33. Движение точки по окружности радиусом R=4 м задано уравнением * 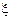= A+Bt+Ct², где A=10 м, В=—2 м/с, С=1 м/с². Найти тангенциальное а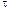, нормальное a_n и полное а ускорения точки в момент времени t =2с.

1.34. По дуге окружности радиусом R= 10 м движется точка. В некоторый момент времени нормальное ускорение точки а_n=4,9 м/с²; в этот момент векторы полного и нормального ускорений образуют угол 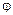=60°. Найти скорость v и тангенциальное ускорение a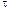точки.

1.35. Точка движется по окружности радиусом R=2 м согласно уравнению * 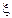= At³, где A =2 м/с³. В какой момент времени t нормальное ускорение а_n точки будет равно тангенциальному а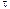. Определить полное ускорение а в этот момент.

1.36. Движение точки по кривой задано уравнениями x=A ₁ t³ и y =A₂ t, где A₁==l м/с³, A₂=2 м/с. Найти уравнение траектории точки, ее скорость v и полное ускорение а в момент времени t=0,8 с.

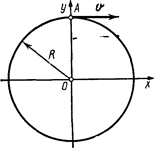
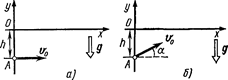
1.37. Точка А движется равномерно со скоростью v по окружности радиусом R. Начальное положение точки и направление движения указаны на рис. 1.8. Написать кинематическое уравнение движения проекции точки A на направление оси х.

1.38. Точка движется равномерно со скоростью v по окружности радиусом R и в момент времени, принятый за начальный (t=0), занимает положение, указанное на рис. 1.8. Написать кинематические уравнения движения точки: 1) в декартовой системе координат, расположив оси так, как это указано на рисунке; 2) в полярной системе координат (ось х считать полярной осью).

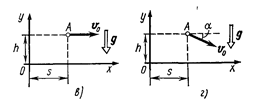
1.39. Написать для четырех случаев, представленных на рис. 1.9:

1) кинематические уравнения движения x=f ₁(t) и x=f ₂(t); 2) уравнение траектории у=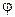(х). На каждой позиции рисунка — а, б, в, г — изображены координатные оси, указаны начальное положение точки A, ее начальная скорость v ₀ и ускорение g.

1.40. С вышки бросили камень в горизонтальном направлении.

Через промежуток времени t =2 с камень упал на землю на расстоянии s=40 м от основания вышки. Определить начальную v ₀ и конечную v скорости камня.

1.41. Тело, брошенное с башни в горизонтальном направлении со скоростью v =20 м/с, упало на землю на расстоянии s (от основания башни), вдвое большем высоты h башни. Найти высоту башни.

1.42. Пистолетная пуля пробила два вертикально закрепленных листа бумаги, расстояние l между которыми равно 30 м. Пробоина во втором листе оказалась на h=10см ниже, чем в первом. Определить скорость v пули, если к первому листу она подлетела, двигаясь горизонтально. Сопротивлением воздуха пренебречь.

1.43. Самолет, летевший на высоте h-=2940 м со скоростью v =360 км/ч, сбросил бомбу. За какое время t до прохождения над целью и на каком расстоянии s от нее должен самолет сбросить бомбу, чтобы попасть в цель? Сопротивлением воздуха пренебречь.

1.44. Тело брошено под некоторым углом 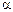к горизонту. Найти этот угол, если горизонтальная дальность s полета тела в четыре раза больше максимальной высоты Н траектории.

1.45. Миномет установлен под углом 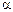=60° к горизонту на крыше здания, высота которого h=40 м. Начальная скорость v ₀ мины равна 50 м/с. Требуется: 1) написать кинематические уравнения движения и уравнения траектории и начертить эту траекторию с соблюдением масштаба; 2) определить время 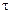полета мины, максимальную высоту Н ее подъема, горизонтальную дальность s полета, скорость v в момент падения мины на землю. Сопротивлением воздуха пренебречь.

Указание. Начало координат поместить на поверхности земли так, чтобы оно находилось на одной вертикали с минометом и чтобы вектор скорости v лежал в плоскости хОу.

1.46. Снаряд, выпущенный из орудия под углом 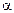=30° к горизонту, дважды был на одной и той же высоте h: спустя время t ₁=10 с и t ₂=50 с после выстрела.

Определить начальную скорость v ₀ и высоту h.

1.47. Пуля пущена с начальной скоростью v ₀=200 м/с под углом 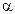=60° к горизонту. Определить максимальную высоту Н подъема, дальность s полета и радиус R кривизны траектории пули в ее наивысшей точке. Сопротивлением воздуха пренебречь.

1.48. Камень брошен с вышки в горизонтальном направлении с начальной скоростью v ₀=30 м/с. Определить скорость v, тангенциальное aи нормальное a_n ускорения камня в конце второй секунды после начала движения.

1.49. Тело брошено под углом 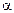=30° к горизонту. Найти тангенциальное a; и нормальное а_n ускорения в начальный момент движения.

Рис. 1.8 Рис. 1.9

Вращение тела вокруг неподвижной оси

1.50. Определить линейную скорость v и центростремительное ускорение a_n точек, лежащих на земной поверхности: 1) на экваторе; 2) на широте Москвы (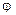=56°).

1.51. Линейная скорость v ₁ точек на окружности вращающегося диска равна 3 м/с. Точки, расположенные на 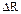=10 см ближе к оси, имеют линейную скорость v ₂=2 м/с. Определить частоту вращения п диска.

1.52. Два бумажных диска насажены на общую горизонтальную ось так, что плоскости их параллельны и отстоят на d=30 см друг от друга. Диски вращаются с частотой n==25 с^-1. Пуля, летевшая параллельно оси на расстоянии r=12 см от нее, пробила оба диска. Пробоины в дисках смещены друг относительно друга на расстоя-ние s==5 см, считая по дуге окружности. Найти среднюю путевую скорость < v > пули в промежутке между дисками и оценить создаваемое силой тяжести смещение пробоин в вертикальном направлении. Сопротивление воздуха не учитывать.

1.53. На цилиндр, который может вращаться около горизонтальной оси, намотана нить. К концу нити привязали грузик и предоставили ему возможность опускаться. Двигаясь равноускоренно, грузик за время t=3 с опустился на h= 1,5 м. Определить угловое ускорение 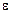цилиндра, если его радиус r=4 см.

1.54. Диск радиусом r = 10 см, находившийся в состоянии покоя, начал вращаться с постоянным угловым ускорением 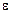=0,5 рад/с². Найти тангенциальное a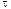, нормальное а_п и полное а ускорения точек на окружности диска в конце второй секунды после начала вращения.

1.55. Диск радиусом r=20 см вращается согласно уравнению 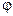=A+B t+Сt³, где A=3 рад, В=—1 рад/с, С=0,1 рад/с³. Определить тангенциальное a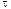нормальное а_n и полное а ускорения точек на окружности диска для момента времени t =10 с.

1.56. Маховик начал вращаться равноускоренно и за промежуток времени 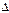t =10 с достиг частоты вращения n=300 мин"¹. Определить угловое ускорение 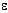маховика и число N оборотов, которое он сделал за это время.

1.57. Велосипедное колесо вращается с частотой п=5 с¹. Под действием сил трения оно остановилось через интервал времени 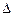t =1 мин. Определить угловое ускорение 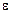и число N оборотов, которое сделает колесо за это время.

1.58. Колесо автомашины вращается равноускоренно. Сделав N=50 полных оборотов, оно изменило частоту вращения от n₁=4 с¹ до n₂==6 с¹. Определить угловое ускорение 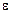колеса.

1.59. Диск вращается с угловым ускорением 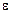=—2 рад/с². Сколько оборотов N сделает диск при изменении частоты вращения от n₁=240 мин ^-1 до n₂=90 мин ^-1? Найти время 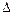t, в течение которого это произойдет.

1.60. Винт аэросаней вращается с частотой n=360 мин¹. Скорость v поступательного движения аэросаней равна 54 км/ч. С какой скоростью u движется один из концов винта, если радиус R винта равен 1 м?

1.61. На токарном станке протачивается вал диаметром d= 60 мм. Продольная подача h резца равна 0,5 мм за один оборот. Какова скорость v резания, если за интервал времени 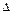t =1 мин протачивается участок вала длиной l =12 см?

Пример 1.1. Снаряд вылетел под углом a = 30⁰ к горизонту со скоростью V₀ = 200 м/с. Определить скорость снаряда, а также его нормальное и тангенциальное ускорения через t = 3 с после начала движения. На какое расстояние S переместится за это время снаряд по горизонтали, на какой высоте он окажется?

Решение

L=?, H=? аН=?, аt=?_________ V0=200 м/c, a=30°, g=9,8 м/с^2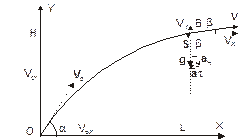

Выберем двухмерную систему координат X,Y и совместим ее начало с положением снаряда перед выстрелом. Изобразим траекторию движения снаряда кривой ОВ и предположим, что снаряд через три секунды полета находится в точке В. Так как движение снаряда происходит с постоянным ускорением g, сообщаемым силой тяжести, и начальная скорость снаряда V ₀ не равна нулю, то законы кинематики должны быть записаны так:

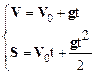, (1)

В проекциях на оси координат уравнения (1) имеют вид:

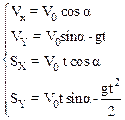
Величины V₀cos α; и V₀sin α равны проекциям начальной скорости на оси Х и Y, соответственно. Из ортогональности проекций V_x и V_y следует:

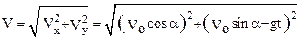(2)

Из чертежа видно, что проекции вектора перемещения S на оси координат равны горизонтальному L и вертикальному H перемещению снаряда: S_X=L и S_Y=H, поэтому

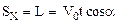(3)

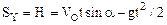(4)

Разлагая ускорение снаряда g в точке В на направления касательной и нормали к траектории, отметим его нормальную а _Н и тангенциальную а _τ составляющие. Из чертежа видно, что

а_н = g sinβ, α_τ = g cosβ, (5)

β – угол между вертикалью и нормалью к траектории в точке В. В параллелограммах скоростей и ускорений имеются равные углы b (как углы с перпендикулярными сторонами).

Тригонометрические функции угла β можно найти из разложения скорости снаряда в точке В:

,

.

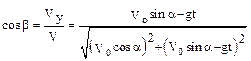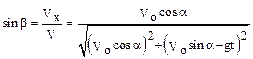Подставляя в соотношения (5) выражения для тригонометрических функций имеем окончательно:

,

.

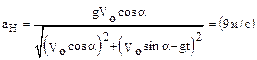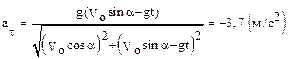Перемещение снаряда по горизонтали и его высоту находим по формулам (3) и (4):

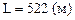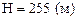, , L.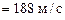

С помощью соотношения (2) найдем величину скорости снаряда после трех секунд полета:

V=188 (м/c)

Замечание. Отрицательное значение α_τ на третьей секунде полета показывает, что в этот момент скорость снаряда убывает, т. е. он еще находится на восходящей ветви параболы, например в точке В.

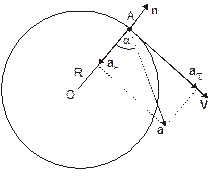
Пример 1.2. Диск радиусом R = 10 см находился в состоянии покоя, потом начал вращаться с постоянным угловым ускорением b=0,5 рад/с². Найти тангенциальное, нормальное и полное ускорение точек на окружности диска в конце второй секунды после начала вращения, а также угол, который составляет вектор полного ускорения любой точки диска с его радиусом.

a_H=?, a_t=?, а=?, a=?

R=10 см=0,1 м

b=0,5 с ^–2

t=2 c, w₀=0

Решение

Разложим вектор полного ускорения а точки на тангенциальное ускорение α _τ и нормальное ускорение а _н (n – вектор внешней нормали к траектории):

.

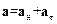Из рисунка видно, что tgα = α_τ/α_н. Используя связь линейных и угловых ускорений можно записать

α_τ = βR.

Известно, что нормальное ускорение определяется формулой:

,

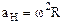где угловая скорость определяется из основного уравнения кинематики вращательного движения

.

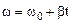По условию w₀ = 0, тогда .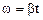

Следовательно,

а_Н = β² t²R.

Производя вычисления, получим:

α_τ = 0.510^-1= 5×10^-2 (м/с²); а_н = 25·10^-2 · 4·10^-2 =10^-2 (м/с²).

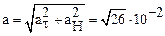(м/с²); 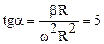, α =79°.

Решение задач этого раздела рекомендуется выполнять в следующем порядке:

· выбрать систему отсчета, взяв начало координат в положении равновесия материальной точки;

· записать начальные условия движения материальной точки;

· составить дифференциальное уравнение движения материальной точки в проекции на соответствующую ось;

· проинтегрировать дифференциальное уравнение движения, использовав начальные условия движения для определения постоянных интегрирования.

·

При составлении дифференциального уравнения движения надо изобразить материальную точку в промежуточном положении, соответствующем ее положительной координате, предположив при этом, что точка перемещается в сторону возрастания этой координаты.

Пример 1.3.

Материальная точка колеблется по закону 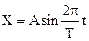. При значениях координаты Х₁ и Х₂ ее скорость равна V₁ и V₂. Определить амплитуду и период колебаний.

A=?, T=? Х1,V1 Х2, V2

Решение

Найдем скорость колеблющейся материальной точки. По определению скорости имеем:

.

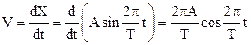Используя данные задачи, образуем систему уравнений:

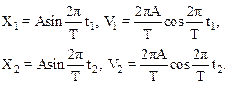
Выражая из полученных уравнений функции синуса и косинуса для моментов времени t₁ и t₂ и воспользовавшись тригонометрической единицей 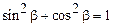, получим:

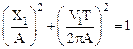и .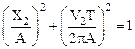

Решая систему, имеем:

,

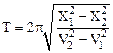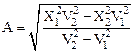
Задачи к главе I для самостоятельного решения

1.1. Две прямые дороги пересекаются под углом α = 60⁰. От перекрестка по ним удаляются машины: одна со скоростью V₁ = 60 км/ч, другая со скоростью V₂ = 80 км/ч. Определить скорости V' и V", с которыми одна машина удаляется от другой. Перекресток машины прошли одновременно.

V' = 122 κм/ч, V" = 72,2 км/ч.

1.2 Точка двигалась в течение t₁ = 15 с со скоростью V₁ = 5 м/с, в течение t₂ = 10 с со скоростью V₂ = 8 м/с и в течение t₃ = 6 с со скоростью V₃ = 20 м/с. Определить среднюю путевую скорость <V> точки.

<V> = 8,87 м/с.

1.3. Первую половину пути тело двигалось со скоростью V₁ = 2 м/с, вторую – со скоростью V₂ = 8 м/с. Определить среднюю путевую скорость <V>.

<V> = 2 V₁ V₂ /(V₁ + V₂ ) = 3,2 м/с.

1.4. Рядом с поездом на одной линии с передними буферами паровоза стоит человек. В тот момент, когда поезд начал двигаться с ускорением а = 0,1 м/с², человек начал идти в том же направлении со скоростью V = 1,5 м/с. Через какое время t поезд догонит человека? Определить скорость V₁ поезда в этот момент и путь, пройденный за это время человеком.

30 с; 3 м/с; 45 м.

1.5. Из одного и того же места начали равноускоренно двигаться в одном направлении две точки, причем вторая начала свое движение через 2 с после первой. Первая точка двигалась с начальной скоростью V₁ = 1 м/с и ускорением а₁ = 2 м/с², вторая – с начальной скоростью V₂ = 10 м/с и ускорением а₂ = 2 м/с². Через сколько времени и на каком расстоянии от исходного положения вторая точка догонит первую?

Встретятся дважды: через 3,4 с на расстоянии 15 м и через 10,6 с,

на расстоянии 123 м..

1.6. С какой высоты Н упало тело, если последний метр пути оно прошло за время t = 0,1 с?

Н = (2s + gt²)²/ (8gt²) = 5,61 м, где s = 1 м.

1.7. Камень падает с высоты h = 1200 м. Какой путь s пройдет камень за последнюю секунду своего падения?

S=150 м.

1.8. Камень брошен вертикально вверх с начальной скоростью V₀ = 20 м/с. По истечении какого времени камень будет находиться на высоте h = 15 м? Найти скорость V камня на этой высоте. Сопротивлением воздуха пренебречь. Принять g = 10 м/с².

м/с (при движении вверх); 3 с; -10 м/с (при падении).)

1.9. Точка движется по кривой с постоянным тангенциальным ускорением а_τ = 0,5 м/с². Определить полное ускорение а точки на участке кривой с радиусом кривизны R = 3 м, если точка движется на этом участке со скоростью V = 2 м/с.

а=1,42 м/с².

1.10. Точка движется по окружности радиусом R = 4 м. Начальная скорость V₀ точки равна 3 м/с, тангенциальное ускорение а_τ = 1 м/с². Для момента времени t = 2 c определить: 1) длину пути s, пройденного точкой; 2) модуль перемещения 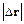; 3) среднюю путевую скорость <V>; 4) модуль вектора средней скорости .

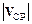1) 8 м; 2) 6,73 м; 3) 4 м/с; 4) 3,36 м/с.

1.11. По дуге окружности радиусом R = 10 м движется точка. В некоторый момент времени нормальное ускорение точки а_n = 4,9 м/с²; в этот момент векторы полного и нормального ускорений образуют угол a = 60⁰. Найти скорость V и тангенциальное ускорение а_τ точки.

8,5 м/с².

1.12. Точка движется по окружности радиусом R = 2 м согласно уравнению x= Аt³, где А = 2 м/с². В какой момент времени t нормальное ускорение а_n будет равно тангенциальному а_τ? Определить полное ускорение а в этот момент. В заданном уравнении движения ξ означает криволинейную координату, отсчитанную от некоторой начальной точки на окружности.

0,872 с; 14,8 м/с².

1.13. С вышки бросили камень в горизонтальном направлении. Через промежуток времени t = 2 c камень упал на землю на расстоянии s = 40 м от основания вышки. Определить начальную V₀ и конечную V скорости камня.

20 м/с; 28 м/с.

1.14. Пистолетная пуля пробила два вертикально закрепленных листа бумаги, расстояние L между которыми равно 30 м. Пробоина во втором листе оказалась на h =10 см ниже, чем в первом. Определить скорость V пули, если к первому листу она подлетела, двигаясь горизонтально. Сопротивлением воздуха пренебречь.

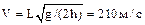
1.15. Тело брошено под некоторым углом α к горизонту. Найти этот угол, если горизонтальная дальность s полета тела в четыре раза больше максимальной высоты H траектории.

a=45⁰.

1.16. Тело брошено под углом α = 30° к горизонту. Найти тангенциальное а_τ и нормальное а_n ускорения в начальный момент движения.

4,9 м/с²; 8,55 м/с².

1.17. Линейная скорость V₁ точек на окружности вращающегося диска равна 3 м/с. Точки, расположенные на b = 10 см ближе к оси, имеют линейную скорость V₂ = 2 м/с. Определить частоту вращения n диска.

n = (V₁ - V₂) /(2πb) = 1,59 с^-1.

1.18. На цилиндр, который может вращаться около горизонтальной оси, намотана нить. К концу нити привязали грузик и предоставили ему возможность опускаться. Двигаясь равноускоренно, грузик за время t = 3 с опустился на h = 1,5 м. Определить угловое ускорение V цилиндра, если его радиус r =4 см.

ε = 2 h /(rt²) = 8,33 рад/с².

1.19. Маховик начал вращаться равноускоренно и за промежуток времени Dt = 10 с достиг частоты вращения n = 300 мин^-1. Определить угловое ускорение e маховика и число N оборотов, которое сделает колесо за это время.

ε = 2π n /(Δt) = 3,14 рад/с².

1.20. Частица колеблется по закону Х=Аcoswt. Построить графики: а) функций Х(t),X/dt, d²X/dt² в зависимости от t; b) функций dX/dt, d²X/dt² в зависимости от Х.

1.21. Частица совершает гармоническое колебание с амплитудой A и периодом T. Найти: а) время t₁, за которое положение частицы меняется от 0 до А/2; b) время t₂, за которое положение частицы меняется от А/2 до А.

t₁=T/12, t₂=T/6.

1.22. Шарик подвешен на длинной нити. Один раз его поднимают по вертикали до точки подвеса, другой раз его отклоняют как маятник на небольшой угол. В каком из этих случаев шарик скорее возвратится в начальное положение, если его отпустить?

В первом случае в 1,11 раз быстрее.

1.23. Частица совершает одномерные гармонические колебания около положения равновесия Х=0. Скорость ее меняется по закону 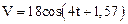см/с. найти путь, пройденный частицей за первые 10 секунд.

S=1,16 м.

1.24. Результирующее колебание точки, участвующей в двух колебаниях одного направления, описывается выражением 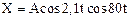. Найти период биений и циклические частоты w₁ и w₂ складываемых колебаний.

Т_Б=1,5 с, w₁=77,9 с ^–1 и w₂=82,1 с ^–1.

1.25. Частица одновременно участвует в двух взаимно перпендикулярных колебаниях, описываемых уравнениям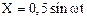и и 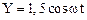. Найдите уравнение движения ч

Дата добавления: 2013-12-12