Решение задач по динамике колебаний

.

V2 = V,.

.

Из четвертого уравнения системы выразим скорость первого осколка после разрыва

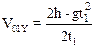(4)

Из последнего уравнения системы (3) выразим время полета второго осколка t₂:

.

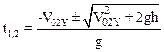Заметим, что время полета не может быть отрицательным, поэтому условию задачи удовлетворяет только один корень:

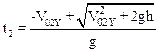(5)

Подставив время t₂ в шестое уравнение системы (3) найдем дальность L:

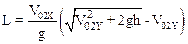(6)

Для определения проекции скорости V_02X воспользуемся законом сохранения импульса. Если рассматривать два состояния системы, в первом из которых система находится за мгновение до разрыва, а во втором – мгновение после разрыва, то при этом Dt®0 и импульс силы тяжести, действующий на систему мал, и ее импульс сохраняется. Можно записать:

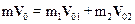, (7)

здесь m₁=m₂=m/2 – массы первого и второго осколков. Проецируя уравнение (7) на оси координат, получим систему уравнений:

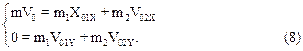
Из первого уравнения следует, что V_02X=2V₀. Подставляя найденное выражение в уравнение (6), получим для L

,

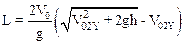где (как следует из второго уравнения системы (8)) V_02Y= - V_01Y, определенному соотношением (4).

Окончательно имеем:

.

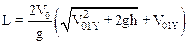Расчеты дают L=1600 м.

Пример 6.3.

Электропоезд, имеющий массу М, двигаясь под уклон из состояния покоя, за небольшой промежуток времени Dt приобрел скорость V. Угол наклона дороги по отношению к горизонту равен a, коэффициент трения равен m. Найти работу силы тяги. Сопротивлением воздуха пренебречь.

Решение

AF=? M Dt V0=0 V a m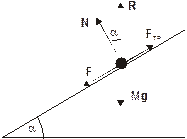

А. Решение этой задачи можно провести, используя определение работы:

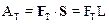(1)

Величины F_T и L найдем из системы кинематических уравнений

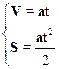
и уравнения движения электропоезда:

.

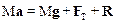Запишем уравнения системы в проекциях на оси координат:

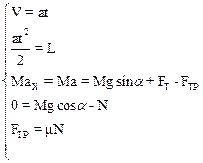
Решая систему, получим: для ускорения a=V/t, для пройденного пути L=Vt/2, для силы трения F_TP=mN=mMgcosa. Сила тяги равна

.

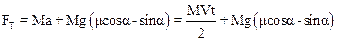Подставляя в формулу (1), окончательно получим:

.

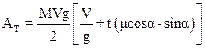В. Решение этой задачи можно провести, используя закон изменения механической энергии. При движении поезда его энергия изменяется так, что DЕ=А_ВНЕШ.

Энергия поезда Е₁ в начальном состоянии равна mgh₁, в конечном состоянии Е₂=mgh₂+mV²/2. Таким образом:

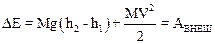. (1)

Работа внешних сил складывается из работы силы тяги и работы силы трения

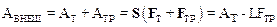, (2)

здесь L – пройденный при разгоне путь, F_T и F_TP численные значения силы тяги и трения.

Для определения неизвестных величин запишем систему уравнений

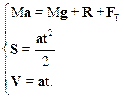
В проекции на оси координат она принимает вид

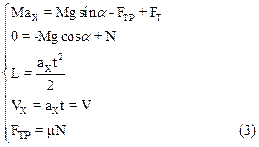
Из формулы (2) следует, что

,

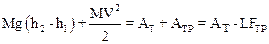откуда

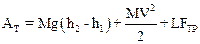(4)

Решая систему (3), найдем, что: a=V/t, L=Vt/2, h=h2-h1=-Lsina, F_TP=mN=mmgcosa.

Подставляя найденные выражения в (4), имеем окончательно для А_Т:

.

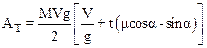Задачи к главе 6 для самостоятельного решения

6.1. Три лодки одинаковой массы M движутся по инерции друг за другом с одинаковой скоростью v. Из средней лодки в крайние одновременно перебрасы­вают грузы массой m со скоростью u относительно лодок. Какие скорости будут иметь лодки после перебрасывания? Сопротивление воды не учитывать.

6.2. Космический корабль должен, изменив курс, двигаться с прежним по модулю импульсом р под углом a к первоначальному направлению. На какое минимальное время должен быть включен двигатель с силой тяги F и как при этом нужно ориентировать ось двигателя?

t = 2p ·(sin a/2)/F, под углом b = (p + a)/2 к начальной скорости.

6.3. Космический корабль перед отделением последней ступени ракеты-носителя имел скорость v. После отбрасывания последней ступени его скорость стала равной 1,01v, при этом отделившаяся ступень удаляется относительно ко­рабля со скоростью 0,04v. Какова масса последней ступени, если масса корабля равна m0?

m = m0/3.

6.4. Граната, летевшая со скоростью 10 м/с, разорвалась на два осколка. Больший осколок, масса которого 60% массы всей гранаты, продолжал двигаться в прежнем направлении, но с увеличенной скоростью, равной 25 м/с. Найти скорость меньшего осколка.

v2 = 12,5 м/с.

6.5. Тело массой m соскальзывает с наклонной плоскости на неподвиж­ную платформу. Какую скорость будет иметь платформа, когда груз упадет на нее? Масса платформы M, высота начального положения тела h, угол наклона плоскости к горизонту a, коэффициент трения между наклонной плоскостью и телом k. Платформа движется без трения.

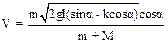
6.6. Плот массой М = 2000 кг находится на расстоянии s = 2 м от берега. Автомобиль массой m = 1000 кг перемещается от одного края плота к другому. Сможет ли при этом плот пристать к берегу, если длина плота L = 7 м.

Сможет.

6.7. На конце соломинки, лежащей на гладком столе, сидит кузнечик. С какой минимальной скоростью он должен прыгнуть, чтобы попасть на другой конец соломинки? Трение между столом и соломинкой не учитывать. Масса соломинки М, ее длина L, масса кузнечика m.

6.8. Снаряд массой m1 = 20 кг, летевший со скоростью v1 = 500 м/с под углом a = 30° к горизонту, попадает в платформу с песком массой m2 = 10 т и застревает в песке. Определите скорость движения платформы, если первона­чально платформа двигалась навстречу снаряду со скоростью v2 = 2 м/с.

v = 1,5 м/с.

6.9. Тело массой m = 1кг, брошенное с вышки в горизонтальном направлении со скоростью v₀ = 20м/с через t = 3с упало на землю. Определить кинетическую энергию Т, которую имело тело в момент удара о землю. Сопротивлением воздуха пренебречь.

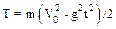= 633 Дж.

6.10. Насос выбрасывает струю воды диаметром d = 2 см со скоростью V = 20 м/с. Найти мощность N, необходимую для выбрасывания воды.

N=πρd²V³/8 = 1,26 кВт (ρ – плотность воды)

6.11. Какова мощность N воздушного потока сечением S = 0,55 м² при скорости воздуха V=20м/с и нормальных условиях?

N = ½ρSV³ = 2,84 кВт (ρ – плотность воздуха).

6.12. С какой наименьшей высоты h должен начать скатываться акробат на велосипеде (не работая ногами), чтобы поехать по дорожке, имеющей форму "мертвой петли" радиусом R = 4 м, и не оторваться от дорожки в верхней точке петли? Трением пренебречь.

h = 5R/2 = 10 м.

6.13. Конькобежец, стоя на льду, бросил вперед гирю массой m₁ = 5кг и вследствие отдачи покатился назад со скоростью V = 1м/c. Масса конькобежца m₂ = 60 кг. Определить работу А, совершенную конькобежцем при бросании гири.

390 Дж.

6.14. На рельсах стоит платформа, на которой закреплено орудие без противооткатного устройства так, что ствол его расположен в горизонтальном положении. Из орудия производят выстрел вдоль железнодорожного пути. Масса m₁ снаряда равна 10кг, и его скорость V₂ = 1км/с. На какое расстояние L откатится платформа после выстрела, если коэффициент сопротивления f = 0,002?

.

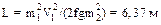6.15. Со шкива диаметром d = 0.48 м через ремень передается мощность N = 9 кВт. Шкив вращается с частотой n = 240 мин^-1. Сила натяжения Т₁ ведущей ветви ремня в 2 раза больше силы натяжения Т₂ ведомой ветви. Найти силы натяжения обеих ветвей ремня.

Т₁ = 2N/(πnd) = 2,98 кН; Т₂ = N/(πnd) = 1,49 кН.

6.16. Кинетическая энергия Т вращающегося маховика равна 1 кДж. Под действием постоянного тормозящего момента маховик начал вращаться разно замедленно и, сделав N = 80 оборотов, остановился. Определить момент М силы торможения.

M = T/(2πN) = 1,99 H×м.

6.17. Тело массы m бросили под углом a с начальной скоростью V₀. Найти среднюю мощность, развиваемую силой тяжести за все время движения тела, и мгновенную мощность этой силы как функцию времени.

<Р> = 0, Р = mg(gt-V₀sinα).

6.18. В системе отсчета, вращающейся вокруг неподвижной оси с постоянной угловой скоростью w = 5,0 рад/с, движется небольшое тело массы m = 100 г. Какую работу совершила центробежная сила инерции при перемещении этого тела по произвольному пути из точки 1 в точку 2, которые расположены на расстояниях r₁ = 30 см и r₂ = 50 см от оси вращения?

А = ½mω²(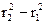) = 0,20 Дж.

6.19. Небольшая шайба массы m без начальной скорости соскальзывает с гладкой горки высотой h и попадает на доску массы M, лежащую у основания горки на гладкой горизонтальной плоскости. Вследствие трения между шайбой и доской шайба тормозится и, начиная с некоторого момента, движется вместе с доской как единое целое. Найти суммарную работу сил трения в этом процессе.

А = – μgh, где μ = mM/(m+M).

6.20. Парашютист массой m = 70 кг совершает затяжной прыжок и через t = 14 с имеет скорость V = 60 м/с. Считая движение парашютиста равноускоренным, найти работу по преодолению сопротивления воздуха.

.

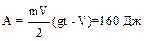6.21. Какую мощность должен развивать трактор при перемещении прицепа массой т = 5·10³ кг вверх по уклону со скоростью V = 1,0 м/с, если угол наклона α = 20°, а коэффициент трения прицепа μ = 0,20?

N = mgV(sinα+μcosα) = 26 кВт.

6.22. Пуля массой m ударяется о баллистический маятник массой М и застревает в нем. Какая доля кинетической энергии пули перейдет в теплоту?

.

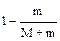6.23. Какая энергия пошла на деформацию двух столкнувшихся шаров массами m₁ = m₂ = 4,0 кг, если они двигались навстречу друг другу со скоростями V₁ = 3,0 м/с и V₂ = 8,0 м/с, а удар был прямой неупругий?

ΔЕ = m₁m₂(V₁+V₂)²/2(m₁+m₂) = 120 Дж.

6.24. Шар скатывается по наклонной плоскости с углом наклона a=30°. Какую скорость будет иметь центр шара относительно наклонной плоскости через 1,5 с, если его начальная скорость была равна нулю?

V = 5/7×(gtsinα) = 5,2 м/с.

6.25. Найти полезную мощность двигателя, приводящего в движение платформу в виде диска массой m₁ = 280 кг и радиусом R = 1,0 м, на краю которой стоит человек массой m₂ = 60 кг, если за t = 30 с платформа приобретает скорость, соответствующую частоте n = 1,2 об/с.

.

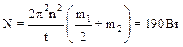6.26. Диск массой m₁ = 5 кг и радиусом R = 5 см, вращающийся с частотой n = 10 об/мин, приводится в сцепление с неподвижным диском массой m₂ = 10 кг такого же радиуса. Определить энергию, которая пойдет на нагревание дисков, если при их сцеплении скольжение отсутствует.

ΔΕ = 2π²n²R²m₁m₂/(m₁+m₂) =16 Дж.

Пример 7.1.

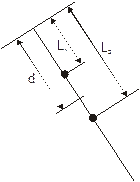
Маятник представляет собой невесомый стержень, на котором закреплены два небольших одинаковых груза – один на расстоянии L₁ = 15 см, другой на расстоянии L₂ = 30 см от точки подвеса. Определить период колебаний маятника.

T =?

L₁ = 15 см, L₂ = 30 см

Решение.

Период колебаний физического маятника определяется формулой:

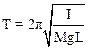, (1)

где M – масса маятника, I – его момент инерции, L – расстояние от точки подвеса до центра масс маятника. Выразим величины, определяющие величину периода.

Пренебрегая массой стержня, получим, что M = 2m, момент инерции маятника, как аддитивная величина, равен:

.

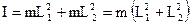Расстояние L найдем, используя определение центра масс:

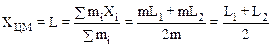. (2)

Подставляя найденные величины в (1), получим:

.

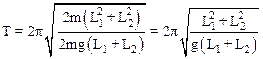Численные вычисления дают Т» 1 с.

Пример 7.2.

Пружинный маятник, колеблющийся в жидкой среде, в течение 50 секунд потерял 0,6 своей начальной энергии. Определить коэффициент сопротивления, если масса маятника 5 г.

r =?

t = 50 c, m = 5 г = 5×10 ^–3 кг, DЕ = Е₀ – Е = 0,6Е₀, или E/E₀ = 0,4

Решение.

Колебания маятника в жидкой среде (с трением) описываются уравнением:

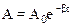, где b = r/m. (2)

Полная энергия маятника пропорциональна квадрату амплитуды:

,

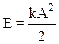здесь k – коэффициент жесткости пружины.

Зависимость полной энергии маятника от времени имеет вид:

.

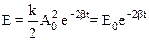По условию Е=0,4Е₀. Тогда

.

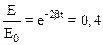Учитывая (2), имеем:

,

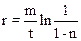откуда

r»9,16×10 ^–5 кг×с ^–1.

Пример 7.3.

Груз массой m = 10 кг, подвешенный к концу пружины, движется в жидкости. Коэффициент жесткости пружины с = 10 Н/см. Сила сопротивления движению R пропорциональна первой степени скорости груза: R = bV, где b = 1,6 H с/см. Найти закон движения груза, если в начальный момент груз был смещен из положения статического равновесия вниз на 4 см, и ему была сообщена вниз начальная скорость V₀ = 4 см/с.

х = х(t)

F_ТР=rV, m=10 кг, k=10 Н/cм=10 ³ Н/м, r=1,6 Н/см=1,6×10³ Н/м,

х₀=4 см=4×10^–2 м, V₀=4 cм/с=4×10^–2 м/c.

Решение

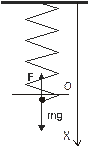
Движение груза описывается уравнением (7.22)

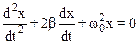, (1)

где 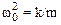, b=r/2m.

Подставив числовые значения, находим, что w₀=10 рад/с, b=8 рад/с; таким образом, b<w, и в задаче рассматривается случай малого сопротивления (см. (7.4)).

Закон движения груза имеет вид:

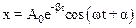, (2)

частота колебаний равна .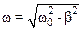

Для определения постоянных А₀ и a воспользуемся начальными условиями:

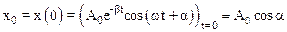, (3)

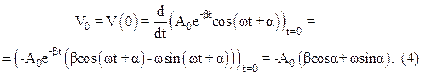Выразим из (3) А₀ и подставим в (4). Имеем:

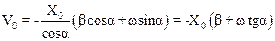(5)

Формула (5) позволяет получить выражение для a:

.

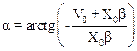Таким образом, искомое уравнение движения маятника имеет следующий вид:

.

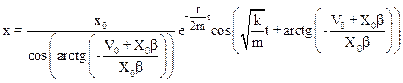Используя найденные ранее w₀=10 рад/с, b=8 рад/с и начальные значения х₀ и V₀ находим: a=0,59 рад и w=6 рад/с.

Итак, груз совершает затухающие колебания по закону:

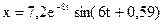×10^–2 м. (6)

Задачи к главе семь для самостоятельного решения

7.1. Найти закон, по которому меняется натяжение F нити математического маятника, совершающего колебания по закону j=j_mcoswt. Масса маятника m, длина – L.

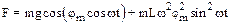
7.2. За 1 секунду амплитуда свободных колебаний уменьшается в два раза. В течение какого времени амплитуда уменьшится в 10 раз?

t=3,3 с.

7.3. Шар массой M=2,00 кг подвешен к двум соединенным последовательно пружинам. Коэффициенты эесткости пружин равны k₁=1000 Н/м и k₂=3000 Н/м. Пренебрегая массами пружин и трением найти: а) частоту малых колебаний шара, b) амплитуду колебаний, возникающих в случае, если шар установить на уровне, при котором пружины не напряжены, и отпустить без толчка.

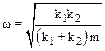, А=26 мм.

7.4. При неизменной вынуждающей силе амплитуда вынужденных колебаний при частотах w₁=100 с^–1 и w₂=300 с^–1 оказывается одинаковой. Найти резонансную частоту w_РЕЗ.

w_РЕЗ=224 с^–1.

7.5. Шарик катается по дну сферической чашки. Предполагая, что эти колебания можно считать сунусоидальными, определить их период.

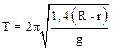
7.6. На каком расстоянии от центра нужно подвесить тонкий стержень длиной L, чтобы получить физический маятник, колеблющийся с максимальной частотой? Чему равна эта частота?

, .

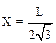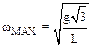7.7. Однородный диск радиусом r совершает малые колебания относительно горизонтальной оси, перпендикулярной плоскости диска и проходящей на расстоянии а от его центра. Чему равен период колебаний диска?

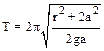
7.8. Блок (см. рис.) представляет собой сплошной цилиндр, который может вращаться вокруг своей оси без ощутимого трения. Масса блока М=5,0 кг, радиус R=10,0 см. Коэффициент жесткости пружины k=10^3 Н/м. Массой пружины и шнура можно пренебречь, проскальзывание шнура отсутствует. Масса груза m=1,0 кг. Определить частоту малых колебаний груза m.

w=16,9 с ^–1.

Пример 8.1.

Определить период колебаний математического маятника длиной L, точка подвеса которого опускается с ускорением w.

Решение

T=? ____ L, g, w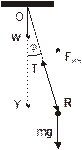

Запишем уравнение движения маятника в системе отсчета, связанной с ускоренно движущимся подвесом:

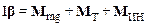. (1)

Проецируя уравнение (1) на вертикальную ось координат, имеем:

.

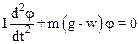Решение этого уравнения аналогично решению уравнения (7.11) и имеет вид:

.

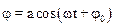Циклическая частота колебаний маятника равна:

.

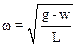Полученный результат говорит о том, что под влиянием силы инерции происходит изменение периода колебаний математического маятника.

Пример 8.2.

Цилиндр массой m и радиусом R упирается в ступеньку высотой h. С каким наибольшим ускорением можно двигать подставку, чтобы цилиндр не перекатился через упор?

a=? _____ m R h g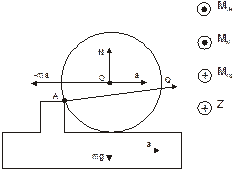

Решение

Цилиндр находится в покое относительно ускоренно движущегося основания. Отсутствию вращения относительно точки А соответствует равенство нулю результирующего вращательного момента сил, действующих на цилиндр. Выберем СО, жестко связанную с основанием и покажем силы, действующие на цилиндр: m g – сила тяжести, N – реакция горизонтального основания, Q –реакция ступеньки, m a – сила инерции.

При отсутствии вращения цилиндра относительно полюса О выполнено следующее условие:

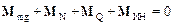, (1)

где момент силы Q равен нулю.

В проекции на ось Z уравнение (1) запишется так:

.

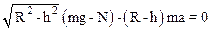Выразим N:

.

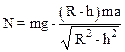Вращение цилиндра не начнется, если N>0:

.

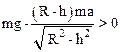Из последнего соотношения следует, что

,

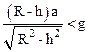или

.

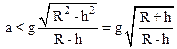Задачи к главе 9 для самостоятельного решения

9.1. Определить натяжение нити, связывающей два шарика объемом V=10см³ каждый, если верхний шарик плавает, наполовину погрузившись в воду. Нижний шарик в три раза тяжелее верхнего? Плотность воды ρ=1000 кг/м³.

F_нат=ρg V / 8.

9.2. Два шарика радиусами r₁ и r₂сделаны из материала плотностью ρ₁ и ρ₂ и соединены невесомым стержнем длиной l. Затем вся система помещена в жидкость плотностью ρ (ρ < ρ₁ и ρ < ρ₂). В какой точке стержня нужно прикрепить подвес, чтобы вся система находилась в равновесии при горизонтальном положении стержня?

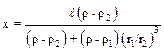от шара плотностью r₁.

9.3. В сообщающиеся сосуды диаметрами D₁и D₂ налита вода. Как изменится уровень воды в сосудах, если положить кусок дерева массой m в первый сосуд? Во второй сосуд? Плотность воды r.

_.

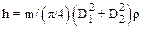9.4. В сосуд с водой опущена длинная трубка сечением S = 2см². В трубку налито m=72 г масла (ρ_м = 900 кг/м³).Плотность воды ρ_В = 1000 кг/м³. Найти разность уровней масла и воды.

Δh = m (ρ_в - ρ_м) / S ρ_в ρ_м.

9.5. При подъеме груза массой m = 2000 кг с помощью гидравлического пресса совершена работа А= 40 Дж. При этом малый поршень сделал n= 0 ходов, перемещаясь за один ход на h = 10 см. Во сколько раз площадь большого поршня больше площади малого?

S₂/S₁ = nhmg /A.

9.6. Из воды с глубины h₁=7 м кран поднимает чугунную плиту массой m=1400 кг. Найти совершенную работу, если плита была поднята на высоту h₂=5 м над водой. Плотность чугуна 7000 кг/м³. Считать g=10 м/с². Плотность воды ρ_в известна.

А = mg[ h₁(1- ρ_ч /ρ_в) + h₂ ].

9.7. Полый шар (внешний радиус R₁, внутренний R₂), сделанный из материала плотностью r₁, плавает на поверхности жидкости плотностью r₂. Какова должна быть плотность rвещества, которым следует заполнить внутреннюю полость шара, чтобы он находился в безразличном равновесии внутри жидкости?

r = [R₁³ (r₂ - r₁) + R₂³ r₁] (1 / R₂³).

9.8. Один конец нити закреплен на дне, а второй прикреплен к пробковому поплавку. При этом 0,75 всего объема поплавка погружено в воду с плотностью ρ_в. Определить силу натяжения нити, если масса поплавка m= 2 кг и плотность пробки r_п = 250 кг/м³. Массой нити пренебречь.

T = mg (3ρ_в /4r_п - 1).

9.9. Шарик всплывает с постоянной скоростью в жидкости, плотность которой в 4 раза больше плотности материала шарика. Определить силу сопротивления F жидкости при движении в ней шарика, считая ее постоянной. Масса шарика m=10 г.

F=3mg.

9.10. В цилиндрический сосуд налита ртуть и поверх ртути масло. Масса масла в 2 раза меньше массы ртути. Сосуд заполнен до высоты h=30 см. Определить давление на дно сосуда, если плотность ртути r_р=1,36 ×10⁴ кг/м³, а плотность масла r_м=900 кг/м³.

P=3r_мr_рgh/(r_р+2r_м).

9.11. С какой скоростью вытекает вода из узкого отверстия в дне бака, наполненного до высоты h=4,6 м? Вязкость не учитывать.

.

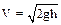Пример 10.1.

На космическом корабле-спутнике находятся часы, синхронизированные до полета с земными. Скорость V₀ спутника составляет 7,9 км/с. На сколько отстанут часы на спутнике по измерениям земного наблюдателя по своим часам за время 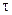₀=0,5 года.

Dt-?

_____________________

V₀=7,9 км/ч=7,9·10³ м/с,

t₀=0,5 года=15768000 с.

Решение.

Очевидно, что релятивистское замедление хода часов Dt=t-t₀, где t – время в системе отсчета К’, движущейся вместе со спутником со скоростью V₀ относительно "неподвижной" системы отсчета К, связанной с Землей. Так как (см.) местное время t на спутнике равно

,

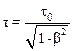то:

.

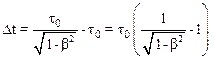Для нахождения времени запаздывания Dt можно воспользоваться следующим приближением:

.

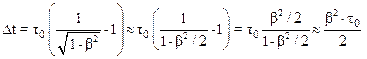Подставляя численные значения, имеем:

.

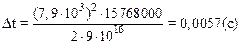Пример 10.2.

Предположим, что мы можем измерить длину стержня с точностью 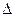L=0,1 мкм. При какой относительной скорости U двух инерциальных систем отсчета можно было бы обнаружить релятивистское сокращение длины стержня, собственная длина L₀ которого равна 1 м.

U-?

_______________

DL = 0,1 мкм=10^–7 м,

L₀ = 1 м.

Решение.

В соответствии с формулой (10.26) для Лоренцевского сокращения длины запишем:

,

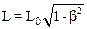где введено обозначение b=U/c.

Релятивистское сокращение длины можно было бы обнаружить при условии, что

,

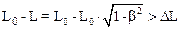или

. (*)

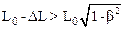Разрешая соотношение (*) относительно b получим:

.

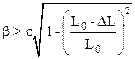Проводя преобразования и опуская малую величину (DL)² имеем для U выражение:

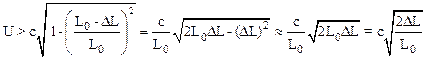Подставляя численные значения, имеем:

U=13,4·10⁴ м/с.

Пример 10.3.

Ускоритель сообщил радиоактивному ядру скорость V₁=0,4/с. В момент вылета из ускорителя ядро выбросило в направлении своего движения β-частицу со скоростью V₂=0,75 с относительно ускорителя. Найти скорость U₂₁ частицы относительно ядра.

U₂₁ –?

__________

V₁=0,4 с,

V₂=0,75 с

с=3×10⁸ м/с.

Решение

Релятивистское сложение скоростей осуществляется по закону (10.30):

. (*)

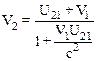Из формулы (*) следует, что

.

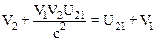В результате последовательных преобразовании имеем:

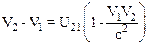
и

.

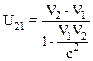Подставив численные значения, получим

.

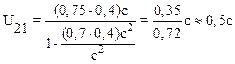Задачи к главе 10 для самостоятельного решения

10.1. Предположим, что мы можем измерить длину стержня с точностью 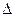L = 0,1 мкм. При какой относительной скорости U двух инерциальных систем отсчета можно было бы обнаружить релятивистское сокращение длины стержня, собственная длина L₀ которого равна 1 м.

10.3. На космическом корабле-спутнике находятся часы, синхронизированные до полета с земными часами. Скорость V₀ спутника составляет 7,9 км/с. На сколько отстанут часы на спутнике по измерениям земного наблюдателя по своим часам за время 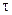₀=0,5 года.

10.4. Две релятивистские частицы движутся в лабораторной системе отсчета со скоростями V₁=0,6c и V₂=0,9с вдоль одной прямой. Определить их относительную скорость U₁₂ в двух случаях: 1) частицы движутся в одном направлении; 2) частицы движутся в противоположных направлениях.

10.5. Два ускорителя выбрасывают навстречу друг другу частицы со скоростями V=0,9 с. Определить относительную скорость U₁₂ сближения частиц в системе отсчета, движущейся вместе с одной из частиц.

10.6. С какой скоростью V движется частица, если ее релятивистская масса в три раза больше массы покоя.

10.7. Электрон движется со скоростью V=0,6c. Определить релятивистский импульс р электрона.

10.8. В лабораторной системе отсчета находятся две частицы. Одна частица с массой покоя 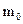движется со скоростью V=0,6c, другая с массой покоя 2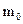покоится. Определить скорость V_c центра масс системы частиц.

10.9. Известно, что объем воды в океане равен 1,37×10⁹ км³. Определить, на сколько возрастет масса воды в океане, если температура воды повысится на 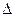t=1⁰C. Плотность 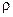воды в океане принять равной 1,03×10³ кг/м³.

10.10. Солнечная постоянная С (плотность потока энергии электромагнитного излучения Солнца на расстоянии, равном среднему расстоянию от Земли до Солнца) равна 1,4 кВт/м². 1. Определить массу, которую теряет Солнце в течение одного года. 2. На сколько изменится масса воды в океане за один год, если предположить, что поглощается 50 % падающей на поверхность океана энергии излучения? При расчетах принять площадь S поверхности океана равной 3,6×10⁸ км².

10.11. При какой скорости V кинетическая энергия любой частицы вещества равна ее энергии покоя?

10.12. Кинетическая энергия релятивистской частицы равна ее энергии покоя. Во сколько раз возрастет импульс частицы, если ее кинетическая энергия увеличится в n=4 раза?

Литература:

Учебники.

Гершензон Е. М, Малов Н. Курс общей физики. Механика. – М.: Просвещение, 1979.

Иродов И. Е. Основные законы механики. – М.: Высшая школа, 1985.

Савельев И. В. Курс общей физики. В 5 кн. Кн. I. Механика. Учебное пособие для втузов / И. В. Савельев. – М.: ООО «Издательство Астрель», 2002.

Сивухин Д. В. Общий курс физики. Т. 1. Механика. – М.: Наука, 1974.

Задачники.

Волькенштейн В. С. Сборник задач по общему курсу физики.

– М.: Наука, 1979. 10-е изд., перераб.

Сборник вопросов и задач по общей физике /Е. Г. Гершензона. – М.: Академия, 1999.

Чертов А. Г., Воробьев А. А. Задачник по физике. – М.: Физматлит, 2003. 7-е изд., перераб. и доп.

[1] В высшей математике обосновывается, что угол представляет собой векторную величину.

[2] В действительности колеблются не только частицы, расположенные на оси, а совокупность частиц в некотором объеме. При распространении плоской волны вдоль оси х все частицы среды, имеющие одну и ту же равновесную координату х, колеблются в одной фазе.

[3] Точность – величина обратная относительной погрешности измерения s, где s= (m_г -m_и) / m_г. В нашем примере s=10^–12.

[4] От латинского dissipatio – рассеяние. Диссипацию энергии понимают как переход энергии упорядоченного движения в энергию хаотического – теплового движения.

[5] Функции Y₁(x) и Y₂(x) называют линейно независимыми, если равенство Y = c₁Y₁+c₂Y₂ выполняется только при с₁ = с₂ = 0.

[6] Аэродинамика изучает законы движения воздуха и силы, возникающие на поверхности тел, относительно которых происходит его движение. В аэродинамике рассматривают движение со скоростями меньше, чем скорость звука в газе (скорость звука в воздухе равна 340 м/с, или 1200 км/ч).

Дата добавления: 2013-12-12