
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
При помощи структурных схем
|
|
|
|
Вопрос 26. Прогнозирование надежности машин
Вопрос 25. Этапы прогнозирования надежности машин.
Вопрос 24. Основные задачи прогнозирования надежности машин.
Вопрос 23. Определение доверительных границ показателей надежности
Вопрос 22. Критерии согласия. Проверка гипотезы о соответствии эмпирических и теоретических законов распределений
Вопрос 21. Построение графиков статистических функций распределения показателей надежности. Выбор закона распределения.
Вопрос 20. Анализ резко выделяющихся значений
Вопрос 19. Построение и группировка вариационного ряда.
Вопрос 18. Обработка статистической информации для оценки показателей надежности.
Вопрос 17. Экспоненциальный (показательный) закон распределения.
Вопрос 16. Закон распределения Вейбулла.
Вопрос 15. Нормальный закон распределения.
Нормальный закон распределения применяют при изучении постепенных отказов, износа, при исследовании процессов, на изменение которых влияет большое число факторов. К нормальному близки распределения значений наработки на отказ большинства изнашивающихся деталей машин. Часто нормальный закон распределения используют для определения суммарной наработки восстанавливаемых ремонтируемых изделий, наработки до отказа невосстанавливаемых изделий.

Вероятность безотказной работы изделия на интервале времени от 0 до t

Вероятность отказа изделия на интервале времени от 0 до t
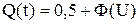
Частота отказов изделия или плотность вероятности времени безотказной работы изделия

Интенсивность отказов
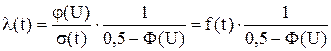
где 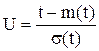 ,
,
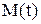 - среднее значение случайной величины;
- среднее значение случайной величины;
 - дисперсия случайной величины;
- дисперсия случайной величины;
 - функция Лапласа, обладающая следующими свойствами:
- функция Лапласа, обладающая следующими свойствами:
1. 
2. 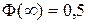
3.  - функция нечетная
- функция нечетная
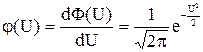 - производная функции Лапласа
- производная функции Лапласа
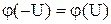 - функция четная
- функция четная
Значения функций и
и 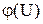 приведены в таблицах.
приведены в таблицах.
Разновидностями нормального распределения являются усеченное нормальное и логарифмическое нормальное распределения.
Усеченное нормальное распределение – распределение, пи котором из рассмотрения исключены значения случайных величин, лежащие вне интервала 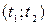 . Усечение может быть и односторонним.
. Усечение может быть и односторонним.
Усеченное нормальное распределение применяется при постепенных отказах изделий и их деталей, анализе надежности бурового оборудования.
Логарифмическое нормальное распределение – распределение, при котором логарифм случайной величины распределен по нормальному закону распределения. Такое распределение применяется при оценке результатов испытаний на усталостную прочность, расчете долговечностей деталей машин, эксплуатируемых в однородных условиях.
Закон распределения Вейбулла – один из самых распространенных в теории надежности. Этому закону следуют усталостная долговечность изделий, наработка до отказа невосстанавливаемых изделий. С помощью распределения Вейбулла можно описывать разнообразные причины отказов: усталостные, внезапные, постепенные. Закону распределения Вейбулла подчиняются отказы коробок скоростей, буровых лебедок, забойных двигателей, тракторов.

Вероятность безотказной работы изделия на интервале времени от 0 до t

Вероятность отказа изделия на интервале времени от 0 до t

Частота отказов изделия или плотность вероятности времени безотказной работы изделия

Интенсивность отказов
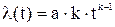
Среднее время безотказной работы
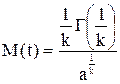
где a, k - параметры закона распределения Вейбулла;
Г(x) - гамма-функция, значения которой приведены в таблицах.
При k = 1 распределение Вейбулла переходит в экспоненциальное;
При k =2,5-3,5 – распределение Вейбулла близко к нормальному.
Экспоненциальный закон распределения является частным случаем закона распределения Вейбулла (k=1). Применим к изделиям, прошедшим предварительную приработку. Это распределение используется также при анализе внезапных отказов буровых насосов, горных машин.
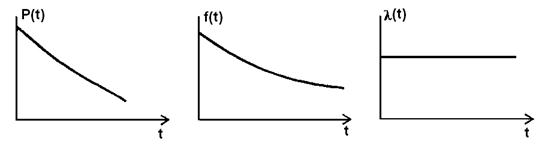
Вероятность безотказной работы изделия на интервале времени от 0 до t

Вероятность отказа изделия на интервале времени от 0 до t
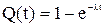
Дифференциальная функция или плотность вероятности экспоненциального распределения

Интенсивность отказов

Математическое ожидание при экспоненциальном распределении

Знание теоретических законов распределения показателей надежности нефтепромыслового оборудования дает возможность прогнозировать надежность техники на определенный период с определенной вероятностью и с учетом этого строить техническую политику в области эксплуатации (планировать ТО и Р, разрабатывать организационно-технические мероприятия, планировать запас запасных частей и т.д.).
Если закон распределения неизвестен, то для приближенного определения показателей надежности прибегают к методам математической статистики.
Обработка статистической информации о надежности ведется в следующей последовательности:
1. Построение вариационного ряда
2. Группировка вариационного ряда
3. Расчет параметров статистического распределения (математическое ожидание, среднее квадратичное отклонение, дисперсия, коэффициент вариации)
4. Оценка резко выделяющихся статистических данных (критерий Груббса)
5. Построение эмпирических кривых
6. Выбор теоретического закона распределения показателей надежности (нормальный, экспоненциальный законы, закон Вейбулла)
7. Проверка гипотезы о соответствии эмпирического закона распределения с помощью критериев согласия (критерии Пирсона, Романовского, Колмогорова)
8. Определение доверительных границ показателей надежности
Результаты наблюдений за надежностью машин и их элементов в том виде, как они получены по данным первичной учетной документации, представляют собой ряд неупорядоченных чисел, указывающих наработку изделий до отказов, ресурсы изделий и др.
Для построения статистического ряда полученные данные располагают в порядке увеличения значений наработки. В таком виде данные представляют собой вариационный ряд.
Затем показатели вариационного ряда группируют, т.е. подразделяют на К интервалов. Число интервалов К определяют в зависимости от объема выборки. Если число интервалов слишком большое, то картина распределения будет искажена отсутствием опытных точек в отдельных интервалах, а при малом числе интервалов будут сглажены характерные особенности распределения. На практике чаще всего число интервалов берут в пределах 7-14.
Для определения числа интервалов можно также применять формулу  .
.
Расчетную величину интервала определяют по формуле

где R – зона рассеивания, значение которой определяют по формуле:
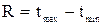
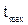 ,
, 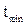 - соответственно максимальное и минимальное значения наработки.
- соответственно максимальное и минимальное значения наработки.
Полученное расчетное значение интервала  округляют до целого числа.
округляют до целого числа.
Определяют границы каждого интервала  , середину интервала
, середину интервала  , число отказов ni и частоту отказов
, число отказов ni и частоту отказов 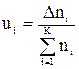 для каждого интервала.
для каждого интервала.
Данные представляют в виде таблицы:
| Номер интервала i | Интервал времени, 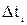 , ч , ч
| Середина интервала 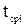 , ч , ч
| Число отказов 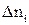
| Частота отказов 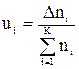
|
Часто при предварительном просмотре исходных данных возникают сомнения в истинности отдельных наблюдений, резко выделяющихся на общем фоне. Возникает вопрос, можно ли объяснить обнаруженные отклонения только случайными колебаниями выборки или дело в существенных искажениях стандартных условий сбора статистических данных.
Единственно абсолютно надежным способом решения вопроса резко выделяющихся наблюдений является тщательное рассмотрение условий, при которых эти наблюдения регистрировались. Однако во многих случаях это принципиально невозможно. Поэтому необходимо обращаться к соответствующим формальным статистическим методам.
Приближенно оценку информации на выпадающие точки проводят по правилу «Трех сигм»:  . Если значения случайной величины не выходят за пределы
. Если значения случайной величины не выходят за пределы  , все точки информации считаются действительными.
, все точки информации считаются действительными.
Для более точной проверки применяют специальные критерии: Груббса, Ирвина и Романовского.
1.Критерий Груббса (Приложение 6) вычисляют по формулам:
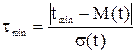 ,
,
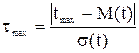 ,
,
где 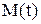 - математическое ожидание (расчетное);
- математическое ожидание (расчетное);
 - среднее квадратичное отклонение (расчетное).
- среднее квадратичное отклонение (расчетное).
Для заданного уровня значимости 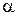 , значения которого могут составлять 0,01, 0,05, 0,1 и т.д., и количества наблюдаемых объектов N определяют критическое значение критерия Граббса (Приложение 6).
, значения которого могут составлять 0,01, 0,05, 0,1 и т.д., и количества наблюдаемых объектов N определяют критическое значение критерия Граббса (Приложение 6).
Если 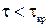 , то крайние члены не исключают из рассматриваемой совокупности. Если
, то крайние члены не исключают из рассматриваемой совокупности. Если  , то крайние члены исключают из рассматриваемой совокупности.
, то крайние члены исключают из рассматриваемой совокупности.
Пример 1. Проверим крайние точки статистической информации о наработке турбобура дор отказа по критерию Граббса:  ,
, 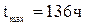 ,
, 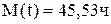 ,
,  ч, объем выборки N = 25, уровень значимости
ч, объем выборки N = 25, уровень значимости  .
.
 ,
,
 ,
,
Для заданного уровня значимости  и количества наблюдаемых объектов N = 25 по приложению 6 определяем критическое значение критерия Граббса
и количества наблюдаемых объектов N = 25 по приложению 6 определяем критическое значение критерия Граббса 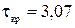 .
.
Т.к.  и
и  , то крайние члены не исключают из рассматриваемой совокупности.
, то крайние члены не исключают из рассматриваемой совокупности.
2. Критерий Романовского (приложение 4).
При применении критерия Романовского вычисляют математическое ожидание M(t) и среднее квадратичное отклонение  (t) без учета сомнительного члена ряда распределения t.
(t) без учета сомнительного члена ряда распределения t.
Если  при объеме выборки N, то с выбранной доверительной вероятностью
при объеме выборки N, то с выбранной доверительной вероятностью 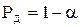 данный результат можно исключить из дальнейшего рассмотрения.
данный результат можно исключить из дальнейшего рассмотрения.
Доверительной считается такая вероятность, которую можно признать достаточной для суждения о достоверности характеристик, полученных на основе выборочных наблюдений. В качестве доверительной вероятности принимают значения 0,95; 0,99; 0,999 (последняя обеспечивает более надежные выводы). Для инженерных расчетов приемлемой является доверительная вероятность РД= 0,95.
3. Критерий Ирвина (приложение 5)..

где 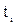 и
и  - смежные точки информации.
- смежные точки информации.
Расчет  ведется по всей статистической информации. Если значение
ведется по всей статистической информации. Если значение  при данном N, то анализируемая величина исключается из дальнейшего рассмотрения с вероятность 0,95 или 0,99.
при данном N, то анализируемая величина исключается из дальнейшего рассмотрения с вероятность 0,95 или 0,99.
По данным статистического ряда вычисляют эмпирические оценки показателей надежности оборудования.
Статистическую оценку вероятности безотказной работы оборудования определяют по формуле:
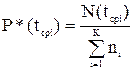 ,
,
где  - количество изделий, исправных к моменту времени
- количество изделий, исправных к моменту времени  ;
;
 - объем выборки.
- объем выборки.
Статистическую оценку вероятности отказа оборудования определяют по формуле:
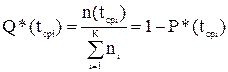 .
.
где  - количество изделий, отказавших к моменту времени
- количество изделий, отказавших к моменту времени 
Статистическую частоту отказов определяют по формуле:
 .
.
где 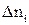 - количество изделий, отказавших за интервал времени
- количество изделий, отказавших за интервал времени 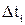 .
.
Статистическую интенсивность отказов определяем по формуле:
 .
.
Данные расчетов сводят в таблицу
| Номер интервала i | Интервал времени, ∆ti, ч | Середина интервала tсрi, ч | Число отказавших изделий ∆ni за время ∆ti | Число отказавших изделий n(tсрi) к моменту времени tсрi | N(tсрi)=N(0)-n(tсрi) | 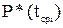
| 
| 
| 
|
По данным таблицы строят кривые распределения  ,
,  ,
,  ,
,  .
.
При построении графиков рекомендуется выбирать масштаб, пользуясь правилом «золотого сечения», т.е. график расположить в прямоугольнике, в котором высота относится к его ширине как 5 к 8.
По виду кривых выбирают закон распределения случайной величины: нормальный, экспоненциальный, Вейбулла.
Критерии согласия применяют для оценки близости экспериментальных (опытных) и теоретических распределений показателей надежности.
Критерии согласия позволяют ответить на вопрос: вызвано ли расхождение опытного и теоретического распределений случайными причинами, связанными с недостаточным числом наблюдений, или существенными причинами, т.е. тем, что теоретическое распределение плохо воспроизводит фактическое.
Критерий согласия выступает обычно в виде некоторой величины, оцениваемой с определенной вероятностью. Наиболее часто в качестве критериев согласия опытных и теоретических распределений показателей надежности принимаются критерии: Пирсона (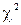 ), Романовского, Колмогорова
), Романовского, Колмогорова  .
.
Критерий Пирсона (хи - квадрат 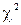 )
)
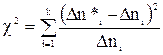
где  - эмпирические частоты случайной величины (отказов, например) в заданном временном интервале (определяется по результатам наблюдений);
- эмпирические частоты случайной величины (отказов, например) в заданном временном интервале (определяется по результатам наблюдений);
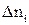 - теоретические частоты случайной величины в том же интервале (получается подставкой численных значений в формулу теоретического распределения, принятого для данного случая);
- теоретические частоты случайной величины в том же интервале (получается подставкой численных значений в формулу теоретического распределения, принятого для данного случая);
К - количество интервалов наблюдения.
Полученное значение 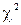 сравнивают с табличным значением
сравнивают с табличным значением  этого критерия.
этого критерия.
Величина  определяется по специальным математико-статистическим таблицам в зависимости от числа степеней свободы r и доверительной вероятности РД.
определяется по специальным математико-статистическим таблицам в зависимости от числа степеней свободы r и доверительной вероятности РД.
Число степеней свободы

где s - число параметров теоретического распределения (для нормального распределения и распределения Вейбуллаs=2; для экспоненциального s=1).
При выполнении условия 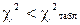 расхождения между теоретическими и эмпирическими частотами считают случайными, а теоретическое распределение показателей надежности - не противоречащим опытному.
расхождения между теоретическими и эмпирическими частотами считают случайными, а теоретическое распределение показателей надежности - не противоречащим опытному.
При  гипотезу отвергают.
гипотезу отвергают.
При использовании критерия 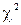 необходимо, чтобы объем вариационного ряда и число интервалов наблюдения были достаточно велики (что является определенным недостатком данного критерия). Количество отказов обследуемых машин, узлов, агрегатов должно превышать 50, а количество отказов в одном временном интервале должно быть больше 5. При выполнении этих условий критерий Пирсона является состоятельным, т.е. он почти всегда опровергает неверную гипотезу. Если же условия не выполняются, некоторые интервалы приходится объединять, что приводит к определенной погрешности.
необходимо, чтобы объем вариационного ряда и число интервалов наблюдения были достаточно велики (что является определенным недостатком данного критерия). Количество отказов обследуемых машин, узлов, агрегатов должно превышать 50, а количество отказов в одном временном интервале должно быть больше 5. При выполнении этих условий критерий Пирсона является состоятельным, т.е. он почти всегда опровергает неверную гипотезу. Если же условия не выполняются, некоторые интервалы приходится объединять, что приводит к определенной погрешности.
Для оценки приближения эмпирического распределения к теоретическому используется критерий согласия Романовского, который определяется по формуле:
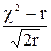
где 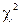 - критерий Пирсона;
- критерий Пирсона;
r - число степеней свободы.
Если выполняется условие 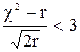 , то это дает основание для утверждения, о возможности принятия теоретического распределения показателей надежности за закон данного распределения.
, то это дает основание для утверждения, о возможности принятия теоретического распределения показателей надежности за закон данного распределения.
Критерий Колмогорова  позволяет оценить справедливость гипотезы о законе распределения при малых объемах наблюдений случайной величины
позволяет оценить справедливость гипотезы о законе распределения при малых объемах наблюдений случайной величины

где D - максимальная разность между фактической и теоретической накопленными частотами случайной величины.
На основе специальных таблиц определяют вероятность Р[ ] того, что если конкретный вариационный признак распределен по рассматриваемому теоретическому распределению, то из-за чисто случайных причин максимальное расхождение между фактическими и теоретическими накопленными частотами будет не меньшим, чем фактически наблюдаемое.
] того, что если конкретный вариационный признак распределен по рассматриваемому теоретическому распределению, то из-за чисто случайных причин максимальное расхождение между фактическими и теоретическими накопленными частотами будет не меньшим, чем фактически наблюдаемое.
На основе вычисленной величины Р[ ] делают выводы:
] делают выводы:
а) если вероятность Р[ ] достаточно велика, то гипотезу о том, что фактическое распределение близко к теоретическому, можно считать подтвержденной;
] достаточно велика, то гипотезу о том, что фактическое распределение близко к теоретическому, можно считать подтвержденной;
б) если же вероятность Р[ ] мала, то гипотеза отвергается.
] мала, то гипотеза отвергается.
Границы критической области для критерия Колмогорова зависят от объема выборки: чем меньше число результатов наблюдений, тем выше необходимо устанавливать критическое значение вероятности.
Если число отказов при наблюдении составило 10-15, то 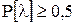 , если больше 100, то
, если больше 100, то 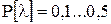 . Однако необходимо отметить, что при больших объемах наблюдений
. Однако необходимо отметить, что при больших объемах наблюдений  лучше пользоваться критерием Пирсона
лучше пользоваться критерием Пирсона 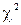 .
.
Критерий Колмогорова значительно проще других критериев согласия, поэтому он находит широкое применение в исследовании надежности машин и элементов.
Доверительные границы указывают, в каких пределах с заданной доверительной вероятностью может изменяться одиночный показатель надежности.
Рекомендуется применить значение доверительной вероятности  .
.
Доверительные границы рассеивания среднего значения при нормальном распределении равны:
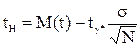 ,
,
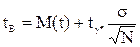 .
.
Значение  в зависимости от доверительной вероятности
в зависимости от доверительной вероятности  и числа степеней свободы
и числа степеней свободы  определяем по таблице ГОСТ 11.004-74.
определяем по таблице ГОСТ 11.004-74.
Доверительные границы рассеивания среднего значения при распределении Вейбулла равны:
 ,
,
 ,
,
где 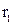 ,
, 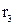 - коэффициенты, определяемые по таблицам 12, 13.
- коэффициенты, определяемые по таблицам 12, 13.
Для экспоненциального закона распределения расчет доверительных границ рассеивания ведем по формулам:
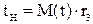 ,
,
 .
.
Для определения закономерностей изменения технического состояния машины в процессе работы выполняется прогнозирование надежности машин.
Различают три этапа прогнозирования: ретроспекцию, диагностику и прогноз. На первом этапе устанавливают динамику изменения параметров машины в прошлом, на втором этапе определяют техническое состояние элементов в настоящем, на третьем этапе прогнозируют изменение параметров состояния элементов в будущем.
Основные классы задач прогнозирования надежности машин могут быть сформулированы следующим образом:
1. Предсказание закономерности изменения надежности машин в связи с перспективами развития производства, внедрением новых материалов, повышением прочности деталей.
2. Оценка надежности проектируемой машины до того, как она будет изготовлена. Эта задача возникает на стадии проектирования.
3. Прогнозирование надежности конкретной машины (узла, агрегата) на основании результатов изменения ее параметров.
4. Прогнозирование надежности некоторой совокупности машин по результатам исследования ограниченного числа опытных образцов. С задачами такого типа приходится сталкиваться на этапе производства техники.
5. Прогнозирование надежности машин в необычных условиях эксплуатации (например, при температуре и влажности окружающей среды выше допустимой).
Специфика отрасли строительного машиностроения предполагает точность решения задач прогнозирования с погрешностью не более 10-15 % и использование методов прогнозирования, позволяющих получить решение задач в кратчайшие сроки.
Методы прогнозирования надежности машин выбирают с учетом задач прогнозирования, количества и качества исходной информации, характера реального процесса изменения показателя надежности (прогнозируемого параметра).
Современные методы прогнозирования могут быть разделены на три основные группы:
- методы экспертных оценок;
- методы моделирования, включающие физические, физико-математические и информационные модели;
- статистические методы.
Методы прогнозирования, основанные на экспертных оценках, заключаются в обобщении, статистической обработке и анализе мнений специалистов относительно перспектив развития данной области.
Методы моделирования базируются на основных положениях теории подобия. На основании подобия показателей модификации А, уровень надежности которой исследован ранее, и некоторых свойств модификации Б той же машины, прогнозируются показатели надежности Б на определенный период времени.
Статистические методы прогнозирования основаны на экстраполяции и интерполяции прогнозируемых параметров надежности, полученных в результате предварительных исследований. В основу метода положены закономерности изменения параметров надежности машин во времени.
При прогнозировании надежности машин придерживаются следующей последовательности:
1. Проводят классификация деталей и сборочных единиц по принципу ответственности. К деталям и сборочным единицам, отказы которых опасны для жизни людей, устанавливают более высокие требования безотказности.
2. Формулируют понятия отказа деталей и сборочных единиц проектируемой системы. При этом необходимо учитывать только те детали и сборочные единицы, отказ которых приводит к полной или частичной утрате работоспособности системы.
3. Выбирают метод прогнозирования надежности в зависимости от этапа проектирования системы, точности исходных данных и принятых допущений.
4. Составляют структурную схему изделия, включающую основные функциональные детали и сборочные единицы, в том числе детали и сборочные единицы силовых и кинематических цепей, расположенные по уровням в порядке их подчиненности, и отражающую связи между ними.
5. Рассматривают все детали и сборочные единицы, начиная с верхнего уровня структурной схемы и кончая нижним, с подразделением их на следующие группы:
а) детали и сборочные единицы, показатели которых следует определять расчетными методами;
б) детали и сборочные единицы с заданными показателями надежности, включая назначенные параметры потока отказов;
в) детали и сборочные единицы, показатели надежности которых следует определять опытно-статистическими методами или методами испытаний.
6. Для деталей и сборочных единиц, надежность которых определяют расчетными методами:
- определяют спектры нагрузок и другие особенности эксплуатации, для чего составляют функциональные модели изделия и его сборочных единиц, которые, например, могут быть представлены матрицей состояний;
- составляют модели физических процессов, приводящих к отказам,
- устанавливают критерии отказов и предельных состояний (разрушение от кратковременных перегрузок, наступление предельного износа и др).
- классифицируют их на группы по критериям отказов и выбирают для каждой группы соответствующие методы расчета.
7. Строят при необходимости графики зависимости показателей надежности от времени, на основании которых сравнивают надежности отдельных деталей и сборочных единиц, а также различных вариантов структурных схем системы.
8. Hа основании проведенного прогнозирования надежности делают вывод о пригодности системы для применения по назначению. Если расчетная надежность окажется ниже заданной, разрабатывают мероприятия, направленные на повышение надежности рассчитываемой системы.
При анализе надежности применяют метод структурных схем. Структурная схема представляет собой условную математическую и физическую модель изделия, по которой прогнозируется надежность в зависимости от уровня безотказности каждой детали и сборочной единицы.
Изделие при использовании структурных схем рассматривается как состоящее из отдельных элементов, предполагая, что отказ каждого элемента является независимым событием.
Различают последовательное, параллельное и комбинированное соединение элементов.

Под системой с последовательным соединением понимают такое соединение, когда отказ хотя бы одного элемента приведет к отказу всей системы.

Рисунок – Система с последовательным соединением элементов.
Вероятность безотказной работы системы n элементов в течение времени t определяют по формуле:

где Рi(t) - вероятность безотказной работы i-го элемента за время t.
Если элементы равнонадежные, то есть  , то вероятность безотказной работы системы:
, то вероятность безотказной работы системы:
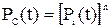 .
.
Вероятность отказа системы в течение времени t равна:

Частота отказов системы fc(t) определяется соотношением:
 .
.
Интенсивность отказов системы:
 ,
,
где  - интенсивность отказов i-го элемента;
- интенсивность отказов i-го элемента;
Среднее время безотказной работы системы:
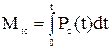 .
.
Система с параллельным соединение м элементов откажет лишь тогда, когда откажут все элементы.

Рисунок – Система с параллельным соединением элементов.
Вероятность безотказной работы системы при параллельном соединении n элементов в течение времени t будет равна:
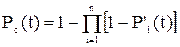 .
.
Если элементы равнонадежные, т.е.  , то
, то
 .
.
На практике одновременно встречаются оба вида соединения, тогда изделие рассматривается как смешанная система.

Рисунок – Система с комбинированным соединением элементов.
Вероятность безотказной работы в данном случае определяется по формуле:
 .
.
Надежность системы с последовательным соединением элементов с ростом даже высоконадежных элементов значительно уменьшается.
Повышение надежности системы достигается за счет параллельного соединения элементов, хотя конструктивно в механической системе этот способ не всегда может быть реализован, т.к. увеличивает габариты и массу нефтепромыслового оборудования.
|
|
|
|
Дата добавления: 2013-12-12; Просмотров: 578; Нарушение авторских прав?; Мы поможем в написании вашей работы!