Упорядоченная пара. Декартово произведение двух множеств

Глава 3. Соответствия

Контрольные вопросы

Понятие разбиения множества на классы

Число элементов объединения двух и трех конечных множеств

В математике часто приходится решать задачи, в которых требуется определить число элементов в множестве, либо в объединении или пересечении множеств.

Условимся число элементов конечного множества А обозначать п (А).

Пусть А = { a, b, c, d }, п (А) = 4; В = { e, f }, п (В) = 2. Множества А и В не пересекаются, т.е. А Ç В = Æ.

А È В ={ a, b, c, d, e, f }, п (А È В) = 6, т.е. п (А È В) = п (А) + п (В).

Рассмотрим еще один пример. А = { a, b, c, d }, п (А) = 4; В = { c, d, e }, п (В) = 3. В данном примере множества А и В пересекаются, т.е. А Ç В ¹ Æ.

А È В = { a, b, c, d, e }, п (А È В) = 5, т.е. п (А È В) ¹ п (А) + п (В).

Вообще, если заданы конечные множества, такие что А Ç В ¹ Æ, то число элементов в их объединении подсчитывают по формуле

п (А È В) = п (А) + п (В) – п (А Ç В).

Если даны три конечных множества А, В, С, то число элементов в их объединении можно найти по формуле:

п (А È В È С) = п (А) + п (В) + п (С) – п (А Ç В) – п (А Ç С) – п (В Ç С) + + п (А Ç В Ç С)

Понятие множества и операций над множествами позволяют уточнить наше представление о классификации.

Любая классификация связана с разбиением некоторого множества объектов на подмножества.

Определение. Множество А разбито на классы А ₁, А ₂,..., А_п, если:

1) подмножества А ₁, А ₂,..., А_п не пусты;

2) подмножества А ₁, А ₂,..., А_п попарно не пересекаются;

3) объединение подмножеств совпадает с множеством А.

Если не выполнено хотя бы одно свойство, то классификацию считают неправильной.

Например, если множество треугольников разбить на остроугольные, прямоугольные и тупоугольные, то разбиение будет выполнено верно, т.к. выполнены все условия, данные в определении.

Если из множества треугольников выделить подмножества равносторонних, равнобедренных и разносторонних треугольников, то разбиения мы не получим, т.к. множество равносторонних треугольников является подмножеством равнобедренных треугольников, т.е. не выполняется второе условие разбиения множества на классы.

Пример 1. Пусть А – множество двузначных чисел. Рассмотрим на этом множестве свойство «быть четным».

А

А ₂

А ₁

Множество А разбилось на два подмножества:

А ₁ – множество четных чисел,

А ₂ – множество нечетных чисел, при этом

А ₁ È А ₂ = А и А ₁ Ç А ₂ = Æ.

Т.о. задание одного свойства приводит к разбиению этого множества на 2 класса.

Пример 2. Пусть А – множество треугольников. Рассмотрим на данном множестве два свойства: «быть прямоугольным» и «быть равнобедренным». При помощи этих свойств из множества треугольников можно выделить 2 подмножества: В – множество прямоугольных треугольников и С – множество равнобедренных треугольников. Эти множества пересекаются, но ни одно из них не является подмножеством другого.

По рисунку видно, что получилось 4 класса:

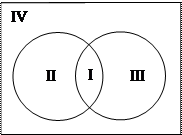I – В Ç С – множество равнобедренных прямоугольных треугольников;

II – В Ç 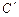– множество прямоугольных, но не равнобедренных треугольников;

III – 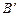Ç С – множество равнобедренных, но не прямоугольных треугольников;

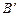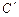IV – Ç – множество не равнобедренных и не прямоугольных треугольников.

Т.о. с помощью двух свойств множество разбилось на 4 класса, таких, что их пересечение пусто, а их объединение составляет множество А.

Следует отметить, что задание двух свойств приводит к разбиению множества на 4 класса не всегда.

Пример 3. Пусть А – множество треугольников. Рассмотрим на данном множестве два свойства: «быть прямоугольным» и «быть остроугольным». При помощи этих свойств из множества треугольников можно выделить 2 подмножества: В – множество прямоугольных треугольников и С – множество остроугольных треугольников. Эти множества не пересекаются. По рисунку видно, что при помощи этих свойств множество треугольников разбивается на три класса:

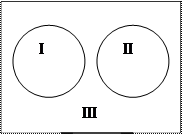I – множество прямоугольных треугольников;

II – множество остроугольных треугольников;

III – множество не прямоугольных, не остроугольных треугольников.

1. При каких условиях считают, что множество разбито на классы?

2. Как определить число элементов в объединении двух или трех конечных множеств?

Рассмотрим задачу: используя цифры 1, 2, 3, образуйте все возможные двузначные числа.

Запись каждого числа состоит из двух цифр, причем существенен порядок их следования (числа 12 и 21 различны).

В том случае, когда важен порядок следования элементов множества, в математике говорят об упорядоченных наборах элементах. В данном случае имеем дело с упорядоченной парой.

Упорядоченную пару, образованную из элементов а, b обозначают (а; b).

а – первая компонента пары, b – вторая компонента пары.

Определение. Пары (а; b) и (с; d) равны тогда и только тогда, когда а = с и b = d.

В школьном курсе математики мы встречались с упорядоченными парами при использовании прямоугольной системы координат, в которой каждая точка имеет координаты, представляющие собой пару чисел.

Задача. А = {1; 2}, В = {5; 6}. Составьте все возможные двузначные числа, число десятков которого принадлежит множеству А, а число единиц – множеству В.

Такими числами будут 15, 25, 16, 26.

В процессе решения этой задачи из двух данных множеств А и В образовано новое множество, элементами которого являются упорядоченные пары чисел (1; 5), (2; 5), (1; 6), (2; 6). Это новое множество называют декартовым произведением множеств А и В.

Определение. Декартовым произведением множеств А и В называется множество пар, первая компонента которых принадлежит множеству А, а вторая компонента принадлежит множеству В.

Записывают: А ´ В = {(а; b)½ а Î А, b Î В }

Пример. А = {1; 2}, В = {3; 4}. А ´ В = {(1; 3); (2; 3); (1; 4); (2; 4)}; В ´ А = {(3; 1); (3; 2); (4; 1); (4; 2)}. А ´ В ¹ В ´ А, следовательно, декартово умножение не обладает свойством коммутативности.

Аналогично рассуждая, можно показать, что для этой операции не выполняется свойство ассоциативности.

Декартово произведение множеств есть множество, поэтому, как и всякое множество, его можно задать перечислением и указанием характеристического свойства.

Элементы декартова произведения удобно записывать при помощи таблицы:

В А
	(1; 2)	(1; 4)
	(2; 3)	(2; 4)

Каждый элемент множества А ´ В записывается в клетке, стоящей на пересечении соответствующей строки и столбца. Т.о. множество клеток этой таблицы представляет собой декартово произведение множеств А ´ В.

Декартово произведение множеств можно задать также

  у  

А

1 2 х

В

графом и графиком

Дата добавления: 2013-12-12