Свойства отношений

Понятие отношения. Способы задания отношений

Глава 4. Отношения на множестве

Контрольные вопросы

1. Дайте определение числовой функции. Перечислите способы задания функций.

2. Какое множество называют областью определения и множеством значений функции?

3. Какое множество точек координатной плоскости называют графиком функции?

4. Дайте определения постоянной функции, прямой пропорциональности, обратной пропорциональности, линейной функции, квадратичной функции и укажите их свойства.

Мы выяснили, что между элементами двух различных множеств существуют различные соответствия. Но различные связи, отношения существуют и между элементами одного и того же множества.

Например, на множестве студентов первого курса можно рассмотреть отношения: «х старше у», «х и у – друзья», «х и у учатся в одной группе» и т.д.

В математике рассматриваются такие отношения как «х > у», «х кратно у», «прямая х параллельна прямой у» и т.д.

В математике чаще всего рассматриваются отношения между двумя объектами. Их называют бинарными.

Определение. Отношением между элементами множества Х или отношением на множестве Х называется всякое подмножество декартова произведения Х ´ Х.

Другими словами: бинарное отношение – это соответствие, заданное на одном и том же множестве Х.

Обозначают отношения прописными буквами латинского алфавита: Р, Q, R и т.д.

Поскольку отношение есть частный случай соответствия, то и способы задания отношений будут те же, что и для соответствий.

Рассмотрим отношение «меньше», заданное на множестве Х = {1; 2; 3; 4}. Отношение задано указанием характеристического свойства. Зададим его перечислением: R = {(1; 2); (1; 3); (1; 4); (2; 3); (2; 4); (3; 4)}. Также данное отношение можно задать

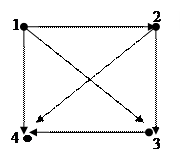таблицей

графом

графиком

Точки, изображающие элементы множества Х – вершины графа, стрелки – ребра графа.

Пример. Построим граф отношения «х кратно у», Х = {1; 2; 3; 4}.

Каждое число является делителем самого себя, поэтому для каждой точки множества рисуем стрелку, начало и конец которой совпадают (стрелку на графе, у которой начало и конец совпадают, называют петлей).

Графы отношений удобно использовать при решении логических задач, в том числе и в начальной школе.

Задача. Из лагеря вышли 5 туристов. Мы назовем их не в том порядке, в котором они идут один за другим: Вася, Аня, Толя, Лена и Миша. Толя идет впереди Миши, Лена – впереди Васи, но позади Миши, Аня – впереди Толи. Кто идет первым и кто идет последним? Кто идет вслед за Мишей, и кто идет перед Мишей?

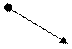
В задаче рассматривается два отношения: «идти впереди» и «идти позади». Выберем одно из них, например, «идти впереди», т.е. будем на графе ставить стрелку от впереди идущего к тому, кто идет вслед за ним. Граф будет выглядеть следующим образом:

Вася Аня

Толя

Миша

Лена

По графу можно легко ответить на все вопросы задачи: Первой идет Аня, последним – Вася, Вслед за Мишей идет Лена, а перед Мишей – Толя.

Отношение, заданное на множестве, может обладать рядом свойств, а именно:

1. Рефлексивность

Определение. Отношение R намножестве Х называется рефлексивным, если каждый элемент х множества Х находится в отношении R с самим собой.

Используя символы, это отношение можно записать в таком виде:

R рефлексивно на Х Û(" х Î Х) х R х

Пример. Отношение равенства на множестве отрезков рефлексивно, т.к. каждый отрезок равен себе самому.

Граф рефлексивного отношения во всех вершинах имеет петли.

2. Антирефлексивность

Определение. Отношение R намножестве Х называется антирефлексивным, если ни один элемент х множества Х не находится в отношении R с самим собой.

R антирефлексивно на Х Û(" х Î Х)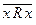

Пример. Отношение «прямая х перпендикулярна прямой у» на множестве прямых плоскости антирефлексивно, т.к. ни одна прямая плоскости не перпендикулярна самой себе.

Граф антирефлексивного отношения не содержит ни одной петли.

Заметим, что существуют отношения, не являющиеся ни рефлексивными, ни антирефлексивными. Например, рассмотрим отношение «точка х симметрична точке у» на множестве точек плоскости.

· у

l

х

Точка х симметрична точке х – истинно; точка у симметрична точке у – ложно, следовательно, мы не можем утверждать, что все точки плоскости симметричны сами себе, также мы не можем и утверждать, что ни одна точка плоскости не симметрична сама себе.

3. Симметричность

Определение. Отношение R намножестве Х называется симметричным, если из того, что элемент х находится в отношении R с элементом у, следует, что и элемент у находится в отношении R с элементом х.

R симметричнона Х Û(" х, у Î Х) х R у Þ у R х

Пример. Отношение «прямая х пересекает прямую у на множестве прямых плоскости» симметрично, т.к. если прямая х пересекает прямую у, то и прямая у обязательно будет пересекать прямую х.

Граф симметричного отношения вместе с каждой стрелкой из точки х в точку у должен содержать стрелку, соединяющую те же точки, но в обратном направлении.

4. Асимметричность

Определение. Отношение R намножестве Х называется асимметричным, если ни для каких элементов х, у из множества Х не может случиться, что элемент х находится в отношении R с элементом у и элемент у находится в отношении R с элементом х.

R асимметричнона Х Û(" х, у Î Х) х R у Þ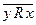

Пример. Отношение «х < у» асимметрично, т.к. ни для какой пары элементов х, у нельзя сказать, что одновременно х < у и у < х.

Граф асимметричного отношения не имеет петель и если две вершины графа соединены стрелкой, то эта стрелка только одна.

5. Антисимметричность

Определение. Отношение R намножестве Х называется антисимметричным, если из того что х находится в отношении с у, а у находится в отношении с х следует, что х = у.

R антисимметричнона Х Û(" х, у Î Х) х R у Ù у R х Þ х = у

Пример. Отношение «х £ у» антисимметрично, т.к. условия х £ у и у £ х одновременно выполняются только тогда, когда х = у.

Граф антисимметричного отношения имеет петли и если две вершины графа соединены стрелкой, то эта стрелка только одна.

6. Транзитивность

Определение. Отношение R намножестве Х называется транзитивным, если для любых элементов х, у, z из множества Х из того, что х находится в отношении с у, а у находится в отношении с z следует, что х находится в отношении с z.

R транзитивнона Х Û(" х, у, z Î Х) х R у Ù у R z Þ х R z

Пример. Отношение «х кратно у» транзитивно, т.к. если первое число кратно второму, а второе кратно третьему, то первое число будет кратно третьему.

Граф транзитивного отношения с каждой парой стрелок от х к у и от у к z содержит стрелку, идущую от х к z.

7. Связность

Определение. Отношение R намножестве Х называется связным, если для любых элементов х, у из множества Х х находится в отношении с у или у находится в отношении с х или х = у.

R связнона Х Û(" х, у, z Î Х) х R у Ú у R z Ú х = у

Другими словами: отношение R намножестве Х называется связным, если для любых различных элементов х, у из множества Х х находится в отношении с у или у находится в отношении с х или х = у.

Пример. Отношение «х < у» связно, т.к. какие бы мы действительные числа не взяли, обязательно одно из них будет больше другого или они равны.

На графе связного отношения все вершины соединены между собой стрелками.

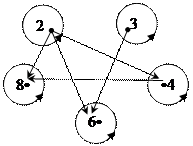Пример. Проверить, какими свойствами обладает

отношение «х – делитель у», заданное на множестве

Х = {2; 3; 4; 6; 8}.

Построим граф данного отношения:

1) данное отношение рефлексивно, т.к. каждое число из данного множества является делителем самого себя;

2) свойством антирефлексивности данное отношение не обладает;

3) свойство симметричности не выполняется, т.к. например, 2 является делителем числа 4, но 4 делителем числа 2 не является;

4) данное отношение антисимметрично: два числа могут быть одновременно делителями друг друга только в том случае, если эти числа равны;

5) отношение транзитивно, т.к. если одно число является делителем второго, а второе – делителем третьего, то первое число обязательно будет делителем третьего;

6) отношение свойством связности не обладает, т.к. например, числа 2 и 3 на графе стрелкой не соединены, т.к. два различных числа 2 и 3 делителями друг друга не являются.

Таким образом, данное отношение обладает свойствами рефлексивности, асимметричности и транзитивности.

Дата добавления: 2013-12-12