Высказывания с кванторами и их отрицания

Предикаты и операции над ними

Глава 5. Предикаты и теоремы

В математике часто встречаются предложения, содержащие одну или несколько переменных, например: «х + 2 = 7», «город стоит на Волге». Эти предложения не являются высказываниями, т.к. о них нельзя сказать, истинны они или ложны. Однако при подстановке конкретных значений переменной х они обращаются в истинные или ложные высказывания. Так, в первом примере при х = 5 получаем истинное высказывание, а при х = 3 – ложное высказывание.

Определение. Предложение с переменными, которое при конкретных значениях переменных обращается в высказывание, называется высказывательной формой или предикатом.

По числу входящих в предикат переменных различают одноместные, двухместные и т.д. предикаты и обозначают А (х), В (х;у)…

Пример: А (х): «х делится на 2» – одноместный предикат, В (х; у): «прямая х перпендикулярна прямой у» – двухместный предикат.

Следует иметь в виду, что в предикате переменные могут содержаться неявно: «число делится на 2», «студент получил отличную оценку на экзамене по математике».

Задание предиката, как правило, предполагает и задание множества, из которого выбираются значения переменных, входящих в предикат.

Определение. Множеством (областью) определения предиката называется множество Х, состоящее из всех значений переменных, при подстановке которых в предикат последний обращается в высказывание.

Так, предикат «х > 2» можно рассматривать на множестве натуральных чисел или действительных чисел.

Каждый предикат А (х), х Î Х определяет множество Т Ì Х, состоящее из элементов, при подстановке которых в предикат А (х) вместо х получается истинное высказывание.

Определение. Множество, состоящее из всех тех значений, при подстановке которых в предикат получается истинное высказывание, называется множеством истинности предиката (обозначается Т).

Пример. Рассмотрим предикат А (х): «х < 5», заданный на множестве натуральных чисел. Т = {1; 2; 3; 4}.

Предикаты, как и высказывания, бывают элементарными и составными. Составные предикаты образуются из элементарных при помощи логических связок.

Пусть Т_А – область истинности предиката А (х), Т_В – область истинности предиката В (х).

Определение. Конъюнкцией предикатов А (х) и В (х) называется предикат А (х) Ù В (х), который истинен для тех и только тех значениях х Î Х, для которых оба предиката истинны.

Покажем, что Т_{А Ù В} = Т_А Ç Т_В.

Доказательство. 1) Пусть а Î Т_{А Ù В} Þ А (а) Ù В (а) – истинное высказывание. По определению конъюнкции имеем: А (а) – истинно, В (а) – истинно Þ а Î Т_А Ù а Î Т_В Þ а Î Т_А Ç Т_В Þ Т_{А Ù В} Ì Т_А Ç Т_В.

2) Пусть b Î Т_А Ç Т_В Þ b Î Т_А Ù b Î Т_В Þ А (b) – истинно, В (b) – истинно Þ по определению конъюнкции А (b) Ù В (b) – истинное высказывание Þ b Î Т_{А Ù В} Þ Т_А Ç Т_В Ì Т_{А Ù В} .

Т.к. Т_{А Ù В} Ì Т_А Ç Т_В и Т_А Ç Т_В Ì Т_{А Ù В} , то по свойству равенства множеств Т_{А Ù В} = Т_А Ç Т_В, что и требовалось доказать.

Заметим, что полученное правило справедливо и для предикатов, содержащих более одной переменной.

Пример. Рассмотрим предикаты А (х): «х < 10», В (х): «х делится на 3», заданные на множестве натуральных чисел. Найдем область истинности предиката А (х) Ù В (х): «х < 10 и делится на 3».

Т_А = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10}, Т_В = {3; 6; 9; 12; 15; …}, тогда Т_{А Ù В} = {3; 6; 9}.

Определение. Дизъюнкцией предикатов А (х) и В (х) называется предикат А (х) Ú В (х), который истинен для тех и только тех значениях х Î Х, для которых истинен хотя бы один из предикатов.

Можно доказать (самостоятельно), что Т_{А Ú В} = Т_А È Т_В.

Пример. Рассмотрим предикаты А (х): «х делится на 2», В (х): «х делится на 3», заданные на множестве натуральных чисел. Найдем область истинности предиката А (х) Ú В (х): «х делится на 2 или на 3».

Т_А = {2; 4; 6; 8; 10;…}, Т_В = {3; 6; 9; 12; 15; …}, Т_{А Ú В} = {2; 3; 4; 6; 8; 9; …}.

Определение. Отрицанием предиката А (х)называется предикат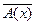. Он истинен для тех и только тех значениях х Î Х, для которых предикат А (х) ложен и наоборот.

Заметим, что = .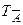

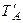Определение. Импликацией предикатов А (х) и В (х) называется предикат А (х) Þ В (х) (читают: «Если А (х), то В (х)»). Он обращается в ложное высказывание при тех значениях х Î Х, для которых предикат А (х) истинен, а предикат В (х) ложен.

Из определения имеем, что предикат А (х) Þ В (х) ложен на множестве Т_А Ç 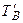, а следовательно истинен на дополнении к этому множеству. Воспользовавшись законами операций над множествами, имеем: .

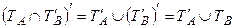Контрольные вопросы

1. Что называется высказывательной формой или предикатом?

2. Какие различают предикаты по числу входящих в них переменных? Приведите примеры.

3. Какое множество называют областью определения предиката?

4. Какое множество называют множеством истинности предиката?

5. Что называют конъюнкцией предикатов? Докажите равенство, связывающее область истинности конъюнкции предикатов с областями истинности этих предикатов.

6. Дайте определения дизъюнкции, отрицания, импликации предикатов. Запишите равенства, связывающие области истинности конъюнкции предикатов с областями истинности этих предикатов.

Если задан предикат, то, чтобы превратить его в высказывание, достаточно вместо каждой из переменных, входящих в предикат, подставить ее значение.

Например, если на множестве натуральных чисел задан предикат А (х): «х – четное число», то подставив вместо переменной число 4, получим истинное высказывание «4 – четное число», а, подставив вместо переменной число 5, получим ложное высказывание «5 – четное число».

Существуют и другие способы получения высказывания из предиката. Подставим перед этим предикатом слово «всякое», получим ложное предложение «Всякое натуральное число – четное». Если же перед предикатом подставим слово «некоторые», то получим истинное высказывание «Некоторые натуральные числа – четные».

Выражение «для всякого х» в логике называют квантором общности, обозначают " х.
В математике наряду со словом «всякий» употребляют слова «все», «каждый», «любой».

Высказывание (" х Î Х) А (х) выражает свойства всех объектов множества Х.

Выражение «для некоторых х» («существует х, такое, что …», «хотя бы один», «найдется») называют квантором существования и обозначают $ х.

Высказывание ($ х Î Х) А (х) выражает существование объектов из данного множества, обладающих определенными свойствами или находящимися в определенном отношении с другими объектами.

Таким образом, чтобы превратить предикат в высказывание, достаточно связать квантором общности или существования содержащиеся в нем переменные. Х.

Выясним, как установить значение истинности высказываний, содержащих кванторы.

Истинность высказываний с квантором общности устанавливается путем доказательства. Нужно убедиться в том, что при подстановке каждого из значений х в предикат последний обращается в истинное высказывание. Если множество Х конечно, то это можно сделать путем перебора всех случаев; если же Х бесконечно, то необходимо провести рассуждение в общем виде. Чтобы убедиться в ложности таких высказываний (опровергнуть их), достаточно привести контрпример.

Истинность высказывания с квантором существования устанавливается при помощи конкретного примера. Чтобы убедиться в ложности такого высказывания, необходимо провести доказательство.

Выясним, как построить отрицание высказываний, содержащих кванторы. Рассмотрим высказывание: «все натуральные числа – четные». Оно ложно. В этом легко убедиться, приведя контрпример: 5 не является четным числом. Можно перед данным предложением поставить слова «неверно, что». Тогда отрицанием высказывания: «все натуральные числа – четные» будет высказывание «неверно, что все натуральные числа – четные». Оно имеет тот же смысл, что и предложение «некоторые натуральные числа четными не являются».

Вообще если дано предложение (" х) А (х), то его отрицанием будут предложения 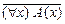и ($ х)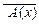, имеющие один и тот же смысл.

Рассмотрим высказывание «некоторые однозначные числа делятся на 10». Оно ложно. Отрицанием данного высказывания будет высказывание «неверно, что некоторые однозначные числа делятся на 10», которое имеет тот же смысл, что и высказывание «все однозначные числа делятся на 10».

Вообще если дано предложение ($ х) А (х), то его отрицанием будут предложения 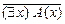и (" х)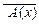, также имеющие один и тот же смысл.

Правило: для того чтобы построить отрицание высказывания с квантором общности (существования), достаточно заменить его квантором существования (общности) и построить отрицание предложения, стоящего после квантора.

Контрольные вопросы

1. Как можно предикат превратить в высказывание?

2. Приведите примеры слов, которые используются в качестве кванторов общности и существования.

3. Укажите способы установления значения истинности высказываний, содержащих кванторы?

4. Как построить отрицание высказываний, содержащих кванторы?

Дата добавления: 2013-12-12