Строение и виды теорем

Контрольные вопросы

1. Что значит предикат В (х) следует из предиката А (х)? В каком отношении находятся множества истинности этих предикатов?

2. В каком случае предикат А (х) будет являться необходимым условием для предиката В (х), достаточным условием для В (х)?

3. В каком случае предикаты А (х) и В (х) будут равносильны?

Теорема – это высказывание, истинность которого устанавливается посредством рассуждения (доказательства).

С логической точки зрения теорема представляет собой высказывание вида А Þ В, где А и В – предикаты с одной или несколькими переменными. Предложение А называют условием теоремы, а предложение В – ее заключением.

Рассмотрим теорему: «Если натуральное число делится на 2 и на 3, то оно делится на 6». Условие теоремы: «число делится на 2 и на 3», заключение теоремы: «число делится на 6». Условие и заключение теоремы представляют собой предикаты, заданные на множестве Х натуральных чисел. Данное предложение истинно при всех х из множества Х, следовательно, запись теоремы будет следующей: (" х Î Х) А (х) Þ В (х).

Т.о. в записи теоремы можно выделить 3 части:

1) разъяснительную (" х Î Х) – в ней описываются множества объектов, о которых идет речь в теореме;

2) условие теоремы: предикат А (х), заданный на множестве Х;

3) заключение теоремы: предикат В (х), заданный на множестве Х.

Для всякой теоремы вида (" х Î Х) А (х) Þ В (х) можно сформулировать предложения:

обратное данному (" х Î Х) В (х) Þ А (х),

противоположное данному (" х Î Х) ,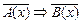

обратное противоположное данному (" х Î Х) .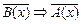

Заметим, что эти предложения не всегда является теоремами. Например, предложение, обратное для теоремы «если каждое слагаемое делится на данное число, то и сумма делится на данное число» будет ложным. Оно будет формулироваться так: «Если сумма делится на данное число, то и каждое слагаемое делится на данное число». Чтобы убедиться в том, что оно ложное, можно привести контрпример: 3 + 7 = 10. Сумма 10 делится на 5, но ни одно слагаемое на 5 не делится. Данные предложения будут теоремами только в том случае, если они истинны.

Пример. Рассмотрим предложение: «Если каждое слагаемое – четное число, то и сумма – четное число». В нашем примере предикат А (х): «каждое слагаемое – четное число», В (х): «сумма – четное число». Данное предложение является истинным, поэтому его можно назвать теоремой.

Построим обратное предложение: «Если сумма – четное число, то и каждое слагаемое – четное число». Оно ложное, т.к. можно привести контрпример 8 = 5 + 3.

Противоположное предложение: «Если хотя бы одно из слагаемых – нечетное число, то и сумма – нечетное число. Оно также ложно (можно воспользоваться тем же контрпримером).

Обратное противоположному предложение: «Если сумма – нечетное число, то хотя бы одно слагаемое – нечетное число». Оно истинно, поэтому оно также является теоремой.

Заметим, что прямое и обратное противоположному предложения всегда имеют одинаковые значения истинности, т.к. имеется равносильность (А Þ В) Û (В Þ А), называемая законом контрапозиции. Из этого предложения также следует, что предложения, обратное данному и противоположное данному также имеют одинаковые значения истинности. Поэтому, рассматривая их, достаточно доказать (или опровергнуть) какое-нибудь одно, тем самым будет доказано (или опровергнуто) другое.

Если для данное теоремы А (х) Þ В (х) существует обратная В (х) Þ А (х), то их можно соединить в одну А (х) Û В (х), в формулировке которой будут использоваться слова «необходимо и достаточно», «тогда и только тогда».

Заметим также, что если условие или заключение теоремы представляет собой конъюнкцию или дизъюнкцию, то, чтобы получить предложение, противоположное данному, нужно учитывать правила построения отрицания конъюнкции или дизъюнкции.

Дата добавления: 2013-12-12