Свойства сферического треугольника

Основные понятия сферической тригонометрии

Основы сферической астрономии

Литература к разделу

1. Кононович Э.В., Мороз В.И. Общий курс астрономии. Учебное пособие/Под ред. В.В. Иванова.- М.: Эдиториал УРСС, 2001-544с.

2. Куликовский П.Г. Справочник любителя астрономии. Изд. 5-е - М.:Эдиториал УРСС, 2002. -688с.

3. Ганагина И.Г. Астрономия. - Метод. указ. -Новосибирск: СГГА. - 2002.

4. Зигель Ф.Ю. Сокровища звёздного неба: Путеводитель по созвездиям и Луне. 5-е изд. М.: Наука, 1986- 296 с.

5. Михайлов А.А. Атлас звёздного неба [Электронный ресурс].- 4-е изд.- Л.: Наука, 1978, -17с.- Режим доступа: http://telescop.ucoz.ru/index/0-94. - Загл. с экрана.

На основании первого впечатления, в древности, люди представляли, что все светила расположены на вращающейся прозрачной сфере. Для установления – соотношения между дугами, соединяющих светила, углами, образующихся при пересечении дуг, потребовалось создать математический аппарат. Это послужило толчком для создания аппарата сферической тригонометрии.

Основные положения сферической тригонометрии. При всяком сечение сферы плоскостью Мы получаем окружность – круг. Если плоскость проходит через центр, то получается большой круг (БК) (рис.3.1).

Дуга БК является кратчайшим расстоянием на сфере между двумя точками (на плоскости прямая). В сферической тригонометрии рассматриваются только соотношения между дугами БК.

Прямая АА1, проходящая через центр плоскости БК, называется - геометрической осью БК, 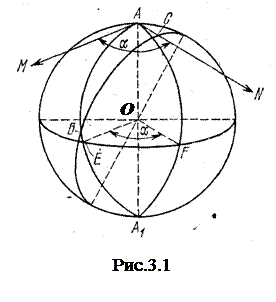точки А и А1 – сферические центы БК – полюса. Сам БК по отношению к полюсам называют полярой или экватором. Величина дуг от точек АА1 до экватора (сферическое расстояние) равно 90°.

АКСИОМА ¾ через две точки на сфере, не лежащие на одном диаметре, можно провести большой круг и при том только один.

Дуги больших кругов при пересечение образуют углы, которые называются сферическими.

Рассмотрим сферический угол FAE где FА и EA – стороны. FА=EA = 90 градусов; FE – дуга поляры (Экватора).

Сферический угол измеряется углом между касательными в точке А, т.е. угол NAM = сф. углу FAE. Из построения угол NAM = углу FOE =дуге FE. Т.е мерой сферического угла является дуга поляры, кроме того мерой сферического угла является и соответствующий ему двугранный угол. Кроме того, (без доказательства):

1. Вертикальный сферический угол равен 90°;

2. Сумма смежных сферических углов ровна 180°;

Для решения многих астрономических задач, таких, в частности, как переход от одной системы астрономических координат к другой, определение времени и азимута восхода и захода светил и т.п. рассматривается сферический треугольник и применяются его основные формулы. Сферический треугольник- фигура на сфере, образованная дугами трех больших кругов (рис. 3.1).

В сферической тригонометрии рассматриваются только треугольники со сторонами меньше 180° (эйлеровы треугольники). Углы в сферическом треугольнике, обозначают заглавными буквами, латинским алфавита (А, В, С), а противолежащие им стороны соответствующими малыми буквами (а, b, с).

По углам треугольники могут быть: косоугольные, прямоугольные.

По сторонам: разносторонние, равносторонние, равнобедренные, прямосторонние.

Если в сферическом треугольнике один угол равен 90°, треугольник называется прямоугольным. Сторона, лежащая против прямого угла ¾ гипотенуза, две другие ¾ катеты. Если треугольнике все углы равны 90°, то такой треугольник называется трижды прямоугольным. В этом случае стороны одновременно и гипотенузы, и катеты.

Если в сферическом треугольнике одна сторона равна 90°, треугольник называется прямосторонним. Сферические треугольники могут быть трижды прямосторонними.

Углы и стороны сферического треугольника измеряются в угловой мере!

На рис. 3.2 изображен косоугольный сферический треугольник ∆АВС. Углы треугольника: сф.ÐВАС=А; сф.ÐАВС=В; сф.ÐАСВ=С. Стороны сферического треугольника (мера угловая): дуга ВС=а; дуга АС=в; дуга АВ=с.

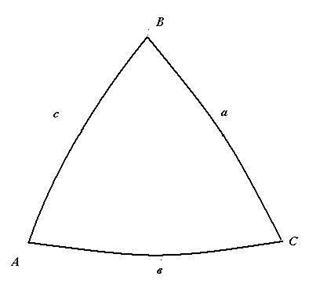
Рис. 3.2

Сферические треугольники обладают рядом свойств:

1. Любая сторона сф. треугольника меньше суммы и больше разности двух других сторон, т.е.:

а + b > c; b+ c > a; с + a > b;

b> a – c; a > b – c; c> b – a;

2. Сумма сторон cф. треугольника больше нуля и меньше 360°, т.е.: 0°<a+b+c<360°;

3. Сумма углов cф. треугольника больше 180° и меньше 540°, т.е.:

180°< A + B + C < 540°, величина e= A + B + C – 180° – называется сферическ4им избытком (эксцессом);

4. Сумма двух углов без третьего должна быть меньше 180° градусов

A + B – C <180°;

5. Если сумма двух углов сферического треугольника больше, равна или меньше 180°, то и сумма двух противоположным им сторон больше, равна или меньше 180°;

6. Если разность двух сторон сферического треугольника больше, равна или меньше нуля, то разность противолежащих им углов соответственно больше, равна или меньше нуля, т.е., если a – b > 0, то и A – B >0 и т.д..

Для прямоугольных сферических треугольников должна выполняться ещё два условия:

7. Число сторон, больше 90° – должно быть чётное, а меньше 90° – не чётное;

8. Катет и противолежащий ему угол, всегда лежат в одной четверти.

Дата добавления: 2013-12-12