Время на меридиане Гринвича

Связь среднего солнечного и звездного времени.

Из наблюдений известно, что в тропическом году содержится 365,2422 средних солнечных суток, и 366,2422 звёздных суток, а средние солнечные сутки содержат 24^h03^m59.6^s ср. звёздного времени, одни звёздные сутки содержат 23^h56^m04.09^s ср. солнечного времени . Причина различия можно понять из рисунка 3.20:

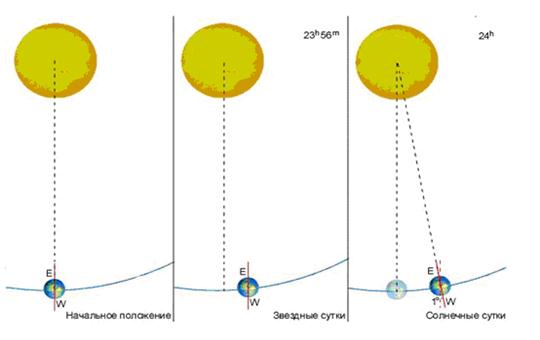
Рис. 3.20 Отличие звёздного и солнечного времени

Для вывода математической зависимости между шкалами звёздного и среднего солнечного времени запишем равенство:

365,2422 ср. солн. сут.= 366,2422 ср.зв. сут.,

поделив обе части на 365.2422 получим:

1 = 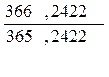=1,00273791, или

366,2422 ср.зв. единиц. =365,2422 ср. солн. единиц.´1,00273791.

Т.е., чтобы перевести промежуток времени, выраженный в средних солнечных единицах в звёздные его необходимо умножить на коэффициент 1,00273791.

Принято обозначать:

1,00273791=1+m, где m=0,00273791.

Можно записать:

Ds=Dm´(1+m).

Обратный переход (от звёздных единиц к солнечным) получим поделив обе части равенства (366,2422=365,2422) на 366,2422:

1 = 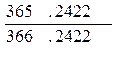= 0,99726957, или

365,2422 средних солнечных единиц =366,2422 средних звёздных единиц.´ 0,99726957,

т.е., чтобы перевести промежуток времени, выраженный в звёздных единицах в солнечные его необходимо умножить на коэффициент 0,99726957.

Принято обозначать:

0,99726957=1-n, где n=0,00273043.

Можно записать:

Dm=Ds´(1-n).

Время на меридиане Гринвича обозначают соответствующей большой

буквой S или M. Среднее солнечное время (M) на гринвичском меридиане еще называют всемирным (мировым) временем. Принятое международное обозначение всемирного времени - UT (Universal Time).

Звездное время в Гринвичскую полночь обозначают S₀. Оно дается в астрономических таблицах (А.Е.), на каждую дату года. Знание значения звёздного времени в определённые моменты всемирного, которое относится к системе солнечного времени, позволяет осуществлять переход между шкалами времени. Звёздное время связывает прямое восхождение светила и часовой угол

s=a+t,

поэтому для Солнца в нижней кульминации можно записать:

s=a_¤+12^h,

при этом для Гринвича это будет S_, но в течении суток a_¤ меняется мало, следовательно S₀».a_¤+12^h. Так как в моменты равноденствий и солнцестояний значения a_¤ известны, то можно приблизительно знать и значения S₀ для этих дат. В таблице 4 приведены значения прямого восхождения Солнца и звёздного времени для этих моментов.

Таблица4. Значения a_¤ и S₀ для равноденствий и солнцестояний

№ п/п	Астрономическое событие	Дата	a¤	S0
	Весеннее равноденствие	21.03	0^h00^m	12^h00^m
	Летнее солнцестояние	22.06	6^h00^m	18^h00^m
	Осеннее равноденствие	23.09	12^h00^m	0^h00^m
	Зимнее солнцестояние	22.12	18^h00^m	6^h00^m

В XIX веке было доказано, что земная ось и, следовательно, полюса Земли и меридиан Гринвича движутся. Поэтому различают всемирное время на мгновенном Гринвичском меридиане UT0 и UT1 ¾ всемирное время среднего Гринвичского меридиана. UT1 получается исправлением всемирного времени UT0 поправкой Dl за движение географических полюсов

UT1 = UT0+ Dl.

Поправка Dl зависит от координат мгновенного полюса x_p, y_p, отсчитываемых относительно общепринятого Международного условного начала (Conventional International Origin), и имеет вид

Dl=-(x_p×sinl y_p ×cosl)tanj,

где l, j ¾ координаты места наблюдения.

Дата добавления: 2013-12-12