Теория способа наименьших квадратов

Рис. 3. Несвободная сеть полигонов

Рис. 4. Сеть треугольников (центральная система)

Рис. 5. Геодезическое построение планового обоснования

а) цепочка треугольников; б) геодезический четырехугольник

С клавиатуры вводят либо координаты смежной точки, либо дирекционный угол (α_АВ) этого известного направления. Включают режим ориентирования теодолита и устанавливают режим работы теодолита – прямая задача.В случае необходимости съемки с точки А (точка А является станцией) рабочий с отражателем направляется на съемочную точку № 1 (пикет – точка контура или рельефа). На отражатель наводят теодолит и включают режим измерений. На индикаторе высветятся координаты X₁, Y₁, и высота H₁, которые вычисляются по формулам программного обеспечения теодолита. Эти формулы имеют следующий вид:

d₁ = D₁ Cos ν₁; (7)

α_А1 = α_АB + β_{Л 1} – 180°; (8)

X₁ = X_A + d₁ * Cos α_А1; (9)

Y₁ = Y_A + d₁ * Sin α_А1; (10)

H₁ = H_A + D₁*Sin ν₁ + i_А - l_А, (11)

где D₁ – расстояние от теодолита до отражателя, измеренное лазерным дальномером на точку 1; ν₁ – угол наклона, измеренный при визировании на точку 1;

β_{Л 1} – горизонтальный угол, измеренный от направления ориентирования теодолита до направления при визировании на точку 1 по направлению хода часовой стрелки.

Эти координаты записывают в память флеш-карты и действия повторяют для всех съемочных точек.

Если съемка с точки А закончена, то намечают переходную точку теодолитного хода. (Применяют сквозную нумерацию съемочных пикетов и переходных точек). На эту точку устанавливают отражатель и выполняют действия режима работы – прямая задача. Координаты и отметку переходной точки записывают в журнал измерений. Снимают теодолит и переносят его на переходную точку. Эта точка становиться станцией, на которой выполняют действия по установке теодолита в рабочее положение и ориентированию его на предыдущую станцию. Далее выполняют съемку по методике описанной выше. Такие действия выполняют на всех станциях.

При завершении съемочных работ теодолитный ход, состоящий из переходных точек (станций), должен быть закончен на точке (пункте), координаты и высота которой известны. Например, на пункте полигонометрии или триангуляции с координатами X_С', Y_C' и высотой H_C'. В этом случае измерениями с предыдущей станции получают координаты и высоту этой точки, X_С, Y_C, H_C. Завершают измерения на пункте С измерением угла β_Л при ориентировании теодолита на предыдущую станцию и на пункт D с известным дирекционным углом α_CD'. По формуле (8) вычисляют дирекционный угол α_CD. Запускают режим уравнивания измеренных углов, координат и высот станций. При этом программное обеспечение теодолита работает по следующим формулам:

f _β = α_CD - α_CD', если 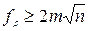, см. формулу (3), то на индикаторе высвечивается запись “недопустимая угловая невязка f _β =? ”;

если 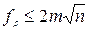, то β _i = β _i +(- f _β/ n), α_i+1 = α_i + β_i – 180°;

f _x = X_С - X_С', f _y = Y_С - Y_C', ;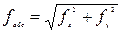

если f _абс/∑ d ≥ 0.0005, то на индикаторе высвечивается запись “недопустимая линейная невязка f _x =?; f _y =? ”;если f _абс/∑d ≤ 0.0005, то

X_i+1 = X_i + d_i * Cos α _i + 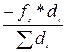; Y_i+1 = X_i + d_i * Sin α_i +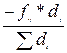

f _H = H_C - H_C'; если f _H ≥ 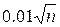, то на индикаторе высвечивается запись “недопустимая высотная невязка f _H = ”;

если f _H ≤ 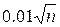, то H_i+1 = H_i + D_i*Sin ν_i + i_i – l_i + .

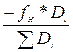После уравнивания координат и высот точек теодолитного хода автоматически пересчитываются координаты и высоты пикетных точек. Каталог координат и высот точек представляет собой цифровую модель местности.

Преобразование цифровой в аналитическую модель местности осуществляется на компьютере по специальной программе, например CREDO. Аналитическая модель дорабатывается до получения компьютерной версии плана местности. Для этого используются полевые записи о характеристике пикетных точек: точка контура, точка рельефа. Рисовка контурной части плана осуществляется в соответствии с условными знаками. Рисовку рельефа местности выполняют, используя специальные компьютерные программы, которые работают в аппрокимационном или интерполяционном режиме.

Съемка в режиме решения обратной геодезической засечки электронным теодолитом с запоминающим устройством в виде флеш-карты может иметь, как самостоятельный характер, так и при досьемке тех участков местности, которые по каким либо причинам были пропущены. При этом осуществляется следующая последовательность действий. Теодолит в рабочее положение устанавливается в произвольной точке, с которой удобно выполнять съемку местности или пропущенный участок. При этом необходимо чтобы была прямая видимость не менее чем на три точки, координаты которых известны. Дальнейший порядок работы аналогичен, тому который используется при определении координат методом обратной засечки и съемке местности в режиме решения прямой геодезической задачи.

1.3.2. Спутниковые методы геодезических измерений

Общие положения. В настоящее время имеют место две спутниковые системы определения координат точек земной поверхности. Это Российская система ГЛОНАС (ГЛОбальная НАвигационная Спутниковая Система) и американская система NAVSTAR GPS. С учетом обеспечения специальных поправок в спутниковые измерения точность определения приращений координат составляет не более 5 мм. При этом точность определения координат одиночного приемника составляет 10 – 100 м. То есть с очень высокой точностью устанавливаются относительные координаты и расстояния между точками и грубо устанавливаются сами значения координат.

Спутниковые системы состоят из трех сегментов: космического, контроля и управления и сегмента пользователя (приемник сигналов). Космический сегмент состоит из 21-о действующего и 3-х запасных спутников. Высота их над Землей и орбиты движения рассчитаны таким образом, что с каждой точки поверхности Земли видно не менее 4-х спутников. Сегмент контроля и управления состоит из взаимосвязанных стационарных элементов: центра управления, контрольных станций, командных станций слежения, квантово-оптических станций, которые обеспечивают работу бортовых систем спутников. Станции слежения принимают все сигналы проходящих над ними всех спутников, вычисляют расстояния до спутников, измеряют местные метеорологические параметры и передают информацию на главную станцию контроля. Приемники сигналов пользователя, которые используют геодезисты, принимают эти сигналы и путем специальных вычислений с учетом обработки информации получают криволинейные координаты (геодезические широту и долготу).

Следует отметить, что для исключения несанкционированного использования системы NAVSTAR GPS в эфемериды спутников умышленно вносятся искажения. Для исключения этих искажений используется специальный P-код. В этом случае точность определения координат точек Земли составляет 10 – 20 м. Обычный GPS-приемник, работающий без доступа к P-коду, может установить координаты точки с предельной погрешностью 150 – 200 м. В системе ГЛОНАС искажения не допускаются (С/А код), поэтому любой пользователь может установить координаты точки с предельной погрешностью 20 м.

В геодезии применяются приемники:

С/А код + фазовые измерения на частоте L₁;

С/А код + фазовые измерения на частоте L₁ и L₂;

В отдельных случаях при доступе P-коду приемник может работать в системе:

С/А код + P-код + фазовые измерения на частоте L₁ и L₂.

Рис. 6. Структурная схема приемника

1. Антенна и предусилитель; 2. Идинтификатор сигналов и распределение частот по каналам; 3. Микропроцессор для управления работой приемника; 4. Расшифровка принятой информации, вычисление абсолютных координат и поправок в часы приемника, выполнение фазовых измерений; 5. Кварцевый генератор; 6. Дисплей и панель управления; 7. Блок памяти для записи, накопления и хранения информации; 8. Блок питания.

Способ спутниковых измерений сводится к определению расстояния (псевдодальности) от спутника до точки, на которой установлен приемник. Псевдодальность D' устанавливают по формуле

D' = (T_П – Т_С) v, (12)

где T_П – момент приема сигнала на Земле; Т_С - момент излучения сигнала спутником;

v – скорость распространения электромагнитных волн.

Расстояние между спутником и приемником на момент измерений устанавливают по формуле

D + δtv = (T_П – Т_С) v,

или 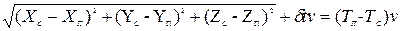, (13)

где X_C, Y_C, Z_C – координаты спутника на момент измерений; X_П, Y_П, Z_П – координаты приемника на момент измерений; δt – поправка на точность хода часов спутника и приемника.

В уравнении (13) неизвестными являются координаты приемника. Координаты спутника на момент измерения устанавливают по известной траектории движения этого спутника по орбите. Для определения неизвестных необходимо иметь, как минимум, четыре уравнения. Эти уравнения получают при одновременных измерениях на четыре спутника. Решением системы четырех уравнений получают искомые значения координат приемника. При этом используют метод наименьших квадратов.

Режим наблюдений. Как уже отмечалось абсолютная и относительная точность измерений координат точек Земной поверхности при использовании спутниковых измерений различается на порядок. Поэтому в практике геодезических измерений чаще используют относительные измерения как наиболее точные. Существуют несколько режимов относительных измерений, которые, в свою очередь подразделяются на две группы: статические и кинематические. При этом всегда один из приемников устанавливают на пункт с известными координатами, а другие - на определяемых точках.

Статический режим измерений как наиболее точный является основным при привязке трассы дороги к пунктам государственной сети. Однако требует достаточно больших затрат времени. Измерение относительных координат одного пункта составляет от 40 минут до нескольких часов. Продолжительность измерений зависит от необходимой точности получения относительных координат точек, числа и расположения в пространстве наблюдаемых спутников, состояния ионосферы Земли и др.

Режим быстрой статики, при котором время наблюдений сокращается до 10 – 15 минут. Информацию о завершении измерений получают от приемника при достаточном количестве информации. Для исключения больших (грубых) погрешностей из результатов измерений практикуют перестановку GPS-приемников, которые устанавливают на пунктах с известными координатами и на определяемые пункты.

Режим кинематики предполагает выполнение измерений на стационарном пункте с известными координатами и передвижным (роверным, англ. rover - скиталец) GPS-приемником. Для инициализации приемники устанавливают на расстоянии 2 – 3-х метров друг от друга и выполняют измерения в течение 15 – 20 минут. Затем с роверным приемником, переключенным в режим кинематики, перемещаются поочередно на определяемые пункты. Время измерений на этих пунктах 15 – 20 минут. Во время движения от одного пункта к другому GPS-приемник должен быть включен и отслеживать те же спутники, которые фиксируются GPS-приемником на стационарной точке. Завершение наблюдений роверным приемником осуществляют на точке инициализации.

Кинематика “в полете” – режим измерений при исключении события инициализации приемников. Этот режим применяется в том случае, если есть уверенность в том, что имеет место непрерывный (в течение 20 минут) и устойчивый прием сигнала не менее чем с четырех спутников.

Преобразование координат. При спутниковых измерениях появляется необходимость пересчета полученных координат (GPS – в системе WGS-84, ГЛОНАС – в ПЗ-90) в прямоугольные координаты систем СК-42 или СК-65. В этом случае необходимо знать параметры преобразования, к которым относятся: координаты смещения начал систем координат, углы разворота осей координат и масштабный коэффициент.

1.4. Теоретические основы уравнивания геодезических измерений

При создании съемочного обоснования может быть выполнено достаточное и избыточное количество измеренных элементов в геодезических построениях. При недостаточном количестве измерений нет возможности проконтролировать их правильность. Но при выполнении избыточных измерений увеличивается количество затраченного времени и уменьшается производительность труда. Поэтому после рекогносцировки, при составлении схемы (проекта) планово-высотного обоснования, необходимо планировать выполнение избыточных измерений. При этом следует стремиться к такой схеме измерений, при которой было бы минимальное количество избыточных измерений, но достаточное их количество для осуществления контроля правильности этих измерений (рис. 6). Например, для вычисления всех элементов треугольника достаточно измерить одну его сторону и два примыкающих к этой стороне угла (рис. 6а). Но проконтролировать правильность полученных результатов после вычисления всех элементов треугольника невозможно. Тогда как, выполнив избыточное измерение только одного третьего угла треугольника (см. рис. 6б) и сопоставив сумму этих углов со значением теоретической суммы равной 180°, появляется уверенность в правильности этих измерений. При этом нет необходимости выполнять большое количество избыточных измерений. Это не только уменьшает производительность труда, но и определяет лишние (чрезмерно избыточные) условия, которые порой трудно учесть при определении поправок в измеренные значения. Например, нет необходимости измерять все три угла и все три стороны в треугольнике. Выявленную погрешность измерений (невязку) можно распределить в измеренные параметры (вычислить поправки и уравнять), тем самым увеличить достоверность конечных результатов.

а) б)

Рис. 6. Достаточное (а) и избыточное (б) количество измерений в треугольнике для вычисления его элементов.

Кроме того, абсолютное значение погрешности (невязки) сопоставляется с допускаемой погрешностью. Допустимые или ожидаемые погрешности зависят от выбранного метода измерений и точности используемых приборов. Поэтому при проектировании сети планово-высотного обоснования следует помнить, что количество измерений должно быть необходимым и достаточным для определения правильности выполненных измерений и реализации математического метода определения поправок в измеренные параметры, а метод измерений и применяемые приборы соответствовать необходимой точности измерений.

Как известно, погрешности измерений бывают грубые, систематические и случайные. Грубые промахи в измерениях и систематические погрешности выявляются и исключаются из результатов измерений путем или повторных измерений (грубые промахи) или специальными методами (поправка за компарирование мерного прибора и др.). Грубые и систематические погрешности в данном случае нами не рассматриваются.

Случайные погрешности могут быть исключены из результатов измерений только путем уравнивания геодезических измерений. Процесс сопоставления функций измеренных параметров с их теоретическими значениями, вычисление случайных погрешностей (невязок), сравнение их с допустимыми и отбраковка недоброкачественных измерений, а также определение поправок в измеренные параметры по условию вычисления их вероятнейших значений, называется уравниванием геодезических измерений.

Для уравнивания используются методы математической обработки геодезических измерений. Необходимость уравнивания диктуется условием, при невыполнении которого может происходить одностороннее накопление погрешностей в конечных результатах измерений (координатах и отметках точек). Эти погрешности, в конечном итоге, могут превысить необходимую точность составляемого плана или точность определения точек проектируемого объекта на местности.

В зависимости от класса точности измерений при реализации математических методов различают:

· строгое уравнивание, когда вычисление поправок в измеренные параметры определяют путем составления и решения систем математических уравнений;

· нестрогое уравнивание, когда поправки в измеренные параметры вычисляют путем приближенного определения их вероятнейших значений.

Суть строгого и не строгого уравнивания поясним на примере уравнивания углов геодезического четырехугольника (рис. 7).

Пусть в этой сети измерены восемь углов β₁, β₂, β₃, β₄, β₅, β₆ β₇, β₈. Каждый угол измерен одним и тем же теодолитом с неизвестными погрешностями δβ₁, δβ₂, δβ₃, δβ₄, δβ₅, δβ₆ δβ₇, δβ₈. Для уравнивания необходимо в каждый угол ввести поправки v₁, v₂, v₃, v₄, v₅, v₆, v₇, v₈, которые с наибольшей вероятностью должны быть равны абсолютной величине погрешностей измерений и противоположны им по знаку.

Для строгого уравнивания геодезического четырехугольника составляют восемь уравнений с неизвестными поправками v₁, v₂, v₃, v₄, v₅, v₆, v₇, v₈

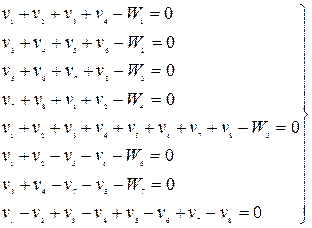(14)

где W₁, W₂, W₃, W₄, W₅ – невязки соответственно в треугольниках и четырехугольнике.

W₆, W₇ – невязки по суммам углов в смежных треугольниках.

Первые пять уравнений системы (14) определяются из следующих геометрических условий.

W₁ = β₁ + β₂ + β₃ + β₄ -180°;

W₂ = β₃ + β₄ + β₅ + β₆ - 180°;

W₃ = β₅ + β₆ + β₇ + β₈ - 180°; (15)

W₄ = β₇ + β₈ + β₁ + β₂ - 180°;

W₅ = β₁ + β₂ + β₃ + β₄ + β₅ + β₆ + β₇ + β₈ − 360°.

Следующие два уравнения в системе (14) определяются из условий

W₆= β₁ + β₂ – β₅ – β₆

W₇= β₃ + β₄ – β₇ – β₈

Последнее уравнение в системе (14) получено из условия

β₉ + β₁₀ + β₁₁ + β₁₂ = 360

где β₉ = 180° – (β₁ + β₂), так как v₉ = 0, то v₁ – v₂ = 0

β₁₀ = 180° – (β₃ + β₄), так как v₁₀ = 0, то v₃ – v₄ = 0

β₁₁ = 180° – (β₅ + β₆), так как v₁₁ = 0, то v₅ – v₆ = 0

β₁₂ = 180° – (β₇ + β₈), так как v₁₂ = 0, то v₇ – v₈ = 0

Математически строгое решение системы уравнений (14) приводит к искомому результату.

При не строгом уравнивании поправки определяются по тем же принципам, что и при строгом уравнивании. То есть, численные значения поправок равны их вероятнейшему значению из условия равноточности или неравноточности измеренных параметров. В любом случае удовлетворяются основные геометрические условия (15), по которым устанавливаются невязки.

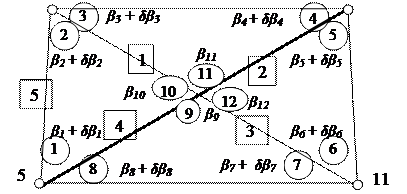Рис. 7. Схема опорной сети (геодезический четырехугольник)

В качестве основного теоретически обоснованного способа уравнивания геодезических систем планового и высотного обоснования используется способ наименьших квадратов. Способ используется как для уравнивания сети обоснования при выполнении съемочных работ, так и для иных геодезических измерений.

Теоретическая суть способа заключается в следующем.

Допустим, что имеет место серия измеренных параметров, функции которых определяются следующей последовательностью чисел:

X₁, X₂, X₃, …, X_n.

Каждой функции в этой последовательности соответствуют погрешности:

∆₁, ∆₂, ∆₃, …, ∆_n,

которые подчиняются закону нормального распределения и имеют свою вероятность появления. Совокупность случайных погрешностей определяется в соответствии с теоремой умножения их вероятностей. В этом случае будем иметь:

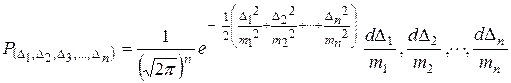, (16)

где n – количество измерений;

m – среднеквадратическая погрешность;

d∆i – дифференциал погрешности.

Анализ формулы (16) показывает, что максимальной вероятности появления совокупности распределений погрешностей в левой части уравнения, будет соответствовать наименьшее абсолютное значение показателя степени в правой части этого уравнения. То есть,

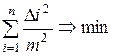. (17)

Или, если для поправок V_i поставить условие

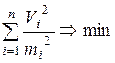, (18)

аналогичное требованию (17), то оно наилучшим образом приводит к соответствующим погрешностям измерений. Как известно весовой коэффициент измерений устанавливается формулой:

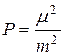, (19)

где m - произвольно выбранное число.

Подставляя (19) в (18) получим основное уравнение поправок:

å PV² Þ min, (20)

применение которого поясним на примере определения вероятнейшего значения величины X, при ее измерении с различной точностью. Так как V_i = X_ср – X_i, то, используя уравнение (20), можно записать:

f_(x) = å P_i(X_ср – X_i)² Þ min. (21)

Минимум функции (21) достигается приравниванием производной нулю и вычислением значений функции в критических точках. Дифференцируя (21) и выполнив несложные преобразования, получим уравнение, для средевесового значения:

X_ср å P_i = å P_i X_i. Или 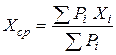(22)

Дата добавления: 2013-12-12