Функция сдвига

Второе направление связано с машинной математикой. Здесь сущность понятия алгоритма раскрывается путем рассмотрения процессов, осуществляемых в машине. Впервые это было сделано Тьюрингом, который предложил общую и вместе с тем самую простую концепцию вычислительной машины. Ее описание было дано Тьюрингом в 1937 г. А это направление в теории алгоритмов получило название - машина Тьюринга.

B

С D

А

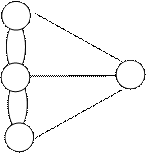Рис. 3.5 Граф «Кенигсбергские мосты»

Вершины графа (A, B, C, D) имеют степени:

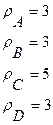(3.3)

Тогда в соответствии с теоремой Эйлера данный граф не является Эйлеровым. А это означает, что нельзя обойти все мосты г. Кенигсберга строго по одному разу, начав и закончив путь в одной точке суши.

Следствие из ТЕОРЕМЫ: Для того чтобы граф содержал Эйлеровую цепь, необходимо и достаточно, чтобы две вершины имели нечетную степень. При этом в одной из вершин цепь будет начинаться, в другой – заканчиваться.

3.3. Ядро графа.

3.3.1. Множество внутренней устойчивости графа

Множество внутренней устойчивости графа – это множество несмежных вершин.

Пусть дан граф 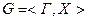. Тогда для множества внутренней устойчивости 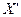справедливо следующее:

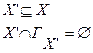(3.4)

Максимальным множеством внутренней устойчивости называется внутренне устойчивое множество, добавление любой вершины к которому, делает это множество неустойчивым.

ПРИМЕР

Дан граф

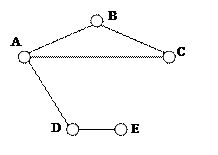
Рис. 3.6 Граф

Данный граф имеет следующие множества внутренней устойчивости.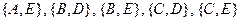

Рассмотрим множество 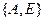. Добавляя к нему любую вершину, получаем множества внутренне неустойчивые: 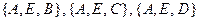. Следовательно, множество 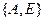является максимальным множеством внутренней устойчивости.

Числом внутренней устойчивости (α) называется число, равное наибольшей мощности максимального внутренне устойчивого множества.

Очевидно, что поиск максимальных внутренне устойчивых множеств путем простого перебора является неэффективной процедурой, поэтому для поиска максимальных внутренне устойчивых множеств существует специальный алгоритм – алгоритм Магу.

3.3.1.1. Алгоритм Магу для определения множества внутренней устойчивости графа

Пусть дан граф 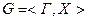. Для данного графа существует множество внутренней устойчивости .

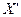Введем булевую переменную 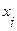, которая определяется следующим образом:

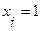, если вершина 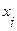принадлежит множеству внутренней устойчивости ;

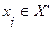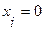, если вершина 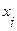не принадлежит множеству внутренней устойчивости ;

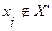Введем булевую переменную :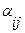

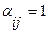, если между i-той и j-той вершиной есть дуга;

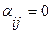, если между i-той и j-той вершиной нет дуги.

Тогда определение внутренней устойчивости (3.4) может быть представлено в следующем виде:

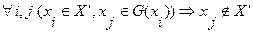(3.5)

Или используя булевую алгебру:

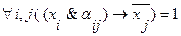(3.6)

Применяя формулы равносильности, преобразуем:

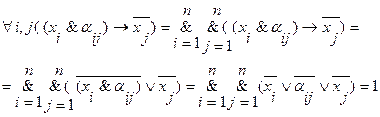(3.7)

Рассмотрим выражение:

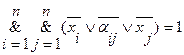(3.8)

Если 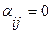, то данное равенство является тавтологией.

Если 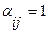, то равенство имеет вид:

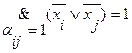(3.9)

Данное уравнение лежит в основе алгоритма Магу

Алгоритм Магу состоит из следующих этапов:

1. Для графа составляется матрица смежности.

2. По таблице смежности выписываются все парные дизъюнкции.

3. Выражение приводится к ДНФ.

4. Для любой элементарной конъюнкции выписываются недостающие элементы, которые и образуют множество внутренней устойчивости.

ПРИМЕР

Дан граф

Рис. 3.7 Граф

Матрица смежности имеет вид:

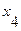
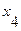
Для всех единиц выписываются парные дизъюнкции:

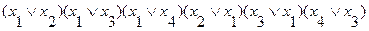(3.10)

Приведем выражение к ДНФ:

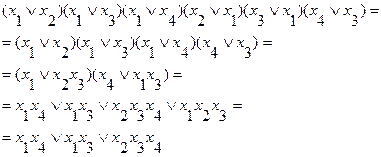(3.11)

Множества внутренней устойчивости:

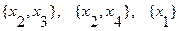
Числом внутренней устойчивости 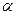= 2.

3.3.2. Множество внешней устойчивости графа

Множество внешней устойчивости – множество вершин, для которых выполняется одно из следующих правил:

1). Любая вершина входит в это множество

2) Либо вершина не входит в это множество, но из этой вершины есть дуга в данное множество.

Пусть дан граф 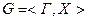. Тогда для множества внешней устойчивости 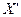справедливо следующее:

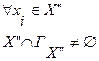(3.12)

Число внешней устойчивости (β) – это наименьшая мощность из всех множеств внешней устойчивости.

3.3.2.1. Алгоритм Магу для определения множества внешней устойчивости.

Пусть дан граф 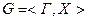. Для данного графа существует множество внешней устойчивости .

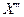Вводятся булевые переменные 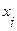и 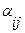по тому же правилу, что и для алгоритма Магу для определения множества внутренней устойчивости.

Тогда определение множества внешней устойчивости (3.12) запишется следующим образом:

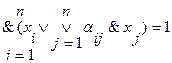(3.13)

Для 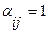справедливо следующее

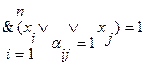(3.14)

Данное уравнение лежит в основе алгоритма Магу

Алгоритм Магу состоит из следующих этапов:

1. Для графа составляется матрица смежности

2. Матрица смежности дополняется единицами (1) по главной диагонали.

3. Для каждой строки выписываются дизъюнкции.

4. Выражение приводится к ДНФ.

5. Все вершины, входящие в элементарную конъюнкцию, образуют множество внешней устойчивости

ПРИМЕР

Определить множество внешней устойчивости для графа, представленного на рис. 3.7.

Матрица смежности имеет вид:

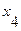
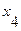
Дополним матрицу смежности единицами по главной диагонали

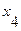
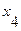
Для каждой строки выписываются дизъюнкции:

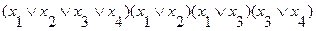(3.15)

Приведем выражение к ДНФ:

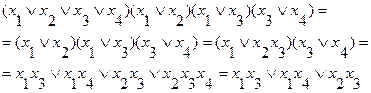(3.16)

Множества внутренней устойчивости:

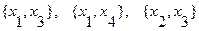
Числом внешней устойчивости 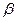= 2.

Ядром графа называется подмножество вершин, являющихся одновременно внутренней и внешней устойчивостью.

Граф, представленный на рис. 3.7. имеет ядро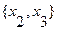

3.4. Множество путей в графе

По матрице смежности можно определить, сколько различных путей существует между i -той и j - той вершинами длиной в к единиц. Для этого необходимо определить матрицу 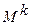, где 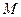- матрица смежности.

Если элемент 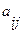матрицы :

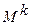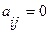- между i -той и j - той вершины не существует пути длиной в к единиц;

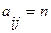- между i -той и j - той вершины существуют 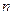различных путей длиной в к единиц;

Если 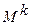- нулевая матрица, это означает, что графе нет путей в к единиц, а максимальный путь – это путь длиной в (к -1) единиц.

3.5. Минимальный путь в графе.

Одной из самых распространенных задач в теории графов является задача поиска минимального пути в графе.

Рассмотрим некоторые свойства минимальных путей

1. Любой минимальный путь является простым путем.

2. Если путь 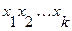- минимальный, то любые пути 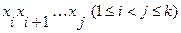внутри минимального пути также будут минимальны.

Пусть Г^-1_х – прообраз вершины x_i – это множество вершин, из которых исходят дуги в вершину x_i.

Одним из алгоритмов поиска минимального пути в графе является алгоритм фронта волны (FW –Front Wave)

3.5.1. Алгоритм фронта волны.

Пусть необходимо найти минимальный путь из вершины 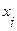в вершину .

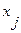1. Выписываются все вершины с 1 по n. Вершина помечается индексом 0.

2. Находится первый фронт волны 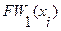как множество вершин образа вершины .

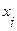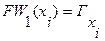(3.17)

3. Все вершины, принадлежащие первому фронту волны, помечаются индексом 1.

4. Вводится счетчик шагов (фронтов волны) .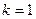

5. Ес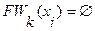ли или 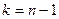, то вершина 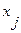недостижима из вершины, и работа алгоритма на этом заканчивается. В противном смысле переходим к пункту 6.

6. Если 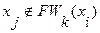, то переходим к пункту 8. В противном случае существует путь из вершины 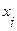в вершину 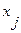длиной в 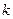единиц, и этот путь минимальный:

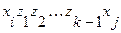
7. Находятся промежуточные вершины 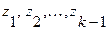z по правилу:

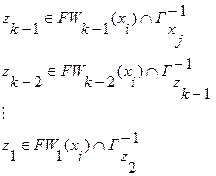, (3.18)

где 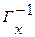- прообраз вершины 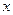- множество вершин, из которых заходят дуги в вершину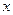

8. Определяется 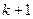фронт волны как все непомеченные вершины, принадлежащие образу вершин 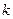- го фронта волны. Помечаются индексом 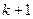вершины 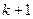фронта волны. Далее осуществляется переход к пункту 5.

ПРИМЕР

Пусть задан граф матрицей смежности:

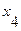
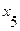
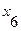
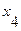
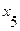
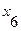
Необходимо найти минимальный путь из вершины в вершину 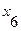(по алгоритму «фронта волны»).

1. Выпишем все вершины. Вершина помечается индексом «0»

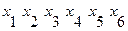
2. Находится первый фронт волны:

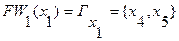
3. Все вершины, принадлежащие первому фронту волны, помечаются индексом «1».

0 1 1

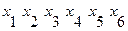
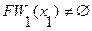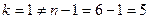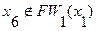4. Так как , и , то определяем второй фронт волны:

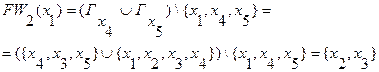
5. Все вершины, принадлежащие второму фронту волны, помечаются индексом «2».

0 2 2 1 1

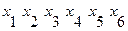
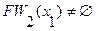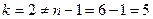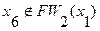6. Так как , и , то определяем третий фронт волны:

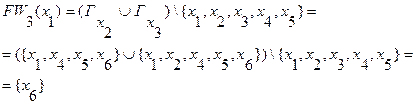
7. Так как 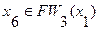, то существует путь из вершины в вершину 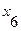длиной 3 единицы:

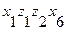
8. Находятся промежуточные вершины :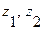

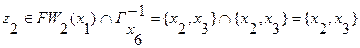
Выберем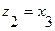

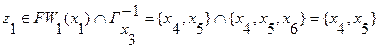
Выберем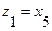

Таким образом, минимальный путь из вершины в вершину 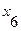имеет вид:

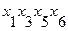
3.6. Ярусно-параллельная форма графов

Граф, не имеющий контуров, может быть представлен в ярусно-параллельной форме. Ярусно-параллельная форма – это такой вид графа, у которого в верхний нулевой ярус помещены вершины, имеющие только исходящие дуги; в нижний ярус помещены вершины, имеющие только входящие дуги. На k -том ярусе помещены вершины, которые имеют входящие дуги из предыдущих ярусов, среди которых хотя бы одна дуга из (k-1)- того яруса.

Количество вершин в ярусе определяет ширину яруса. Наибольшая ширина яруса определяет ширину графа в ярусно-параллельной форме. Количество ярусов определяет высоту графа в ярусно-параллельной форме.

3.6.1. Алгоритм приведения графа к ярусно-параллельной форме.

1. Составляется матрица смежности графа.

2. Матрица смежности просматривается в поисках нулевых столбцов. Вершины, которым соответствуют нулевые столбцы, помещаются в нулевой ярус.

3. Из матрицы смежности столбцы и строки, соответствующие вершинам нулевого яруса.

4. Повторяется п.2 данного алгоритма до тех пор, пока не будут охвачены все вершины.

5. По исходной матрице смежности восстанавливаются дуги между вершинами.

ПРИМЕР

Привести граф к ярусно-параллельной форме.

Рис. 3.8 Граф

1. Матрица смежности имеет вид:

2. В нулевой ярус помещаются вершины 3 и 8.

3. Из матрицы смежности вычеркиваются строки и столбцы, соответствующие вершинам 3 и 8:

4. В первый ярус помещаются вершины 4 и 5.

5. Из матрицы смежности вычеркиваются строки и столбцы, соответствующие вершинам 4 и 5:

6. Во второй ярус помещается вершина 1.

7. Из матрицы смежности вычеркиваются строка и столбец, соответствующие вершине 1:

8. В третий (последний) ярус помещаются вершины 2,6 и 7.

Таким образом, граф может быть представлен в ярусно-параллельной форме:

Рис. 3.9 Граф

Высота графа - 4 яруса; ширина -3.

3.7. Деревья и леса

Отделенными называются вершины, для которых не существует соединяющего эти вершины пути.

Неотделенными называются вершины, между которыми существует путь.

Подграфом графа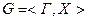называется граф вида:

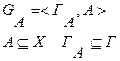(3.19)

Компонентой связности называется подграф, порождаемый множество неотделенных вершин.

ПРИМЕР

На рис. 3.10 представлен граф, имеющий две компоненты связности {1,2,3,4} и {5.6}

Рис. 3.10 Граф

Связанным графом называется граф, имеющий одну компоненту связности.

Дерево – связный неориентированный граф, в котором отсутствует цикл.

На рис. 3.11 представлены графы- деревья.

Рис. 3.11 Граф

Лесом называетсяграф, имеющий несколько компонентов связности, причем каждая из компонент является деревом.

Цикломатическим числом (g) графа называется минимальное количество ребер, которое необходимо изъять из графа, чтобы он стал деревом. Цикломатическое число определяется по формуле:

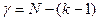, (3.20)

где N – количество ребер,

k – количество вершин.

3.7.1. Алгоритм получения дерева из графа

1. Выбирается любая вершина. Счетчик i принимаем равным 1 (i=1).

2. Если i = k, то дерево построено.

3. Если i ¹ k, то выбирается любая незадействованная вершина и ребро, соединяющее данную вершину с любой из выбранных.

4. Счетчик увеличивается на единицу.(i= i+1).

5. Переход на пункт 2.

ПРИМЕР

Преобразовать граф, представленный на рис. 3.12 в дерево:

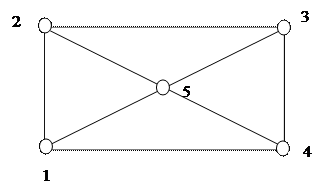Рис. 3.12

1. Найдем цикломатическое число 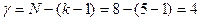, т.е. необходимо изъять 4 ребра.

2. Выбираем вершину 5.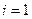

3. Присоединяем вершину 3.

4.

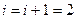
5. Присоединяем вершину 4.

6.

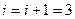
7. Присоединяем вершину 1.

8.

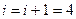
9. Присоединяем вершину 2.

10.

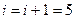
11. Все вершины охвачены. Дерево построено

Рис. 3.13

4. ТЕОРИЯ АЛГОРИТМОВ

Алгоритм – это точное, понятное предписание о том, какие действия и в каком порядке должны быть выполнены, чтобы решить любую задачу из класса однотипных задач.

Алгоритм обладает следующими характеристиками:

1. Дискретность. Алгоритм – это процесс последовательного построения величин таким образом, что в начальный момент задается исходная конечная система величин, а в каждый следующий момент система величин получается по определенному закону из системы, имевшихся в предыдущий момент времени.

2. Детерминированность. Система величин, получаемых в какой-то не начальный момент, однозначно определяется системой величин, полученных в предшествующие моменты времени.

3. Элементарность шагов алгоритмов. Закон получения последующей системы величин из предшествующих должен быть простым.

4. Массовость алгоритма. Начальная система величин может выбираться из некоторых потенциально бесконечного множества. Иначе говоря, алгоритм должен обеспечивать решение некоторому множеству (классу) задач с различными параметрами(коэффициентами).

5. Результативность алгоритма. Последовательный процесс построения величин должен быть конечным и давать результат, того есть решение задачи.

Основная задача теории алгоритмов – это решение проблемы алгоритмическойразрешимости, а не поиск правила (способа/метода) ее решения. Теория алгоритмов дает ответ на вопрос «Данная задача имеет решение?», и не отвечает на вопрос «Как решается данная задача?»

В рамках такого подхода к определению понятия алгоритма можно определить три основных направления:

1. Первое направление связано с уточнением понятия эффективно вычисляемой функции. В результате был выделен класс так называемых рекурсивных функций.

3. Третье направление связано с понятием нормальных алгоритмов, введенным и разработанным российским математиком А. А. Марковым. х Нормальные алгоритмы Маркова. Это направление получило название нормальные алгоритмы Маркова.

4.1. Рекурсивная функция

Основные понятия: элементарные функции, правила образования новых функций.

Простейшие функции:

1. Функция сохранения нуля (нуль-функция)

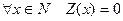(4.1)

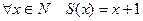(4.2)

Дата добавления: 2013-12-12