Программа машины Тьюринга (Р) - совокупность всех команд, Программа представляется в виде таблицы и называется Тьюринговой функциональной схемой

	a0	a1	a2
q1	а0Пq1	a1Пq1	a2Лq2
q2	а1Пq2	a2Нq0	a0Нq0

Таким образом, машина Тьюринга может быть представлена в виде четверки:

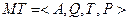(4.9)

4.2.1. Работа машины Тьюринга

Информация, хранящаяся на ленте, является набором символов из внешнего алфавита. Начальное состояние управляющей головки характеризуется символом внутреннего алфавита 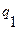. Работа машины складывается из тактов. В течение любого такта машина Тьюринга осуществляет следующие действия: машина Тьюринга находится во внутреннем состоянии 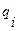, считывает входной символ 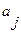и по таблице работы совершает операцию сдвига 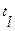, переходя в состояние 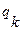, при этом входное слово 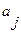заменяется на :

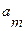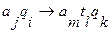
Если в результате операции машина перейдет в состояние 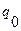, то работа машины останавливается. Если состояние 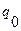недостижимо, то значит по данному входному слову машина Тьюринга не достигает конечного состояния и алгоритма для данного входного слова не существует.

ПРИМЕР

Построить машину Тьюринга, которая будет стирать последнюю единицу в последовательности единиц.

Внешний алфавит - 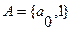. Внутренний алфавит -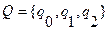, при этом состояние 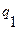.сохраняется до тех пор, пока не будет найден конец последовательности единиц, состояние 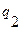- стирание последней единицы. При этом следует заметить, что ситуация 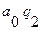в работе машины Тьюринга невозможна, поэтому соответствующая клеточка доопределена произвольно, например 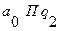. Начальное состояние 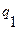на начале последовательности единиц. Рабочая программа машины Тьюринга имеет вид:

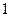
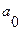
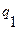
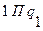
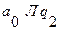
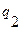
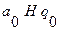
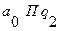
Проверим работоспособность машины Тьюринга:

1.

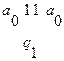
2.

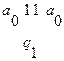
3.

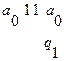
4.

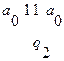
5.

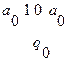
Тезис А. Черча. Если функция выполнима, то она всегда может быть представлена в виде машины Тьюринга.

4.3. Нормальные алгоритмы Маркова

Нормальный алгоритм Маркова представляет собой систему подстановок

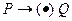, (4.10)

где 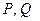- слова из символов входного алфавита

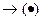- оператор подстановки, при этом:

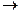-простая подстановка

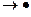- заключительная подстановка.

Слово z считается включенным в слово у, если у может быть представлено как:

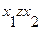, (4.11)

где 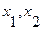- любые символы входного алфавита.

4.3.1. Работа нормального алгоритма Маркова

Исходное слово просматривается слева направо с целью выявления вхождения первого правила подстановки. Как только находится первое вхождение первого правила подстановки, оно заменяется по этому правилу и исходное слово снова просматривается с первого символа по первому правилу подстановки.

После того, как первое правило больше не встречается в данном слове, аналогично применяется второе правило подстановки.

Работа алгоритма заканчивается тогда, когда ни одна из подстановок не применима, либо использована заключительная подстановка.

ПРИМЕР

Построить нормальный алгоритм Маркова, стирающий последовательность единиц.

Нормальный алгоритм Маркова для данной задачи представляет собой две подстановки:

1.

2.

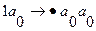
Первая подстановка стирает все единицы до последней. Вторая (заключительная) подстановка заменяет последнюю единицу пробелом .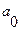

Тезис А. Черча. Если функция выполнима, то она может быть представлена в виде нормального алгоритма Маркова.

Заключительный тезис А. Черча. Если функция выполнима, то она может быть представлена в виде либо общерекурсивной функции, либо. машины Тьюринга, либо в виде нормального алгоритма Маркова.

5. ТЕОРИЯ АВТОМАТОВ

Автомат – дискретный преобразователь информации, который на основе входных сигналов, поступающих в дискретные моменты времени, и с учетом своего состояния вырабатывает выходные сигналы и изменяет свое состояние.

В данном разделе рассматриваются абстрактные автоматы, т.е. некоторая математическая модель. Вопросы практической реализации не рассматриваются. В связи с этим при построении автоматов будем иметь в виду, что:

1. Автомат функционирует в абстрактном времени.

2. Все переходы происходят мгновенно.

Автомат представляет собой кортеж 6 –го порядка:

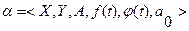, (5.1)

где 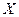– множество входных сигналов (входной алфавит),

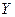– множество выходных сигналов (выходной алфавит),

– множество внутренних состояний,

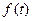– функция перехода,

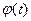– функция выхода,

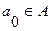- начальное состояние автомата.

5.1. Законы функционирования автоматов.

В зависимости от законов функционирования различают 3 вида автоматов:

1. Автоматы первого рода, или автоматы Мили:

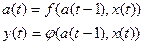(5.2)

2. Автоматы второго рода

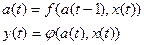(5.3)

3. Правильные автоматы второго рода, или автоматы Мура:

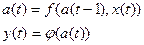(5.4)

На практике наибольшее распространение получили автоматы Мили и автоматы Мура.

5.2. Задание автоматов

Автоматы могут быть заданы следующими способами:

1. В виде графа

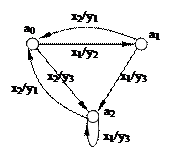
РИС. 5.1. Автомат Мили

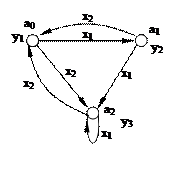
РИС. 5.2. Автомат Мура.

При построении автомата Мили каждая дуга, соединяющая вершины 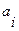и 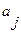, имеет обозначение 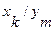. Это означает следующее: находясь, в состоянии 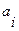автомат, отрабатывая входной сигнал 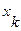, выдает выходной сигнал 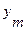и переходит в состояние .

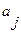Так как в автомате Мура выходной сигнал 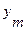зависит только от текущего состояния 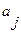, то каждая дуга, соединяющая вершины 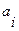и 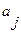, имеет обозначение .

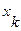2. В виде таблиц перехода и выхода (автомат Мили); отмеченной таблицы перехода (автомат Мура).

Автомат Мили описывается с помощью двух таблиц: таблицы перехода и таблицы выхода:

Таблица переходов (ТП) Таблица выходов (ТВ)

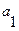
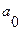
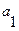
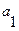
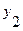
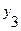
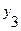
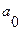
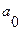
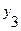
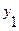
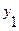
Автомат Мура описывается с помощью отмеченной таблицы перехода:

Таблица переходов (ТП)

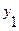
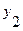
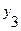
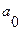
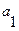
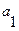
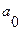
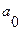
ПРИМЕР.

Синтезировать автомат, на вход которого подаются монеты номинальной стоимостью 1, 2 и 3 копейки, а на выходе автомат выдает билет, если сумма набранных монет составляет 3 копейки, если сумма меньше 3 копеек, то автомат ничего не выдает, если сумма больше 3 копеек, то автомат возвращает деньги.

Определим входной, выходной алфавиты и множество внутренних состояний:

· входной алфавит 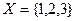- монеты номинальной стоимостью 1, 2 и 3 копейки

· выходной алфавит 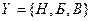- на выходе возможны выходные символы: 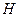- ничего;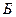- билет;- возврат.

· множество внутренних состояний ,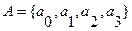

где 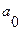- начальное состояние автомата «в автомате ничего нет»;

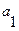- «в автомате 1 копейка»;

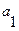- «в автомате 1 копейка»;

- «в автомате 2 копейки»;

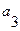- «в автомате 3 копейки».

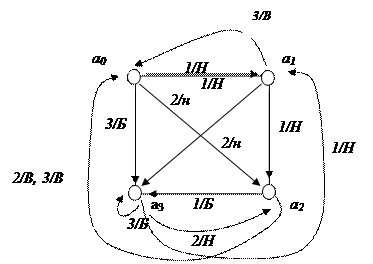Граф автомата имеет вид:

РИС. 5.3. Автомат Мили

Таблицы перехода и выхода представлены в виде:

Таблица переходов (ТП) Таблица выходов (ТВ)

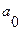
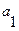
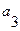
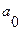
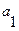
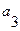
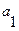
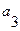
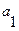
							Н	Н	Б	Н
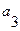
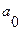
							Н	Б	В	Н
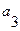
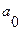
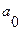
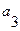
							Б	В	В	Б

Неопределенным состоянием называется несуществующее состояние.

Частичным автоматом называется автомат, в котором некоторые состояния в таблице перехода не определены. Для дальнейшего исследования неопределенное состояние некоторым образом доопределяют.

5.3. Минимизация автоматов

Входным словом называется совокупность сигналов, поступающих на вход.

Выходным словом называются совокупность сигналов на выходе.

Два автомата называются эквивалентными, если они имеют одинаковый входной и выходной алфавит, и на одинаковые входные слова выдают одинаковые выходные слова.

Два состояния одноэквивалентными, если на одинаковое входное слово выдается одинаковый выходной сигнал.

Два состояния k-эквивалентными, если на одинаковое входное слово длиной в k-единиц выдается одинаковый выходной сигнал длиной в k-единиц.

Эквивалентными состояниями называются k-эквивалентные состояния для любых k.

Эквивалентные состояния объединяются в класс эквивалентности.

Минимальный автомат – это автомат, состоящий из наименьшего числа состояний, каждое из которых является классом эквивалентности исходного автомата.

5.3.1. Алгоритм минимизации автомата Мили

1. По таблице выхода находятся состояния с одинаковыми выходными сигналами. Данные состояния объединяются в класс одноэквивалентных состояний. Проводится перекодировка.

2. По таблице перехода определяются классы двухэквивалентных состояний: для любого класса выделяется состояние, которое на одинаковый входной сигнал переходит в одинаковое состояние. Объединяем двухэквивалентные состояния в классы двухэквивалентных состояний. Проводится перекодировка.

3. Алгоритм выполняется, пока в классах k-эквивалентных состояний не находятся одинаковые состояния.

4. Вводятся новые состояния, соответствующие классам эквивалентных состояний.

5. С учетом новых состояний переписываются таблицы перехода и выхода.

ПРИМЕР

Пусть задан автомат Мили

Таблица выходов

Таблица переходов

Определяем класс одноэквивалентных состояний по таблице выхода

Таблица выходов

	а	в	а	в	а	в	а	в

Выделяются два класса одноэквивалентных состояний a ={1,3,5,7,8} и b ={2,4,6,9}. Перегруппируем таблицу перехода по классам одноэквивалентных состояний

Таблица переходов

	а	в

Перекодируем состояния по полученным классам

Таблица переходов

	а	в
	2/в	2/в	6/в	6/в	4/в	1/а	3/а	8/а	7/а
	2/в	2/в	4/в	2/в	4/в	4/в	2/в	9/в	9/в
	5/а	5/а	3/а	8/а	7/а	4/в	2/в	6/в	7/а

Выделяем внутри каждого из классов одинаковые состояния, тем самым определяя классы двухэквивалентных состояний

Таблица переходов

	а	в
	2/в	2/в	6/в	6/в	4/в	1/а	3/а	8/а	7/а
	2/в	2/в	4/в	2/в	4/в	4/в	2/в	9/в	9/в
	5/а	5/а	3/а	8/а	7/а	4/в	2/в	6/в	7/а
	а	в	с

Определим новые классы двухэквивалентных состояний a ={1,3,5,7,8}, b ={2,4,6}, c ={9}, перекодируем по новым состояниям и выделим классы трехэквивалентных состояний

Таблица переходов

	а	в	с
	2/в	2/в	6/в	6/в	4/в	1/а	3/а	8/а	7/а
	2/в	2/в	4/в	2/в	4/в	4/в	2/в	9/с	9/с
	5/а	5/а	3/а	8/а	7/а	4/в	2/в	6/в	7/а
	а	в	с	d

Классы трехэквивалентных состояний a ={1,3,5,7,8}, b ={2,4}, c ={6}, d ={9} перекодируем по новым состояниям и выделим классы четырехэквивалентных состояний

Таблица переходов

	а	в	с	d
	2/в	2/в	6/с	6/с	4/в	1/а	3/а	8/а	7/а
	2/в	2/в	4/в	2/в	4/в	4/в	2/в	9/d	9/d
	5/а	5/а	3/а	8/а	7/а	4/в	2/в	6/с	7/а
	а	в	а	c	d	e

Перегруппируем таблицу перехода по новым классам a ={1,3,8}, b ={5,7}, c ={2,4}, d ={6}, е ={9}, перекодируем по новым состояниям.

Таблица переходов

	а	в	c	d	e
	2/с	2/с	4/с	6/d	6/ d	1/a	3/a	8/a	7/b
	2/с	2/с	4/с	4/c	2/c	4/c	2/c	9/e	9/e
	5/в	5/в	7/в	3/a	8/a	4/c	2/c	6/d	7/b
	а	в	c	d	e

Так как внутри из каждого класса дальнейшее разбиение на классы не осуществляется, это означает, что найдены классы эквивалентных состояний :. a ={1,3,8}, b ={5,7}, c ={2,4}, d ={6}, е ={9}.

Минимизированный автомат Мили в новых состояниях имеет вид

Таблица переходов

	a	b	c	d	e
	с	d	a	a	b
	с	c	c	e	e
	в	c	c	d	b

Таблица выходов

	a	b	c	d	e
	1	1	0	0	0
	0	0	1	0	0
	0	0	1	1	1

5.3.2. Особенности минимизации автомата Мура.

:

Автомат Мура минимизируется аналогично минимизации автомата Мили за исключением первого шага. Выделение класса одноэквивалентных состояний осуществляется по строке выходов отмеченной таблицы переходов автомата Мура.

5.3.3. Минимизация частичных автоматов.

Для того, чтобы провести минимизацию частичных автоматов неопределенное состояние доопределяется самостоятельно. Далее минимизация автоматов осуществляется по вышеизложенному алгоритму.

5.4. Переход от автомата Мили к автомату Мура

Автоматы Мили и автоматы Мура отличаются функцией выхода.

Автомат Мили:

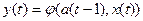(5.5)

Автомат Мура:

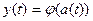(5.6)

То есть произвольному состоянию автомата Мили 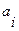и входному сигналу 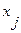соответствует состояние 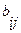автомата Мура:

(5.7)

При этом начальные состояния автоматов Мили и Мура совпадают:

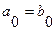(5.8)

Учитывая вышеизложенное, можно перекодировать таблицу перехода автомата Мили и составить отмеченную таблицу переходов автомата Мура.

ПРИМЕР

Пусть задан автомат Мили

Таблица переходов (ТП) Таблица выходов (ТВ)

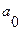
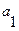
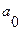
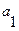
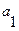
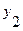
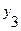
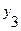
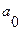
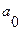
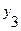
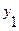
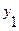
Перекодируем матрицу перехода автомата Мили:

	/	/	/
	/	/	/

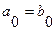
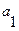
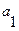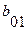
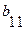
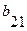
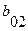
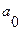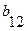
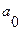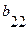
Составляем таблицу перехода автомата Мура.

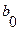
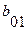
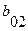
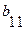
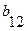
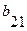
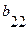
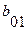
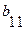
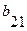
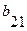
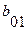
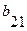
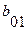
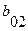
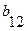
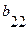
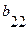
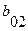
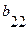
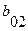
При составлении таблицы перехода автомата Мили рассуждаем следующим образом: состояние автомата Мура 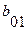соответствует состоянию автомата Мили 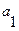, следовательно, столбец состояния 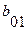автомата Мура совпадает со столбцом состояния 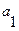автомата Мили.

Так как в автомате Мура произвольному состоянию 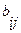соответствует некоторый выходной сигнал, то строка выхода отмеченной таблицы перехода автомата Мура однозначно определяется таблицей выхода автомата Мили (состоянию 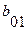соответствует выходной сигнал ; - )

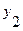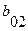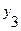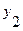
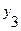
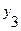
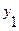
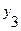
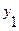
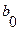
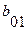
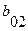
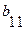
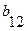
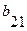
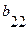
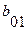
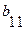
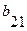
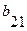
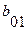
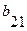
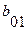
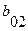
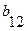
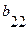
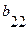
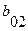
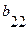
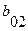
Выходной сигнал, соответствующий состоянию 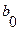, выбирается произвольно.

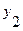
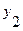
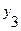
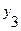
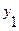
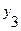
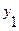
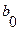
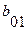
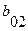
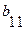
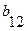
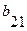
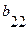
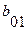
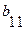
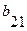
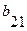
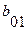
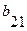
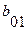
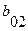
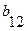
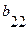
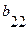
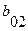
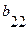
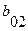
Если автомат Мили содержит m -состояний и n входных символов, то количество состояний автомата Мура определяется по формуле:

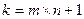(5.9)

5.5. Переход от автомата Мура к автомату Мили

Переход от автомата Мура к автомату Мили заключается в построении таблицы выходов. Построение состоит в подстановке выходных сигналов, отмечающих состояния в отмеченной таблице переходов, вместо состояний, в которые автомат переходит. Тем самым, если говорить в терминах графов, выходные сигналы от состояний переносятся на дуги, которые в эти состояния заходят.

А таблица переходов автомата Мили получается из отмеченной таблицы переходов автомата Мура отбрасыванием строки выходов.

ПРИМЕР

Пусть задан автомат Мура в виде отмеченной таблицы перехода

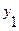
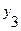
	A	B	C
	A	B	A
	B	B	C
	C	A	C

Данный автомат может быть представлен в виде графа:

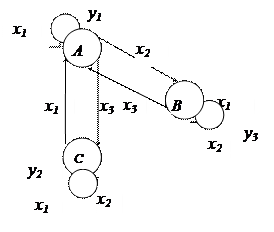РИС. 5.4. Автомат Мура

Автомат Мили будет иметь вид:

· в виде таблиц перехода и выхода

Таблица переходов Таблица выходов

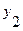
	A	B	C			A	B	C
	A	B	A
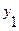
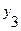
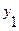
	B	B	C
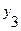
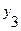
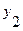
	C	A	C

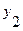
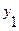
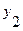
· в виде графа

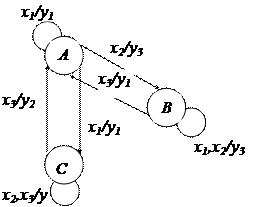РИС. 5.5. Автомат Мили

6. КОМБИНАТОРИКА

6.1. Основные понятия.

Дата добавления: 2013-12-12