Курс лекций

Пример

Пример

Пример

Пример

Пример

Пример.

Пример.

Пример.

Биномиальная теорема.

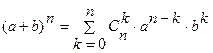(6.14)

Доказательство.

Перемножим последовательно (a+b) n раз. Получим сумму 2n слагаемых вида d1d2...dn, где di (i=1,…,n) равно либо a, либо b. Разобьем все слагаемые на n+1 группу B0,B1,…,Bn, относя к группе Bk все те произведения, в которых b встречается множителем k раз, а a — n–k раз. Число элементов в Bk очевидно равно 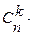(таким числом способов среди n произведений d1d2...dn можно выбрать k сомножителей, равных b), а каждый элемент в Bk равен 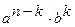. Отсюда и получаем формулу (6.14).

Используя биномиальную теорему, получить формулу для расчета 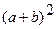и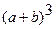

Решение.

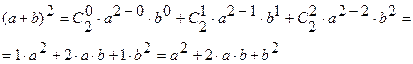
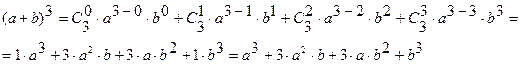
7. НЕЧЕТКИЕ МНОЖЕСТВА

7.1. Введение

Пожалуй, наиболее поразительным свойством человеческого интеллекта является способность принимать правильные решения в обстановке неполной и нечеткой информации. Построение моделей приближенных рассуждений человека и использование их в компьютерных системах будущих поколений представляет сегодня одну из важнейших проблем науки.

Значительное продвижение в этом направлении сделано 30 лет тому назад профессором Калифорнийского университета (Беркли) Лотфи А. Заде (Lotfi A. Zadeh). Его работа "Fuzzy Sets", появившаяся в 1965 году в журнале Information and Control, № 8, заложила основы моделирования интеллектуальной деятельности человека и явилась начальным толчком к развитию новой математической теории.

Что же предложил Заде? Во-первых, он расширил классическое канторовское понятие множества, допустив, что характеристическая функция (функция принадлежности элемента множеству) может принимать любые значения в интервале (0;1), а не только значения 0 либо 1. Такие множества были названы им нечеткими (fuzzy). Л.Заде определил также ряд операций над нечеткими множествами и предложил обобщение известных методов логического вывода modus ponens и modus tollens.

Введя затем понятие лингвистической переменной и допустив, что в качестве ее значений (термов) выступают нечеткие множества, Л.Заде создал аппарат для описания процессов интеллектуальной деятельности, включая нечеткость и неопределенность выражений.

Дальнейшие работы профессора Л.Заде и его последователей заложили прочный фундамент новой теории и создали предпосылки для внедрения методов нечеткого управления в инженерную практику.

7.2. Основные определения.

Подход к формализации понятия нечеткого множества состоит в обобщении понятия принадлежности. В обычной теории множеств существует несколько способов задания множества. Одним из них является задание с помощью характеристической функции, определяемой следующим образом.

Пусть 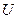— так называемое универсальное множество, из элементов которого образованы все остальные множества, рассматриваемые в данном классе задач, например множество всех целых чисел, множество всех гладких функций и т.д.

Характеристической функцией множества 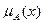называется функция, значения которой указывают, является ли 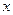элементом множества :

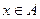(7.1)

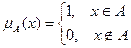(7.2)

Особенностью этой функции является бинарный характер ее значений.

С точки зрения характеристической функции, нечеткие множества есть естественное обобщение обычных множеств, когда мы отказываемся от бинарного характера этой функции и предполагаем, что она может принимать любые значения на отрезке .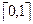

В теории нечетких множеств характеристическая функция называется функцией принадлежности, а ее значение 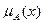— степенью принадлежности элемента 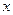нечеткому множеству .

Нечетким множеством называется совокупность пар

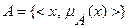(7.3)

Пусть универсум 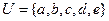, а множество задано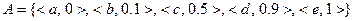

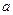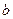Тогда, очевидно, что элемент не принадлежит множеству , элемент принадлежит ему в малой степени, элемент 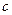более или менее принадлежит, элемент 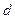принадлежит в значительной степени, 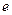является элементом множества .

Пусть универсум 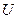есть множество действительных чисел. Нечеткое множество , обозначающее множество чисел, близких к 10, можно задать следующей функцией принадлежности:

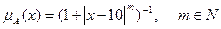
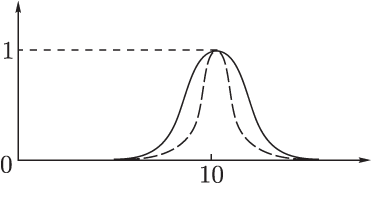
Рис. 7.1.

Показатель степени 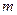выбирается в зависимости от степени близости к 10. Так для описания множества чисел, очень близких к 10, можно положить 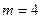; для множества чисел, не очень далеких от 10, .

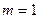Для описания множеств, представляющих собой некоторые понятия или качества, вводится понятие лингвистической переменной. Лингвистическая переменная - это переменная, значениями которой являются не числа, а слова или предложения естественного (или формального) языка.

Лингвистическая переменная "возраст" может принимать следующие значения: "очень молодой", "молодой", "среднего возраста", "старый", "очень старый" и др. Ясно, что переменная "возраст" будет обычной переменной, если ее значения — точные числа; лингвистической она становится, будучи использованной в нечетких рассуждениях человека.

Каждому значению лингвистической переменной соответствует определенное нечеткое множество со своей функцией принадлежности. Так, лингвистическому значению "молодой" может соответствовать функция принадлежности, изображенная на рис. 7.2.

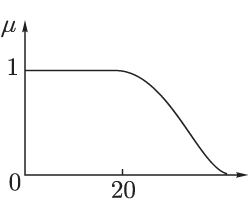
Рис. 7.2.

7.3. Операции над нечеткими множествами.

Над нечеткими множествами можно производить различные операции, при этом необходимо определить их так, чтобы в частном случае, когда множество является четким, операции переходили в обычные операции теории множеств, то есть операции над нечеткими множествами должны обобщать соответствующие операции над обычными множествами. При этом обобщение может быть реализовано различными способами, из-за чего какой-либо операции над обычными множествами может соответствовать несколько операций в теории нечетких множеств.

Пусть и - нечеткие множества.

Множество является подмножеством множества 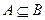, если:

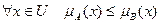(7.4)

Если - множество чисел, очень близких к 10, а - множество чисел, близких к 10, то .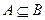

Два нечетких множества и равны тогда и только тогда, когда равны их функции принадлежности.

Объединением 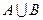нечетких множеств и называется наименьшее нечеткое подмножество, включающее как , так и , с функцией принадлежности

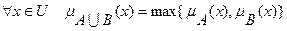(7.5)

Пересечением 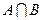нечетких множеств и называется наибольшее нечеткое подмножество, содержащееся одновременно в и , с функцией принадлежности

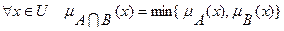(7.6)

Разностью 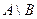нечетких множеств и называется нечеткое множество с функцией принадлежности

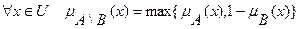(7.7)

Дополнением нечеткого множеств и называется нечеткое множество 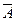, функция принадлежности которого определяется следующим образом:

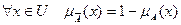(7.8)

Дизъюнктивной суммой 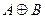нечетких множеств и называется нечеткое множество с функцией принадлежности

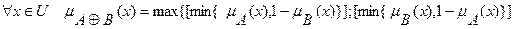(7.9)

Пусть заданы множества и :

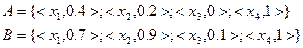
Очевидно, что .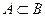

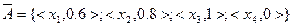
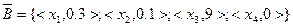
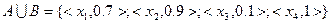
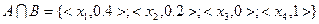
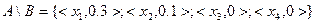
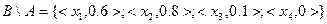
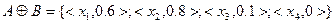
7.3. Наглядное представление операций над нечеткими множествами.

Наглядное представление основных операций представлено следующим образом.

На рисунке рассматривается прямоугольная система координат, на оси ординат которой откладываются значения 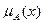, на оси абсцисс в произвольном порядке располагаются элементы 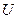. Если 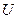по своей природе упорядочено, то этот порядок желательно сохранить в расположении элементов на оси абсцисс.

Рис. 7.3. Нечеткое множество

На рис 7.3 заштрихованная часть соответствует нечеткому множеству .

Рис. 7.4. Нечеткое множество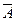

Рис. 7.5. Нечеткое множество

Рис. 7.6. Нечеткое множество

Пример.

Пусть - нечеткое множество "от 5 до 8") и - нечеткое множество "около 4", заданные своими функциями принадлежности:

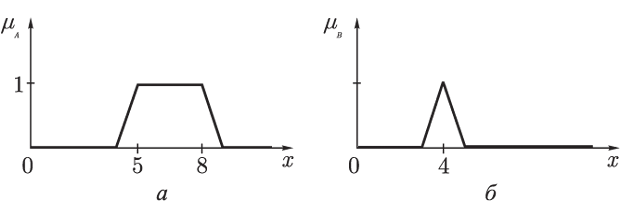
Рис. 7.7.

Тогда, операции пересечения, объединения и дополнения могут быть представлены следующим образом:

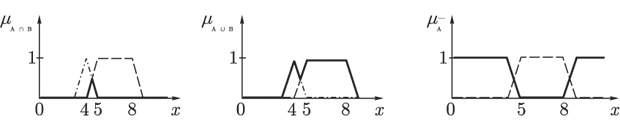
Рис. 7.8.

7.4. Свойства основных операций над нечеткими множествами.

Пусть А, В, С - нечеткие множества, тогда выполняются следующие свойства:

15. Коммутативный закон

(7.8)

16. Ассоциативный закон

(7.9)

17. Дистрибутивный закон

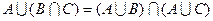
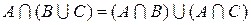(7.10)

18. Закон де Моргана

(7.11)

19. Закон идемпотентности

(7.12)

20. Операции с пустым множеством:

, (7.13)

где 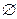- пустое множество с функцией принадлежности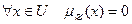

21. Операции с универсумом:

(7.14)

22. Представление разности через объединение и дополнение

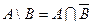(7.15)

23. Представление дизъюнктивной суммы через объединение и дополнение

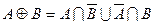(7.16)

В отличие от четких множеств, для нечетких множеств в общем случае:

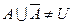(7.17)

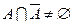(7.18)

7.5. Алгебраические операции над нечеткими множествами.

Алгебраическим произведением 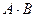нечетких множеств и называется нечеткое множество, функция принадлежности которого определяется следующим образом:

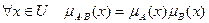(7.19)

Алгебраической суммой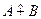 нечетких множеств и называется нечеткое множество, функция принадлежности которого определяется следующим образом:

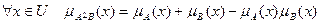(7.20)

Для операций 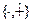выполняются свойства:

1. Коммутативный закон

(7.21)

2. Ассоциативный закон

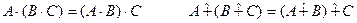(7.22)

3. Закон де Моргана

(7.23)

4. Операции с пустым множеством:

, (7.24)

5. Операции с универсумом:

(7.25)

Не выполняются следующие свойства:

1. Дистрибутивный закон

(7.26)

2. Закон идемпотентности

(7.27)

3. Закон исключенного третьего

(7.28)

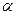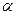На основе операции алгебраического произведения определяется операция возведения в степень нечеткого множества , где - положительное число. Нечеткое множество 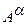определяется функцией принадлежности:

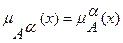(7.29)

Частным случаем возведения в степень являются операции концентрирования 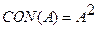и растяжения 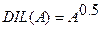, которые используются при работе с лингвистическими неопределенностями. Наглядное представление этих операций представлено на рис 7.9.

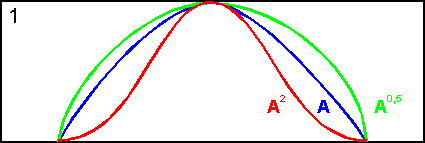
Рис. 7. 9.

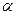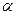Умножением на число , где - положительное число такое, что 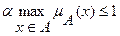, называется нечеткое множество 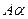с функцией принадлежности:

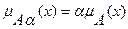(7.30)

Пусть даны нечеткие множества универсального множества 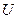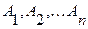и неотрицательные числа 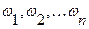, сумма которых равна 1. Выпуклой комбинацией нечетких множеств 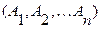называется нечеткое множество с функцией принадлежности:

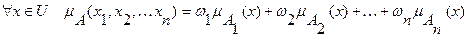(7.31)

Декартовым произведением нечетких множеств 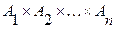, каждое из которых является подмножеством соответствующего универсального множества 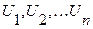, называется нечеткое множество, являющееся подмножеством универсального множества 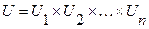, с функцией принадлежности:

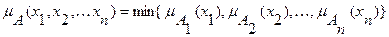(7.32)

Оператор увеличения нечеткости используется для преобразования четких множеств в нечеткие и для увеличения нечеткости нечеткого множества.

Пусть - нечеткое множество, 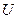- универсальное множество и для всех 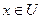определены нечеткие множества 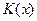. Совокупность всех 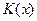называется ядром оператора увеличения нечеткости Ф. Результатом действия оператора Ф на нечеткое множество A является нечеткое множество вида:

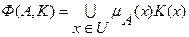, (7.33)

где 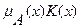- произведение числа на нечеткое множество.

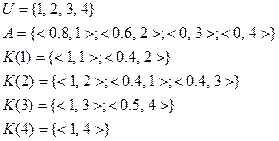
Тогда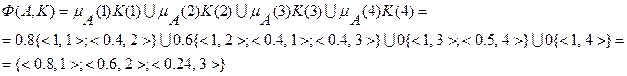

8. Нечеткая логика.

Нечеткая логика это обобщение традиционной логики на случай, когда истинность рассматривается как лингвистическая переменная, принимающая значения типа: "очень истинно", "более-менее истинно", "не очень ложно" и т.п. Указанные лингвистические значения представляются нечеткими множествами.

8.1. Лингвистические переменные

Лингвистической переменной называется переменная, принимающая значения из множества слов или словосочетаний некоторого естественного или искусственного языка.

Терм-множеством называется множество допустимых значений лингвистической переменной.

Задание значения переменной словами, без использования чисел, для человека более естественно. Ежедневно мы принимаем решения на основе лингвистической информации типа: "очень высокая температура"; "длительная поездка"; "быстрый ответ"; "красивый букет"; "гармоничный вкус" и т.п. Психологи установили, что в человеческом мозге почти вся числовая информация вербально перекодируется и хранится в виде лингвистических термов. Понятие лингвистической переменной играет важную роль в нечетком логическом выводе и в принятии решений на основе приближенных рассуждений. Формально, лингвистическая переменная определяется следующим образом.

Лингвистическая переменная задается пятеркой 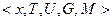, где 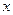- имя логической переменной; 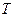- терм-множество, каждый элемент которого (терм) представляется как нечеткое множество на универсальном множестве 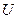; 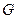- синтаксические правила, часто в виде грамматики, порождающие название термов; 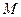- семантические правила, задающие функции принадлежности нечетких термов, порожденных синтаксическими правилами .

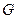Рассмотрим лингвистическую переменную с именем 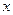- температура в комнате".

Тогда универсальное множество 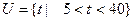. Терм-множество 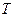можно определить как 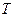={"холодно", "комфортно", "жарко"} с следующими функциями принадлежности:

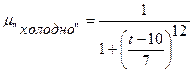
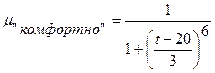
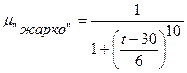
Множество синтаксических правил 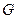, порождающее новые термы с использованием квантификаторов {"не", "очень" и "более-менее"};

Семантические правила 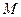заданы в виде таблицы расчета функций принадлежности

Квантификатор	Функция принадлежности
не t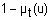
очень t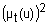
более-менее t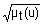

Графики функций принадлежности термов "холодно", "не очень холодно", "комфортно", "более-менее комфортно", "жарко" и "очень жарко" лингвистической переменной "температура в комнате" показаны на рис. 8.1.

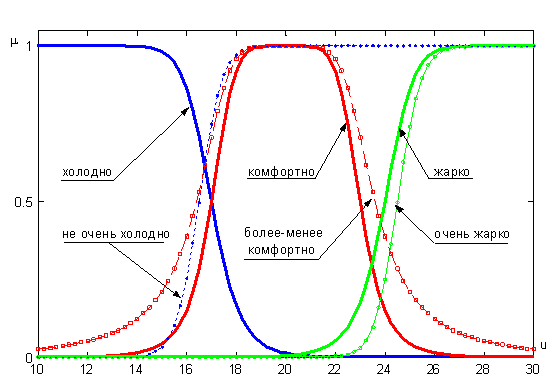
Рис. 8.1- Лингвистическая переменная "температура в комнате"

8.2. Нечеткая истинность

Особое место в нечеткой логике занимает лингвистическая переменная "истинность". В классической логике истинность может принимать только два значения: истинно и ложно. В нечеткой логике истинность "размытая". Нечеткая истинность определяется аксиоматически, причем разные авторы делают это по-разному.

Для задания нечеткой истинности Заде предложил такие функции принадлежности термов "истинно" и "ложно":

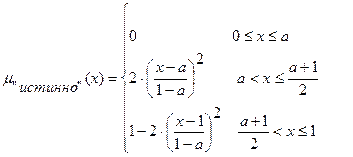(8.1)

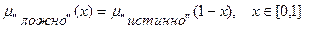, (8.2)

где 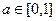- параметр, определяющий носители нечетких множеств "истинно" и "ложно".

Для нечеткого множества «истинно» носителем будет интервал 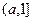, а для нечеткого множества «ложно» - .

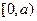Функции принадлежности нечетких термов «истинно» и «ложно» изображены на рис. 8.2. Они построены при значении параметра 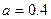. Как видно, графики функций принадлежности термов «истинно» и «ложно» представляют собой зеркальные отображения.

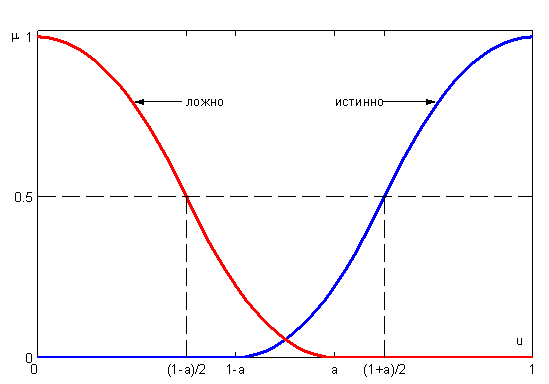
Рис. 8.2 Лингвистическая переменная «истинность» по Заде

Для задания нечеткой истинности Балдвин предложил такие функции принадлежности нечетких "истинно" и "ложно":

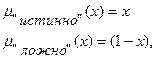(8.3)

где .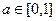

Квантификаторы "более-менее" и "очень" часто применяют к нечеткими множествами "истинно" и "ложно", получая таким образом термы "очень ложно", "более-менее ложно", "более-менее истинно", "очень истинно", "очень, очень истинно", "очень, очень ложно" и т.п. Функции принадлежности новых термов получают, выполняя операции концентрации и растяжения нечетких множеств "истинно" и "ложно". Операция концентрации соответствует возведению функции принадлежности в квадрат, а операция растяжения - возведению в степень ½.

Следовательно, функции принадлежности термов "очень, очень ложно", "очень ложно", "более-менее ложно", "более-менее истинно", "истинно", "очень истинно" и "очень, очень истинно" задаются так:

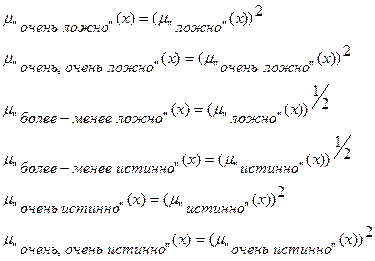(8.4)

Графики функций принадлежности этих термов показаны на рис. 8.3.

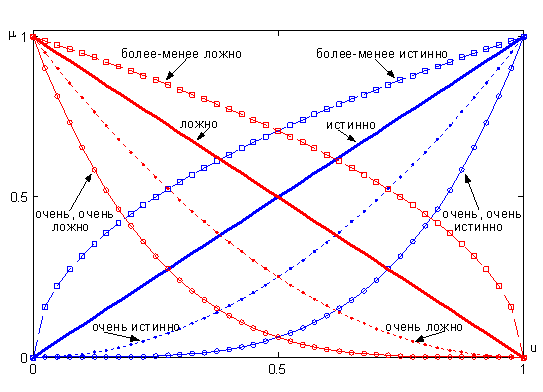
Рис. 8.3 Лингвистическая переменная "истинность" по Балдвину.

8.3. Нечеткие логические операции

Вначале кратко напомнить основные положения булевой логики. Рассмотрим два утверждения A и B, каждое из которых может быть истинным или ложным, т.е. принимать значения "1" или "0". Для этих двух утверждений всего существует 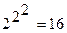различных логических операций, из которых содержательно интерпретируются лишь пять:

· дизъюнкция «ИЛИ» ;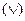

· конъюнкция «И» ();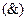

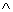· импликация «если - то» ;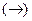

· эквивалентность «тогда и только тогда»;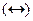

· сумма по модулю два или неоднозначность .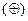

Таблицы истинности этих логических операций представлены в таблице 8.1.

Табл. 8.1.Таблицы истинности булевой логики

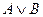
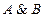
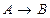
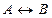
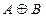
Предположим, что логическое утверждение может принимать не два значения истинности, а три, например: "истинно", "ложно" и "неопределенно". В этом случае мы будем иметь дело не с двухзначной, а трехзначной логикой. Общее количество бинарных операций, а, следовательно, и таблиц истинности, в трехзначной логике равно .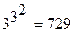

Нечеткая логика является разновидностью многозначной логики, в которой значения истинности задаются лингвистическими переменными или термами лингвистической переменной "истинность". Правила выполнения нечетких логических операций получают из булевых логических операций с помощью принципа обобщения.

Обозначим нечеткие логические переменные через 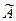и 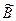, а функции принадлежности, задающие истинностные значения этих переменных через 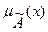и .

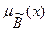Нечеткой логической конъюнкцией называется нечеткое высказывание с функцией принадлежности:

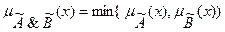(8.5)

Нечеткой логической дизъюнкцией называется нечеткое высказывание с функцией принадлежности:

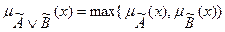(8.6)

Нечеткой логической импликацией называется нечеткое высказывание с функцией принадлежности:

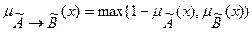(8.7)

Нечетким логическим отрицанием называется нечеткое высказывание с функцией принадлежности:

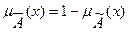(8.8)

В многозначной логике логические операции могут быть заданы таблицами истинности. В нечеткой логике количество возможных значений истинности может быть бесконечным, следовательно, в общем виде табличное представление логических операций невозможно. Однако, в табличной форме можно представить нечеткие логические операции для ограниченного количества истинностных значений, например, для терм-множества {«истинно», «очень истинно», «не истинно», «более-менее ложно», «ложно»}.

Для трехзначной логики с нечеткими значениями истинности «истинно» - 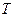; « ложно» - 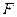и «неизвестно» - 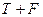Л. Заде предложил такие лингвистические таблицы истинности:

Табл. 8.2.Таблицы истинности трехзначной

нечеткой логики

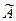
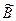
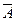
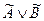
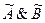
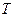
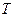
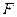
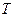
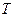
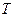
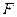
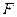
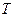
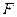
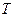
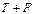
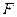
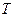
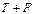
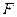
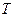
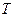
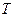
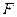
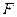
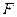
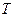
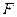
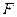
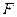
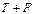
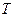
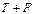
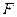
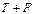
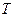
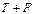
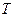
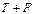
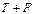
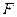
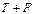
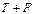
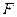
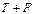
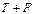
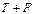
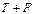
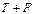
Применяя правила выполнения нечетких логических операций (8.5-8.8)з можно расширить таблицы истинности для большего количества термов. Как это сделать рассмотрим на следующем примере.

Пример 10. Заданы следующие нечеткие истинностные значения:

;

;

.

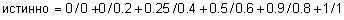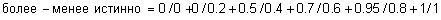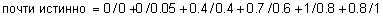Применяя правило из определения 45, найдем нечеткую истинность выражения "почти истинно ИЛИ истинно":

.

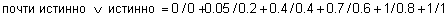Сравним полученное нечеткое множество с нечетким множеством "более-менее истинно". Они почти равны, значит:

.

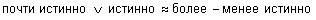В результате выполнения логических операций часто получается нечеткое множество, которое не эквивалентно ни одному из ранее введенных нечетких значений истинности. В этом случае необходимо среди нечетких значений истинности найти такое, которое соответствует результату выполнения нечеткой логической операции в максимальной степени. Другими словами, необходимо провести так называемую лингвистическую аппроксимацию, которая может рассматриваться как аналог аппроксимации эмпирического статистическими распределения стандартными функциями распределения случайных величин. В качестве примера приведем предложенные Балдвином лингвистические таблицы истинности для показанных на рис. 15 нечетких значений истинности:

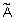
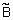
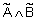
ложно	ложно	ложно	ложно
истинно	ложно	ложно	истинно
истинно	истинно	истинно	истинно
неопределенно	ложно	ложно	неопределенно
неопределенно	истинно	неопределенно	истинно
неопределенно	неопределенно	неопределенно	неопределенно
истинно	очень истинно	истинно	очень истинно
истинно	более-менее истинно	более-менее истинно	истинно

9. ЛИТЕРАТУРА

1. Н. Нефедова, В. А. Осипов Курс дискретной математики. 1992

2. С. В. Яблонский Введение в дискретную математику. 1979

3. О. П. Кузнецов, Г. М. Адельсон-Вельский Дискретная математика для инженеров. 1980

4. Л. М. Лихтарников, Т. Г. Сукачева Математическая логика. 1998

5. В. Г. Карпов, В. А. Мощенский Математическая логика и дискретная математика. 1977

6. И. Б. Сироджа. Примеры и задачи комбинаторики и теории графов. 1986

7. О. Оре Теория графов. 1980

8. А. Е. Соловьев, В. С. Галкин Основы дискретной математики.

9. Ф. А. Новиков Дискретная математика для программистов.

Дата добавления: 2013-12-12