Концентрации электролита

Рис.5.6. Зависимость скорости коагуляции от

В области медленной коагуляции скорость сильно зависит от концентрации (отрезок АВ). В точке В скорость становиться постоянной и не зависит от концентрации электролита – здесь значение z - потенциала равно нулю – начало быстрой коагуляции. Концентрацию электролита, начиная с которой скорость коагуляции остается постоянной, называют порогом быстрой коагуляции.

Теории кинетики коагуляции разработаны Смолуховским (1916г).

Рассматривают коагуляцию как реакцию второго порядка, в элементарном акте которой участвуют две частицы: .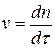

Уравнение Смолуховского для расчета числа частиц, слипшихся по m-штук за время t:

;

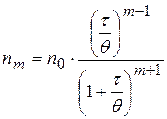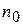- первоначальное число частиц;

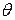- время половинной коагуляции ().

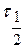При быстрой коагуляции все столкнувшиеся частицы реагируют (DU_б=0).

Уравнение Смолуховского для константы скорости быстрой коагуляции:

;

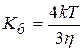где h- вязкость среды.

При медленной коагуляции не все столкновения приводят к слипанию. Уравнение Смолуховского для медленной коагуляции:

;

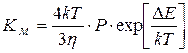где Р – стерический множитель, учитывающий благоприятные пространственные расположения частиц при столкновении, их физические размеры. При быстрой коагуляции все столкновения эффективны и Р=1, при медленной Р<1.

DЕ – потенциальный барьер, при быстрой коагуляции DЕ=0, при медленной DЕ¹0.

h - вязкость.

Порог коагуляции можно вычислить из соотношения, теоретически найденного Дерягиным и Ландау и названным законом 6-й степени:

энергетический барьер между коллоидными частицами исчезает при достижении критической концентрации (g), которая обратно пропорциональна шестой степени заряда иона-коагулятора:

;

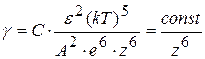С – константа, зависящая от числа зарядов катиона и аниона;

e - диэлектрическая проницаемость раствора;

А – константа Ван –дер –Ваальсового притяжения;

е- заряд электрона;

k – константа Больцмана;

z– зарядность коагулирующего иона.

В соответствии с этим уравнением значения g для элементов с зарядами противоионов 1, 2 и 3 соотносятся как 1:1/2⁶:1/3⁶=1:1/64:1/729.

Уравнение хорошо обосновывает эмпирическое правило Шульце-Гарди.

В тех случаях, когда велика роль адсорбционно-сольватного фактора устойчивости, проявляется приближенность теории ДЛФО, т.к. она не учитывает роли специфической адсорбции и сродства иона к растворителю.

Связь эффективности соударений с потенциальным барьером при коагуляции была показана Фуксом Н.А.

Если DЕ значительно больше кТ, то скорость коагуляции может приблизиться к нулю и система окажется агрегативно неустойчивой.

В теории, развитой Фуксом, используется представление о коэффициенте замедления коагуляции W, который показывает, во сколько раз константа скорости медленной коагуляции меньше константы скорости быстрой коагуляции. Учитывая выражения для К_б и К_м, получим:

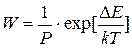
Коэффициент W называют фактором устойчивости или коэффициентом стабильности.

Дата добавления: 2013-12-12