Принятие решений в условиях риска

Обзор и классификация

Аналитические методы

Методы формального представления систем

В МПФС можно выделить:

1) аналитические методы;

2) статистические методы;

3) теоретико-множественные методы;

4) логические методы;

5) лингвистические и семиотические методы;

6) графические методы и пр.

Названные методы могут использоваться в различных комбинациях, а также в сочетании с МАИС.

К аналитическим относится большинство методов исследования операций.

Исследование операций в широком смысле слова представляет собой математический аппарат поддержки процесса принятия решений в различных областях человеческой деятельности. При этом операцией называют любое управляемое мероприятие, объединенное общим замыслом и направленное на достижение определенной цели.

Для моделирования операций используются оптимизационные модели. В большинстве из них используется аппарат математического программирования: максимизируется или минимизируется целевая функция при заданных ограничениях. Задача математического программирования уже рассматривалась при изучении принципа оптимальности. Есливсе функции в модели – линейные, то это задача линейного программирования (примеры изучались на практических занятиях). В общем случае эти функции могут быть любыми, т.е. могут строиться и задачи нелинейного программирования. Те и другие задачи могут быть целочисленными (когда переменные принимают только целые значения) либо непрерывными (например, задача о самолетах, изученная на практических занятиях, представляет собой пример целочисленной линейной задачи, а задача о кондитерской фабрике – непрерывной, поскольку объем выпуска конфет может измеряться и дробным числом). Целочисленность может быть полной либо частичной (относиться ко всем или не ко всем переменным модели). Если параметры модели (числовые данные, характеризующие экономическую ситуацию) представляют собой не константы, а в свою очередь зависят от некоторого параметра (например, от времени), то такая задача будет параметрической (на практических занятиях изучались упрощенные примеры, когда одна из констант полностью заменяется параметром (а не функцией от параметра)).

Каждый из этих типов моделей в свою очередь может быть подразделен на большое количество классов. Например, в линейном программировании можно выделить задачи производственного планирования (например, задача о кондитерской фабрике), транспортные задачи и т.д.

Для различных классов задач разработаны специальные методы решения. Студенты уже имеют опыт применения наиболее простых из подобных методов – графических способов решения. Однако, если переменных в модели более 2-3, ее уже невозможно решить упрощенно. Для решения таких задач используется более сложный математический аппарат: симплекс-метод для линейных моделей и различные модификации градиентных методов – для нелинейных. В рамках данной дисциплины не ставится задача подробного изучения этих методов. Программные средства, реализующие решение таких задач названными методами, являются доступными и широко известными. Например, программа Excel, входящая в стандартный пакет MSOffice, включает в себя надстройку «Поиск решения», предназначенную для решения задач математического программирования.

Особым видом оптимизационных моделей являются модели динамического программирования, с помощью которых исследуют многоэтапные операции. При этом, если эффективность всей операции складывается из критериев эффективности каждого этапа, то строится модель с аддитивным критерием, а если отдельные критерии перемножаются, то с мультипликативным критерием.

Особый вид оптимизационных моделей представляют собой также модели теории игр* (математические модели конфликтных ситуаций). Стороны в конфликте называют игроками. Здесь также существует большое разнообразие моделей - игры могут быть:

- коалиционные или бескоалиционные (в зависимости от того, позволяют ли правила сторонам согласовывать свои действия),

- конечные и бесконечные (в зависимости от того, имеется ли хотя бы у одной стороны бесконечное число стратегий, т.е. вариантов действий),

- с нулевой или ненулевой суммой (в играх с нулевой суммой общая величина проигрыша равняется величине выигрыша, т.е. сумма платежей равна нулю); и т.д.

Особый класс моделей теории игр составляют игры с природой. В таких играх одна из сторон (экономическая среда) не является сознательным противником, но создает проблему неопределенностью своих действий.

Рассмотрим методы решения таких моделей более подробно.

Как уже было сказано, речь пойдет о моделировании стохастических систем, т.е. необходимо будет учесть элемент неопределенности.

Условия неопределенности при принятии решений принято делить на:

а) условия риска (когда известны вероятности поведения природы);

б) условия «дурной неопределенности» (когда даже эти вероятности неизвестны).

Здесь используются различные средства теории вероятностей. Например, можно подсчитать математическое ожидание выигрыша – его среднее значение при неограниченно большом числе опытов. Рассчитав его при различных стратегиях, в качестве оптимальной выбирают ту из них, для которой оно является наибольшим.

Например, предприятие может выпускать один из трех видов продукции. Матрица 3 х 4 характеризует прибыль фирмы от выпуска i–го вида продукции (А_i) при j–м состоянии спроса (П_j); ее элементы обозначим a_ij, 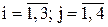. Известны вероятности каждого состояния спроса p_j. Их сумма равна единице, так как одно и только одно из них обязательно будет иметь место. Математическое ожидание выигрыша (прибыли) a_i при выпуске i–го вида продукции подсчитаем, как среднее взвешенное значений прибыли, используя в качестве весов вероятности состояний спроса (например, а₁ = 1*0.1 + 4*0.2 + 5*0.5 + 9*0.2 = 5.2):

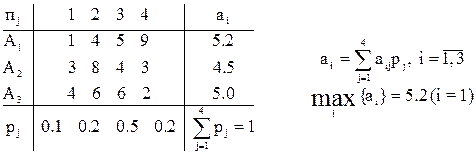
Следовательно, А₁ – оптимальная стратегия, ожидаемая прибыль равна 5.2 ден.ед.

Подчеркнем, что принятое решение является оптимальным не в каждом отдельном случае, а в среднем, при МНОГОКРАТНОМ повторении ситуации.

Например, если речь идет о дневной прибыли, то выпуская первый вид продукции в течении одного дня, фирма, возможно, получит и меньшую прибыль, чем получила бы, выпуская другой вид продукции. Прибыль будет оптимальной (максимальной), если просуммировать ее за 100 или 1000 дней, потому что только при большом количестве опытов вступают в действие законы теории вероятностей, но даже в этом случае величина прибыли не будет гарантированной.

Многократном повторение опыта не обязательно должно быть во времени, но может иметь место и в пространстве. Т.е. если прибыль задана для одного филиала фирмы, то речь может идти о применении оптимальной стратегии, например, сотней таких однотипных филиалов.

Другой метод основан на понятии риска.

Риск – это разность между выигрышем игрока, который он получил бы, если бы знал ситуацию среды (и соответственно выбрал бы стратегию) и выигрышем, который он получит в тех же условиях, используя стратегию A_i: r_ij=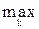{a_kj} - a_ij.

Из определения всегда r_ij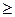0.

Составим матрицу рисков для предыдущего примера. Для этого вначале в каждом столбце матрицы найдем наибольший элемент (если бы состояние спроса было заранее известно, то была бы выбрана именно эта стратегия). Чтобы подсчитать риск, каждый элемент столбца вычтем из этой величины. Например, при первом состоянии спроса наибольшая прибыль достигается при выпуске третьего вида продукции, и равна 4. Если использовать первую стратегию, то прибыль будет равна 1. Следовательно, риск r₁₁=4-1=3. Аналогично r₂₁=4-3=1; r₃₁=4-4=0. При втором состоянии спроса наибольшая прибыль – 8 - может быть получена при выпуске второго вида продукции, поэтому все элементы второго столбца вычитаются из 8, и т.д.

Найдем с помощью матрицы рисков оптимальную стратегию (для которой ожидаемый риск r_i – наименьший).

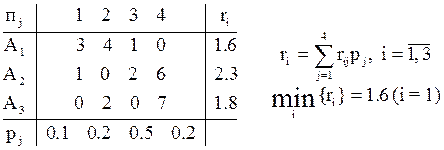
Следовательно, А₁ – оптимальная стратегия; т.е. результат совпал с предыдущим.

ЛЕКЦИЯ 15

Можно показать, что решения, найденные этими двумя способами, всегда будут совпадать*.

Дата добавления: 2013-12-12