
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция № 4. Уравнения прямой на плоскости. Взаимное расположение двух прямых на плоскости. Условия параллельности и перпендикулярности двух прямых. Расстояние от точки до прямой
|
|
|
|
Лекция № 3. Понятие об мерном векторном пространстве. Линейная зависимость и независимость векторов. Базис. Координаты вектора. Операции над векторами в координатах.
Лекция № 2. Декартова система координат на плоскости. Операции над векторами в координатах. Угол между двумя векторами. Скалярное произведение векторов и его свойства. Вычисление скалярного произведения, если известны координаты векторов.
Лекция № 1. Понятие вектора. Векторы на прямой. Линейные операции над векторами на прямой: сложение векторов, умножение вектора на число. Декартова система координат на прямой. Простейшие задачи аналитической геометрии. Векторы на плоскости. Коллинеарные и неколлиниарные векторы. Равенство векторов. Линейные операции над векторами на плоскости.
Направленный отрезок с начальной точкой 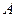 и конечной точкой
и конечной точкой 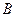 будем называть вектором и обозначать символом
будем называть вектором и обозначать символом 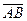 . Точку
. Точку 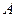 часто называют точкой приложения вектора
часто называют точкой приложения вектора 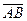 , числовой характеристикой вектора
, числовой характеристикой вектора 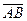 является длина отрезка
является длина отрезка 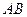 , а направление указывают стрелкой.
, а направление указывают стрелкой.
Длину отрезка 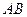 называют также модулем вектора и обозначают
называют также модулем вектора и обозначают 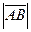 . В тех случаях, когда начальная и конечная точки вектора не важны, используют более простое обозначение вектора:
. В тех случаях, когда начальная и конечная точки вектора не важны, используют более простое обозначение вектора:  .
.
Вектор, у которого начальная и конечная точки совпадают, называют нулевым вектором и обозначают символом 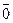 . Легко видеть, что длина нулевого вектора равна 0, а направление не определено. Условились направление нулевого вектора выбирать произвольно в зависимости от условий задачи.
. Легко видеть, что длина нулевого вектора равна 0, а направление не определено. Условились направление нулевого вектора выбирать произвольно в зависимости от условий задачи.
Рассмотрим сначала множество векторов, лежащих на некоторой прямой  . Легко видеть, что любые два вектора на прямой
. Легко видеть, что любые два вектора на прямой  могут иметь либо одинаковое направление (в этом случае их называют сонаправленными), либо противоположные направления (в этом случае их называют противоположно направленными). Два вектора
могут иметь либо одинаковое направление (в этом случае их называют сонаправленными), либо противоположные направления (в этом случае их называют противоположно направленными). Два вектора  и
и  на прямой
на прямой  назовем равными (обозначение
назовем равными (обозначение 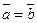 ), если при совмещении их начальных точек совпадут их конечные точки. Ясно, что это произойдет тогда и только тогда, когда
), если при совмещении их начальных точек совпадут их конечные точки. Ясно, что это произойдет тогда и только тогда, когда  и
и  имеют одинаковое направление и одинаковую длину. Все нулевые векторы считаются равными.
имеют одинаковое направление и одинаковую длину. Все нулевые векторы считаются равными.
Рассмотрим теперь линейные операции над векторами на прямой  : сложение векторов и умножение вектора на число.
: сложение векторов и умножение вектора на число.
Определение 1. Суммой двух векторов  и
и  на прямой
на прямой  назовем
назовем
вектор 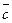 , начало которого совпадает с началом
, начало которого совпадает с началом
вектора  , а конец – с концом вектора
, а конец – с концом вектора  , при
, при
условии, что вектор  приложен к концу вектора
приложен к концу вектора  .
.
Обозначение: 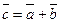 . Из определения 1 ясно, вектор
. Из определения 1 ясно, вектор 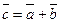 лежит на прямой
лежит на прямой  , направление его совпадает с направлением большего по длине вектора
, направление его совпадает с направлением большего по длине вектора  или
или  , а длина равна сумме длин векторов
, а длина равна сумме длин векторов  и
и  , если они сонаправлены и модулю разности длин векторов
, если они сонаправлены и модулю разности длин векторов  и
и  , если они противоположно направлены.
, если они противоположно направлены.
Если векторы  и
и  имеют противоположные направления и равны по длине, то
имеют противоположные направления и равны по длине, то 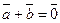 . В этом случае вектор
. В этом случае вектор  называют противоположным для вектора
называют противоположным для вектора  и обозначают
и обозначают 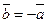 . Операцию сложения двух векторов на прямой
. Операцию сложения двух векторов на прямой  можно распространить на любое число слагаемых векторов.
можно распространить на любое число слагаемых векторов.
Операция сложения векторов на прямой  обладает следующими свойствами:
обладает следующими свойствами:
· 1). 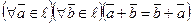 (коммутативный закон).
(коммутативный закон).
· 2). 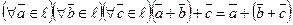 (ассоциативный закон).
(ассоциативный закон).
Определение 2. Произведением вектора  на прямой
на прямой  на число
на число 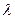
называется вектор, обозначаемый 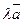 , на прямой
, на прямой  ,
,
удовлетворяющий условиям:
1) 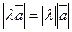 ;
;
2) векторы  и
и 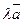 сонаправлены, если
сонаправлены, если 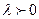 и противоположно направлены, если
и противоположно направлены, если 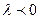 .
.
Очевидно, что при 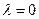 вектор
вектор 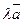 является нулевым вектором.
является нулевым вектором.
Операция умножения вектора на число на прямой  обладает свойствами
обладает свойствами
· 3) 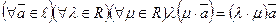 (ассоциативный закон).
(ассоциативный закон).
· 4) 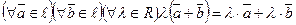 (дистрибутивный закон относительно суммы векторов).
(дистрибутивный закон относительно суммы векторов).
· 5) 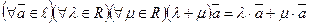 (дистрибутивный закон относительно суммы чисел).
(дистрибутивный закон относительно суммы чисел).
Заметим, что разность векторов 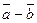 можно рассматривать как сумму векторов
можно рассматривать как сумму векторов  и
и 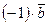 .
.
Зададим на прямой  положительное направление (стрелкой), выберем некоторую точку
положительное направление (стрелкой), выберем некоторую точку 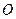 , которую назовем началом отсчета, и укажем единицу измерения – некоторый вектор
, которую назовем началом отсчета, и укажем единицу измерения – некоторый вектор 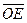 , сонаправленный с положительным направлением прямой
, сонаправленный с положительным направлением прямой  . Вектор
. Вектор 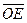 называют единичным вектором.
называют единичным вектором.
Прямую  с заданным положительным направлением, выбранным началом отсчета
с заданным положительным направлением, выбранным началом отсчета 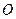 и единичным вектором называют осью, или системой координат на прямой. При этом точку О называют началом координат, а единичный вектор
и единичным вектором называют осью, или системой координат на прямой. При этом точку О называют началом координат, а единичный вектор 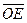 обозначают символом
обозначают символом 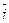 . Выберем на прямой
. Выберем на прямой  произвольно точку
произвольно точку 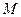 и рассмотрим вектор
и рассмотрим вектор 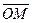 как произведение вектора
как произведение вектора 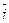 на некоторое действительное число
на некоторое действительное число 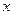 :
: 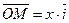 . Ясно, что такое число
. Ясно, что такое число 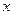 будет единственным и оно равно длине вектора
будет единственным и оно равно длине вектора 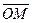 , взятой со знаком «+», если вектор
, взятой со знаком «+», если вектор 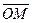 сонаправлен с вектором
сонаправлен с вектором 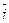 и со знаком «-», если вектор
и со знаком «-», если вектор 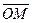 противоположно направлен относительно
противоположно направлен относительно 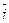 . Такое число
. Такое число 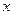 называют координатой точки М и обозначают символом
называют координатой точки М и обозначают символом 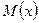 .
.
Зная координаты двух точек 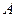 и
и 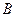 прямой
прямой  , можно найти расстояние между этими точками, а также вычислить координату точки, делящей вектор
, можно найти расстояние между этими точками, а также вычислить координату точки, делящей вектор 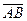 в заданном отношении. Эти две задачи называют простейшими задачами аналитической геометрии.
в заданном отношении. Эти две задачи называют простейшими задачами аналитической геометрии.
Расстояние между 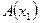 и
и 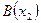 равно
равно 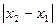 .
.
Определение 3. Будем говорить, что точка М, лежащая между 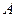 и
и 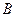 ,
,
делит вектор 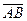 в отношении
в отношении 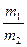 , если
, если 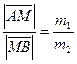 .
.
Здесь 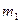 и
и 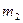 - произвольные положительные действительные числа. Зная
- произвольные положительные действительные числа. Зная 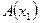 и
и 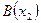 , выведем формулу, по которой вычисляется координата точки М, делящей вектор
, выведем формулу, по которой вычисляется координата точки М, делящей вектор 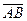 в отношении
в отношении 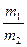 . Обозначим через
. Обозначим через 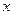 координату точки М, Тогда
координату точки М, Тогда 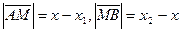 . По условию
. По условию 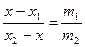 . Отсюда получаем
. Отсюда получаем 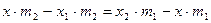 , или
, или 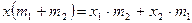 , или
, или 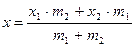 . В частности, если
. В частности, если 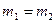 (т.е. М – середина вектора
(т.е. М – середина вектора 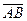 ), то получаем
), то получаем 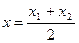 .
.
Рассмотрим теперь множество векторов, лежащих на некоторой плоскости. Если на прямой любые два вектора сонаправлены или противоположно направлены, то на плоскости они могут иметь различные направления.
Определение 4. Два вектора на плоскости, лежащие на одной прямой
или на параллельных прямых, называют
коллинеарными, в противном случае –
неколлинеарными.
Легко видеть, что коллинеарные векторы (как и векторы на прямой) либо сонаправлены, либо противоположно направлены.
Определение 5. Два вектора  и
и  на плоскости называют равными,
на плоскости называют равными,
если они коллинеарны, сонаправлены и имеют
одинаковую длину. В этом случае пишут 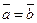 . Если
. Если
же векторы имеют одинаковую длину, коллинеарны
и противоположно направлены, их называют
противоположными.
Определение 6. Суммой двух векторов  и
и  назовем вектор
назовем вектор 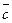 ,
,
начало которого совпадает с началом вектора  , а
, а
конец – с концом вектора  , при условии, что вектор
, при условии, что вектор
 приложен к концу вектора
приложен к концу вектора  .
.
Такое правило сложения двух векторов на плоскости называют правилом треугольника (если векторы  и
и  неколлинеарны, то вместе с вектором
неколлинеарны, то вместе с вектором 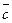 они образуют треугольник).
они образуют треугольник).
Существует другой способ сложения неколлинеарных векторов  и
и  на плоскости. Можно вектор
на плоскости. Можно вектор  приложить к началу вектора
приложить к началу вектора  и построить параллелограмм на векторах
и построить параллелограмм на векторах  и
и  . Тогда вектор, совпадающий по длине с диагональю этого параллелограмма, выходящей из общей точки приложения векторов
. Тогда вектор, совпадающий по длине с диагональю этого параллелограмма, выходящей из общей точки приложения векторов  и
и  , будет суммой
, будет суммой 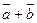 . Это правило сложения векторов называют правилом параллелограмма.
. Это правило сложения векторов называют правилом параллелограмма.
Операцию сложения двух векторов на плоскости так же как и на прямой можно распространить на любое число слагаемых векторов. При этом операция сложения векторов будет удовлетворять свойствам 1) – 2).
Определение 7. Произведением вектора  на число
на число 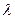 называется
называется
вектор, обозначаемый 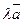 , удовлетворяющий
, удовлетворяющий
условиям:
1) 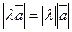 ;
;
2) вектор 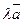 коллинеарен вектору
коллинеарен вектору  ;
;
3) векторы  и
и 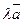 сонаправлены, если
сонаправлены, если 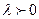 и противоположно направлены, если
и противоположно направлены, если 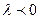 .
.
Очевидно, что при 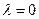 вектор
вектор 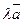 является нулевым вектором.
является нулевым вектором.
Операция умножения вектора на число удовлетворяет ассоциативному закону: 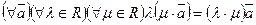 ; дистрибутивному закону относительно суммы векторов:
; дистрибутивному закону относительно суммы векторов: 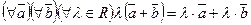 и дистрибутивному закону относительно суммы чисел:
и дистрибутивному закону относительно суммы чисел: 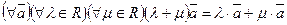 .
.
Теорема 1. Чтобы два ненулевых вектора  и
и  были коллинеарны,
были коллинеарны,
необходимо и достаточно существование числа 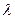 такого,
такого,
что 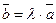 .
.
Рассмотрим на плоскости две оси 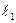 и
и 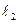 , пересекающиеся в точке
, пересекающиеся в точке 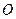 , которая является началом отсчета на каждой из осей. Совокупность таких осей определяет афинную систему координат на плоскости. При этом точку
, которая является началом отсчета на каждой из осей. Совокупность таких осей определяет афинную систему координат на плоскости. При этом точку 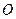 называют началом системы координат, а оси
называют началом системы координат, а оси 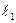 и
и 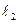 – осями координат. Если угол между осями координат равен 90° (прямой), то систему координат называют прямоугольной. Если единичные векторы на осях координат имеют одинаковую длину, то систему координат называют декартовой в честь Р.Декарта, который впервые начал рассматривать такие системы координат. В школьном курсе математики используется лишь прямоугольная декартова система координат. В нашем курсе мы также часто будем использовать прямоугольную (но не обязательно декартову) систему координат.
– осями координат. Если угол между осями координат равен 90° (прямой), то систему координат называют прямоугольной. Если единичные векторы на осях координат имеют одинаковую длину, то систему координат называют декартовой в честь Р.Декарта, который впервые начал рассматривать такие системы координат. В школьном курсе математики используется лишь прямоугольная декартова система координат. В нашем курсе мы также часто будем использовать прямоугольную (но не обязательно декартову) систему координат.
По традиции в прямоугольной системе координат на плоскости одну из осей (например 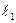 ) изображают горизонтально относительно наблюдателя, а другую – вертикально. Горизонтальную ось
) изображают горизонтально относительно наблюдателя, а другую – вертикально. Горизонтальную ось 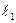 называют осью абсцисс и обозначают
называют осью абсцисс и обозначают 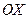 , а вертикальную ось
, а вертикальную ось 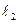 называют осью ординат и обозначают
называют осью ординат и обозначают 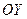 . Единичные векторы осей
. Единичные векторы осей 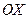 и
и 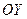 обозначают через
обозначают через 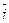 и
и 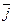 соответственно.
соответственно.
Пусть на плоскости задана прямоугольная декартова система координат. Возьмем произвольно точку 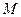 на этой плоскости и обозначим через
на этой плоскости и обозначим через 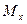 и
и 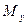 проекции точки
проекции точки 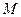 на оси
на оси 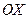 и
и 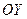 соответственно.
соответственно.
Допустим, что точка 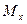 имеет координату
имеет координату 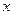 на оси
на оси 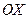 , а точка
, а точка 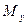 имеет координату
имеет координату 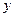 на оси
на оси 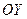 . Эти числа
. Эти числа 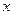 и
и 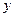 в указанном порядке называют декартовыми координатами точки
в указанном порядке называют декартовыми координатами точки 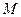 и этот факт обозначают символом
и этот факт обозначают символом 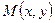 . При этом координату
. При этом координату 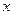 называют абсциссой точки
называют абсциссой точки 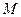 , а координату
, а координату 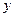 - ординатой точки
- ординатой точки 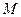 .
.
Легко видеть, что 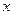 является проекцией вектора
является проекцией вектора 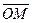 на ось абсцисс, а
на ось абсцисс, а 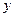 - проекцией вектора
- проекцией вектора 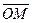 на ось ординат. Следовательно
на ось ординат. Следовательно 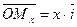 ,
, 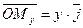 . Таким образом получаем
. Таким образом получаем
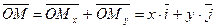 . (1)
. (1)
Упорядоченную пару чисел 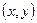 называют также координатами вектора
называют также координатами вектора 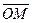 и этот факт обозначают символом
и этот факт обозначают символом 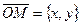 .
.
Поскольку точка 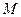 выбиралась произвольно, то равенство (1) означает, что любой вектор
выбиралась произвольно, то равенство (1) означает, что любой вектор 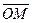 на плоскости можно выразить и притом единственным образом через единичные векторы координатных осей
на плоскости можно выразить и притом единственным образом через единичные векторы координатных осей 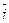 и
и 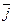 . Поэтому пару векторов
. Поэтому пару векторов 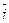 и
и 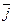 (в перечисленном порядке) называют базисом на плоскости, а равенство (1) разложением вектора
(в перечисленном порядке) называют базисом на плоскости, а равенство (1) разложением вектора 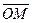 по базису. В частности
по базису. В частности 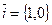 ;
; 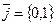 .
.
Пусть имеем две точки на плоскости 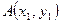 и
и 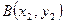 , заданные декартовыми координатами. Найдем расстояние между точками
, заданные декартовыми координатами. Найдем расстояние между точками 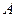 и
и 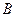 .
.
Длина вектора 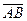 может быть найдена по теореме Пифагора из треугольника
может быть найдена по теореме Пифагора из треугольника  .
.
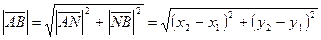 .
.
Рассмотрим теперь решение задачи о делении вектора 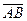 внутренней точкой
внутренней точкой 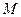 в отношении
в отношении 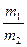 , если известно, что
, если известно, что 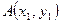 и
и 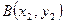 . Обозначим декартовы координаты точки
. Обозначим декартовы координаты точки 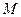 через
через 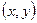 и пусть
и пусть 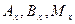 являются проекциями точек
являются проекциями точек 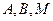 на оси
на оси 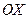 соответственно. Из подобия треугольников следует
соответственно. Из подобия треугольников следует 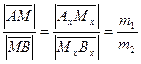 . Учитывая, что на оси
. Учитывая, что на оси 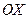
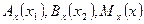 , получаем
, получаем 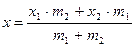 . Аналогично можно найти
. Аналогично можно найти 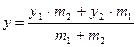 .
.
Рассмотрим теперь прямоугольную систему координат в трехмерном пространстве. Ее образуют три взаимно перпендикулярные оси 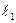 ,
, 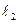 и
и 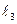 , пересекающиеся в точке
, пересекающиеся в точке 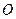 , которая является началом координат на каждой из осей. Если единичные векторы на каждой из осей имеют одинаковую длину, то систему координат называют декартовой.
, которая является началом координат на каждой из осей. Если единичные векторы на каждой из осей имеют одинаковую длину, то систему координат называют декартовой.
В ней оси 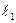 ,
, 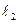 и
и 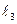 называют осью абсцисс (ось
называют осью абсцисс (ось 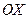 ), осью ординат (ось
), осью ординат (ось 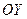 ) и осью апликат (ось
) и осью апликат (ось 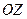 ) соответственно. Единичные векторы этих осей обозначают соответственно через
) соответственно. Единичные векторы этих осей обозначают соответственно через 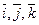 . Если в трехмерном пространстве произвольно взять точку
. Если в трехмерном пространстве произвольно взять точку 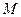 и найти ее проекции
и найти ее проекции 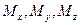 на оси
на оси 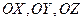 соответственно, то получим три числа
соответственно, то получим три числа 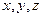 - координаты точек
- координаты точек 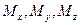 , которые в указанном порядке образуют декартовы координаты точки
, которые в указанном порядке образуют декартовы координаты точки 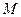 в трехмерном пространстве. Этот факт обозначают символом
в трехмерном пространстве. Этот факт обозначают символом 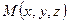 . Упорядоченная тройка чисел (
. Упорядоченная тройка чисел (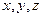 ), представляющая собой проекции вектора
), представляющая собой проекции вектора 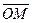 на оси координат, является также координатами вектора
на оси координат, является также координатами вектора 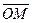 :
: 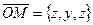 , а упорядоченная тройка векторов
, а упорядоченная тройка векторов 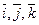 образует базис. Разложение вектора
образует базис. Разложение вектора 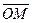 по этому базису имеет вид
по этому базису имеет вид 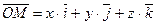 . В частности
. В частности 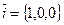 ;
; 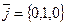 ;
; 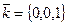 .
.
Решения простейших задач аналитической геометрии в трехмерном пространстве аналогичны решениям этих задач на плоскости.
Если имеем две точки 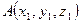 и
и 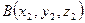 , заданные декартовыми координатами, то расстояние между ними вычисляется по формуле
, заданные декартовыми координатами, то расстояние между ними вычисляется по формуле
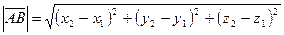 ,
,
а координаты точки 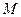 , делящей вектор
, делящей вектор 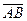 в отношении
в отношении 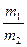 , находятся по формулам
, находятся по формулам 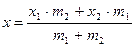 ,
, 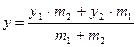 ,
, 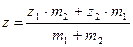 .
.
Пусть в трехмерном пространстве задана прямоугольная декартова система координат. Возьмем произвольно две точки 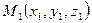 и
и 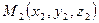 и поставим задачу: найти координаты вектора
и поставим задачу: найти координаты вектора 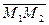 .
.
Соединив точки 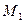 и
и 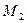 с началом координат
с началом координат 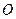 , получим
, получим 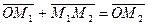 , или
, или 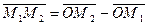 . Разлагая по базису каждый из векторов
. Разлагая по базису каждый из векторов 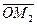 и
и 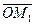 , будем иметь
, будем иметь
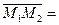
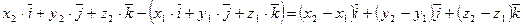 .
.
Это значит, что 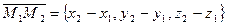 .
.
Выведем теперь формулы для нахождения координат суммы двух векторов и произведения вектора на число. Пусть имеем два вектора: 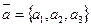 и
и 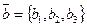 и число
и число 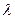 . Разложив данные векторы по базису, получим
. Разложив данные векторы по базису, получим 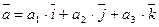 ,
, 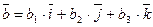 . Очевидно, что
. Очевидно, что 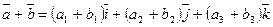 , или
, или 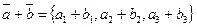 и
и 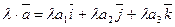 , или
, или 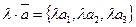 . Таким образом при сложении двух векторов их одноименные координаты складываются, а при умножении вектора на число каждая координата умножается на это число.
. Таким образом при сложении двух векторов их одноименные координаты складываются, а при умножении вектора на число каждая координата умножается на это число.
Два вектора, приложенные к общему началу, в плоскости этих векторов образуют между собой два угла 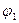 и
и 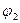 . Наименьший из этих углов назовем углом между векторами.
. Наименьший из этих углов назовем углом между векторами.
Определение 8. Скалярным произведением векторов  и
и  называют
называют
число, равное произведению длин этих векторов и
косинуса угла между ними.
Скалярное произведение векторов  и
и  будем обозначать символом
будем обозначать символом 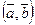 . По определению 8 имеем
. По определению 8 имеем 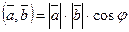 , где
, где 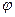 - угол между
- угол между  и
и  .
.
Теорема 2. Два вектора взаимно перпендикулярны тогда и только
тогда, когда их скалярное произведение равно нулю.
Справедливы следующие свойства скалярного произведения:
1°. 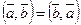 ;
;
2°. 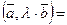
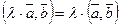 ;
;
3°. если векторы  и
и  взаимно перпендикулярны, то
взаимно перпендикулярны, то 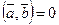 ;
;
4°. 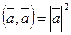 .
.
5°. 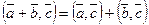 .
.
Теорема 3 Если векторы  и
и  заданы своими прямоугольными
заданы своими прямоугольными
декартовыми координатами 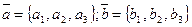 , то
, то
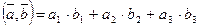 .
.
С помощью теоремы 3 можно находить длину вектора и косинус угла 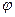 между двумя ненулевыми векторами, если известны декартовы координаты векторов. Действительно, считая что
между двумя ненулевыми векторами, если известны декартовы координаты векторов. Действительно, считая что 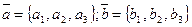 , получаем:
, получаем:
1) 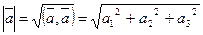 ;
;
2) 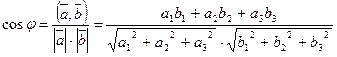 .
.
Любой вектор вполне определяется своими координатами: на прямой – некоторым действительным числом 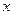 ; на плоскости – парой упорядоченных действительных чисел
; на плоскости – парой упорядоченных действительных чисел 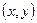 ; в трехмерном пространстве – тройкой упорядоченных действительных чисел
; в трехмерном пространстве – тройкой упорядоченных действительных чисел 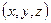 . Если отвлечься от геометрического образа вектора как направленного отрезка, то можно ввести в рассмотрение
. Если отвлечься от геометрического образа вектора как направленного отрезка, то можно ввести в рассмотрение 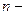 мерные векторы как упорядоченные наборы
мерные векторы как упорядоченные наборы 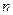 действительных чисел. По аналогии с трехмерным пространством числа, из которых состоят эти наборы, будем называть координатами
действительных чисел. По аналогии с трехмерным пространством числа, из которых состоят эти наборы, будем называть координатами 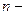 мерных векторов и обозначать
мерных векторов и обозначать 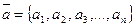 . В частности
. В частности 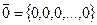 . Множество всех
. Множество всех 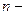 мерных векторов называют
мерных векторов называют 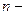 мерным векторным пространством и обозначают символом
мерным векторным пространством и обозначают символом 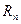 .
.
Два 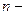 мерных вектора
мерных вектора 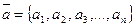 и
и 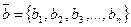 называют равными тогда и только тогда, когда
называют равными тогда и только тогда, когда 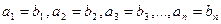 .
.
Суммой двух векторов 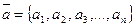 и
и 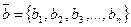 назовем вектор
назовем вектор 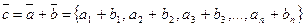 , а произведением вектора
, а произведением вектора 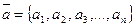 на число
на число 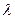 - вектор
- вектор 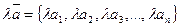 . Операция сложения векторов может быть распространена на любое число слагаемых векторов и удовлетворяет коммутативному и ассоциативному законам:
. Операция сложения векторов может быть распространена на любое число слагаемых векторов и удовлетворяет коммутативному и ассоциативному законам: 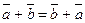 ;
; 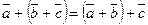 , а операция умножения вектора на число удовлетворяет ассоциативному закону:
, а операция умножения вектора на число удовлетворяет ассоциативному закону: 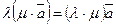 ; дистрибутивному закону относительно суммы векторов:
; дистрибутивному закону относительно суммы векторов: 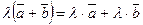 и дистрибутивному закону относительно суммы чисел:
и дистрибутивному закону относительно суммы чисел: 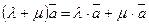 .
.
Скалярным произведением векторов 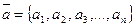 и
и 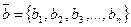 назовем число
назовем число 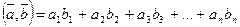 . Оно обладает такими же свойствами, что и на плоскости
. Оно обладает такими же свойствами, что и на плоскости
Определение 9. Векторы 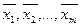 пространства
пространства 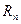 называют
называют
линейно зависимыми, если найдутся такие числа
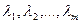 , одновременно не равные нулю, что
, одновременно не равные нулю, что
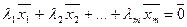 (*).
(*).
Если же равенство (*) выполняется только при
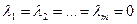 , то векторы
, то векторы 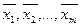 называют
называют
линейно независимыми.
Левую часть равенства (*) называют линейной комбинацией векторов 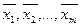 . На плоскости любые два коллинеарных вектора будут линейно зависимы, а любые два неколлинеарных вектора линейно независимы.
. На плоскости любые два коллинеарных вектора будут линейно зависимы, а любые два неколлинеарных вектора линейно независимы.
Любые три компланарных вектора (т.е. три вектора, лежащих в одной плоскости или в параллельных плоскостях) трехмерного пространства будут линейно зависимы, а любые три некомпланарных вектора – линейно независимы. В частности векторы 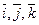 линейно независимы.
линейно независимы.
Свойства линейной зависимости векторов:
1°. Если среди векторов 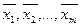 имеется нулевой вектор, то векторы
имеется нулевой вектор, то векторы 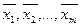 будут линейно зависимы.
будут линейно зависимы.
2°. Если среди векторов 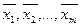 найдется хотя бы один, который можно представить в виде линейной комбинации остальных векторов, то векторы
найдется хотя бы один, который можно представить в виде линейной комбинации остальных векторов, то векторы 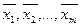 будут линейно зависимы.
будут линейно зависимы.
3°. Если среди векторов 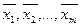 некоторые
некоторые 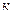 векторов
векторов 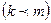 будут линейно зависимы, то векторы
будут линейно зависимы, то векторы 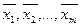 также будут линейно зависимы.
также будут линейно зависимы.
Определение 10. Будем говорить, что в пространстве 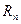 векторы
векторы
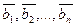 образуют базис, если они линейно
образуют базис, если они линейно
независимы и любой вектор 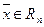 можно
можно
представить в виде их линейной комбинации:
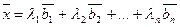 . При этом числа
. При этом числа 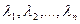
называют координатами вектора 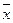 в базисе
в базисе
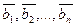 , а само равенство – разложением вектора
, а само равенство – разложением вектора 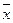
по базису 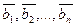 .
.
В частности, на прямой (в пространстве 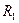 ) базис образует вектор
) базис образует вектор 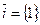 ; на плоскости (в пространстве
; на плоскости (в пространстве 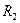 ) базис образуют векторы
) базис образуют векторы 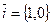 и
и 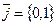 ; в трехмерном пространстве (в пространстве
; в трехмерном пространстве (в пространстве 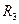 ) базисом являются векторы
) базисом являются векторы 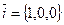 ,
, 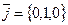 и
и 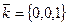 ; в пространстве
; в пространстве 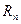 базис образуют
базис образуют 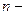 мерные векторы
мерные векторы 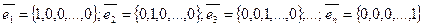 .
.
Пусть на плоскости задана прямоугольная декартова система координат. Выберем произвольно точку 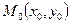 и зададим ненулевой вектор
и зададим ненулевой вектор 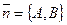 . Найдем уравнение прямой, проходящей через точку
. Найдем уравнение прямой, проходящей через точку 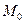 и перпендикулярной вектору
и перпендикулярной вектору 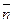 . Возьмем на искомой прямой произвольно точку
. Возьмем на искомой прямой произвольно точку 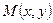 отличную от точки
отличную от точки 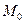 и рассмотрим вектор
и рассмотрим вектор 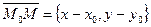 . Так как вектор
. Так как вектор 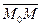 лежит на искомой прямой, которая должна быть перпендикулярна вектору
лежит на искомой прямой, которая должна быть перпендикулярна вектору 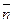 , то утверждаем, что векторы
, то утверждаем, что векторы 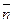 и
и 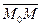 взаимно перпендикулярны. Значит по теореме 2 имеем
взаимно перпендикулярны. Значит по теореме 2 имеем 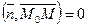 . Вычислив скалярное произведение по теореме 3, получаем
. Вычислив скалярное произведение по теореме 3, получаем 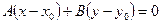 , или
, или 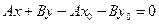 . Поскольку числа
. Поскольку числа 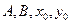 нам известны, то, обозначив число
нам известны, то, обозначив число 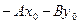 через
через 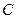 , получим уравнение
, получим уравнение
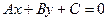 , (1)
, (1)
Так как точка 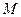 выбиралась на искомой прямой, а условие
выбиралась на искомой прямой, а условие 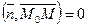 является необходимым и достаточным для перпендикулярности векторов
является необходимым и достаточным для перпендикулярности векторов 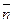 и
и 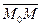 , то утверждаем, что полученное уравнение (1) и является уравнением искомой прямой. Его называют общим уравнением прямой, а вектор
, то утверждаем, что полученное уравнение (1) и является уравнением искомой прямой. Его называют общим уравнением прямой, а вектор 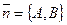 называют нормальным вектором для этой прямой. Учитывая, что этот вектор ненулевой, в уравнении (1) числа
называют нормальным вектором для этой прямой. Учитывая, что этот вектор ненулевой, в уравнении (1) числа 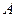 и
и 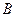 не могут одновременно равняться нулю.
не могут одновременно равняться нулю.
Рассмотрим теперь другие уравнения прямой на плоскости.
Возьмем уравнение (1) и для определенности положим, что 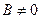 . Тогда поделив обе части уравнения (1) на
. Тогда поделив обе части уравнения (1) на 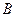 , получим
, получим 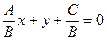 , или
, или 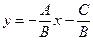 .
.
Обозначим 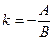 и
и 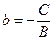 . Тогда уравнение (1) запишется в виде
. Тогда уравнение (1) запишется в виде
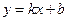 . (2)
. (2)
Число 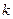 (равное тангенсу угла наклона прямой к положительному направлению оси
(равное тангенсу угла наклона прямой к положительному направлению оси 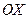 ) называют угловым коэффициентом прямой, а уравнение (2) – уравнением с угловым коэффициентом.
) называют угловым коэффициентом прямой, а уравнение (2) – уравнением с угловым коэффициентом.
Пусть теперь требуется найти уравнение прямой, если известен ее угловой коэффициент 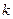 и одна точка
и одна точка 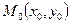 . Для решения такой задачи воспользуемся уравнением (2), в котором неизвестен параметр
. Для решения такой задачи воспользуемся уравнением (2), в котором неизвестен параметр 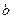 . Так как точка
. Так как точка 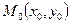 лежит на прямой, то ее координаты должны удовлетворять уравнению (2), т.е имеет место равенство
лежит на прямой, то ее координаты должны удовлетворять уравнению (2), т.е имеет место равенство 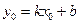 . Вычитая это уравнение из (2), получаем
. Вычитая это уравнение из (2), получаем
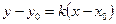 . (3)
. (3)
Уравнение (3) называют уравнением прямой с угловым коэффициентом и известной точкой.
Далее найдем уравнение прямой, проходящей через данную точку 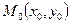 параллельно заданному ненулевому вектору
параллельно заданному ненулевому вектору 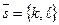 . Для этого возьмем на искомой прямой произвольно точку
. Для этого возьмем на искомой прямой произвольно точку 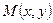 отличную от точки
отличную от точки 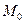 и рассмотрим вектор
и рассмотрим вектор 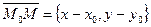 . Так как вектор
. Так как вектор 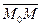 лежит на искомой прямой, которая должна быть параллельна вектору
лежит на искомой прямой, которая должна быть параллельна вектору 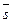 , то утверждаем, что векторы
, то утверждаем, что векторы 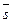 и
и 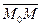 коллинеарны. Следовательно по теореме 1 найдется число
коллинеарны. Следовательно по теореме 1 найдется число 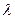 такое, что
такое, что 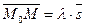 . Из равенства этих векторов следует равенство их одноименных координат:
. Из равенства этих векторов следует равенство их одноименных координат: 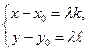 . Отсюда и получаем искомые уравнения прямой в виде
. Отсюда и получаем искомые уравнения прямой в виде
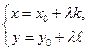 (4)
(4)
В уравнениях (4) число 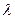 называют параметром, а сами уравнения – параметрическими.
называют параметром, а сами уравнения – параметрическими.
Если выразить параметр 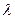 в каждом из уравнений (4) и приравнять, то получим уравнение прямой в виде
в каждом из уравнений (4) и приравнять, то получим уравнение прямой в виде
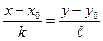 . (5)
. (5)
Уравнение (5) называют каноническим уравнением прямой.
Если некоторый вектор параллелен прямой, то его называют направляющим вектором этой прямой. Таким образом, в каноническом уравнении (5) в знаменателях дробей левой и правой частей стоят координаты направляющего вектора 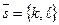 .
.
Если в общем уравнении прямой (1) выполняются условия 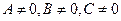 , то его называют полным. В противном случае уравнение (1) называют неполным. Допустим, что мы имеем полное уравнение (1). Перенесем число
, то его называют полным. В противном случае уравнение (1) называют неполным. Допустим, что мы имеем полное уравнение (1). Перенесем число 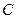 в правую часть и поделим обе части уравнения на
в правую часть и поделим обе части уравнения на 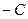 . Получим
. Получим 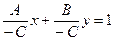 , или
, или 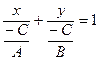 . Обозначив
. Обозначив 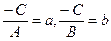 , приходим к уравнению
, приходим к уравнению
 , (6)
, (6)
которое называют уравнением прямой в отрезках. Если в уравнении (6) положить 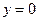 , то получим
, то получим 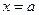 . Значит, точка
. Значит, точка 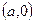 лежит на прямой и оси
лежит на прямой и оси 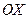 , отсекая, тем самым на этой оси отрезок длины
, отсекая, тем самым на этой оси отрезок длины 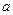 . Аналогично точка
. Аналогично точка 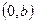 отсекает отрезок длины
отсекает отрезок длины 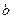 на оси
на оси 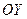 . Отсюда и название уравнения. Следует только иметь в виду, что если число
. Отсюда и название уравнения. Следует только иметь в виду, что если число 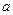 (или
(или 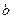 ) будет отрицательным, то отрезок длины
) будет отрицательным, то отрезок длины 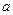 (или
(или 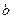 ) будет отсекаться на отрицательной полуоси.
) будет отсекаться на отрицательной полуоси.
И, наконец, найдем уравнение прямой, проходящей через две заданные точки 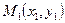 и
и  . Рассмотрим вектор
. Рассмотрим вектор 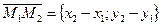 . Он является направляющим вектором искомой прямой. Поэтому для решения задачи воспользуемся каноническим уравнением (5), взяв в качестве известной точки, например, точку
. Он является направляющим вектором искомой прямой. Поэтому для решения задачи воспользуемся каноническим уравнением (5), взяв в качестве известной точки, например, точку 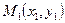 . Получим
. Получим
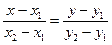 . (7)
. (7)
Заметим, что если бы мы в качестве известной точки взяли бы точку  , то получили бы уравнение в виде
, то получили бы уравнение в виде 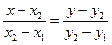 , которое легко приводится к уравнению (7), если к обеим частям прибавить число 1 и упростить.
, которое легко приводится к уравнению (7), если к обеим частям прибавить число 1 и упростить.
Пусть на плоскости имеем прямоугольную декартову систему координат, в которой заданы прямая  общим уравнением
общим уравнением 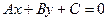 и точка
и точка 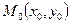 , не лежащая на
, не лежащая на  . Опустим из точки
. Опустим из точки 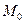 перпендикуляр на
перпендикуляр на  и обозначим основание этого перпендикуляра через
и обозначим основание этого перпендикуляра через 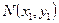 .
.
Из того, что точка 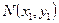 лежит на
лежит на  , имеем равенство
, имеем равенство 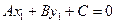 . Расстоянием от точки
. Расстоянием от точки 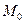 до прямой
до прямой  назовем длину перпендикуляра
назовем длину перпендикуляра 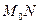 . Поставим задачу – найти расстояние от
. Поставим задачу – найти расстояние от 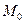 до
до  . Для этого рассмотрим два вектора: нормальный вектор
. Для этого рассмотрим два вектора: нормальный вектор 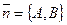 для прямой
для прямой  и
и 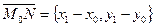 . Очевидно, что эти векторы коллинеарны. Следовательно, угол
. Очевидно, что эти векторы коллинеарны. Следовательно, угол 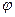 между ними равен либо
между ними равен либо 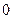 , либо
, либо 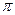 . Вычислим модуль скалярного произведения векторов
. Вычислим модуль скалярного произведения векторов 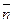 и
и 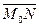 . С одной стороны,
. С одной стороны, 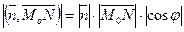 , а, с другой стороны,
, а, с другой стороны, 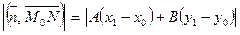 . Значит
. Значит 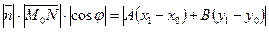 .
.
Заметив, что 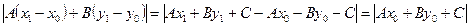 ,
,
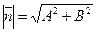 ,
,  , получаем равенство
, получаем равенство 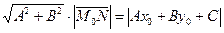 . Отсюда расстояние от
. Отсюда расстояние от 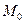 до
до  будет равно
будет равно 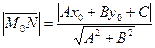 .
.
Легко видеть, что если точка 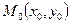 лежит на прямой
лежит на прямой  , то расстояние от
, то расстояние от 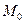 до
до  будет равно нулю, так как
будет равно нулю, так как 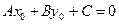 .
.
Рассмотрим теперь вопрос о взаимном расположении двух прямых 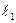 и
и 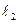 на плоскости. Если эти прямые пересекаются, то между ними образуется четыре угла с общей вершиной в точке пересечения. При этом различных углов будет только два. Очевидно, что если один из двух различных углов равен
на плоскости. Если эти прямые пересекаются, то между ними образуется четыре угла с общей вершиной в точке пересечения. При этом различных углов будет только два. Очевидно, что если один из двух различных углов равен 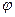 , то другой будет равен
, то другой будет равен 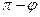 . Углом между прямыми
. Углом между прямыми 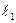 и
и 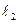 будем называть любой из углов
будем называть любой из углов 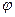 или
или 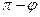 .
.
Допустим, что прямые 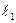 и
и 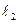 заданы общими уравнениями
заданы общими уравнениями 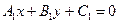 и
и 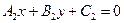 соответственно. Рассмотрим нормальные векторы
соответственно. Рассмотрим нормальные векторы 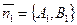 и
и 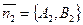 этих прямых. Легко заметить, что угол
этих прямых. Легко заметить, что угол 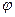 между
между