Системы линейных алгебраических уравнений

Матрицы. Операции над матрицами

Глава I. ЛИНЕЙНАЯ АЛГЕБРА

Определение 1. Прямоугольная таблица чисел 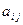вида

А = 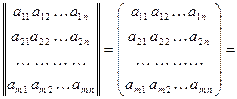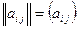, (1.1)

состоящая из m строк и n столбцов, называется матрицей размера 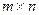. Числа 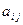называются ее элементами. Матрица размера 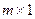называется матрицей-столбцом, размера 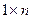- матрицей-строкой, размера 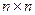- квадратной матрицей n-го порядка.

Таким образом, матрица-строка имеет вид 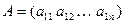, матрица-столбец 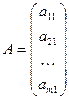, квадратная матрица n -го порядка 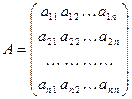. Элемент 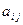находится на пересечении i -ой строки и j -го столбца матрицы.

Определение 2. Две матрицы 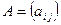и 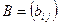называются равными, если они имеют одинаковые размеры 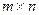и их соответствующие элементы равны: 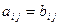. Пишут: А = В.

Определение 3. Матрица, все элементы которой равны нулю, называется нулевой матрицей. Единичной матрицей называется квадратная матрица вида 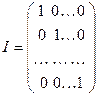, у которой 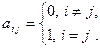Квадратная матрица вида 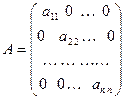называется диагональной матрицей (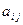=0, если 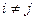), а матрица вида 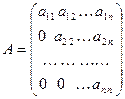- треугольной матрицей (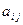= 0, если 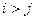). Прямоугольная матрица размера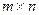 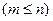называется ступенчатой, если она имеет вид А =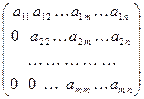 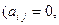если .

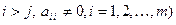Определение 4. Матрица 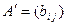называется транспонированной к матрице

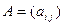, если она получена из матрицы А заменой ее столбцов строками с теми же

номерами, т.е. если .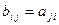

Таким образом, транспонированная к матрице А размера 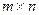матрица 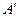имеет вид

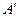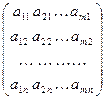= и размер .

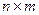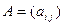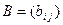Определение 5. Суммой (разностью)двух матриц и размера 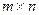называется матрица размера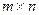 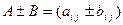, элементы которой равны сумме (разности) соответствующих элементов матриц А и В.

Определение 6. Произведением матрицы 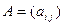на число 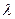называется матрица 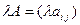, элементы которой равны произведению числа 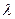на соответствующие элементы матрицы А.

Пример 1. Пусть 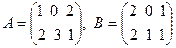. Найдем матрицу .

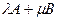Решение. По определениям 5 и 6 имеем .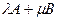

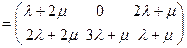Определение 7. Произведением матрицы 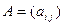размера 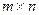на матрицу 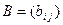размера 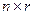называется матрица 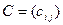размера 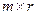, элементы которой вычисляются по формулам , .

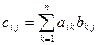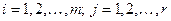Таким образом, элемент 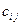матрицы 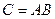есть сумма произведений элементов i -ой строки матрицы А на соответствующие элементы j -го столбца матрицы В. Поэтому для существования произведения АВ число столбцов матрицы А должно быть равно числу строк матрицы В. Ясно также, что из существования произведения АВ не следует существование произведения ВА.

Пример 2. Найдем произведение матрицы 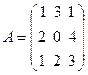на матрицу .

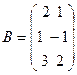Решение. Имеем .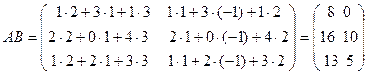

Свойства операций над матрицами:

А + В = В + А, А + (В + С) =(А + В) + С,

,

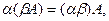
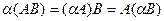А (ВС)=(АВ)С,

, ,

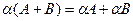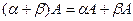А (В+С)= АВ + АС, (В + С) А = ВА + СА.

§ 2. Определители матриц

Определение 1. Определителем квадратной матрицы А = 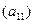1-го порядка (определителем 1-го порядка) называется число, обозначаемое 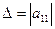и равное 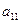. Определителем квадратной матрицы 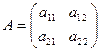2-го порядка (определителем 2-го порядка) называется число 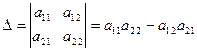. Определителем квадратной матрицы 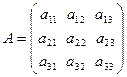3-го порядка (определителем 3-го порядка) называется число .

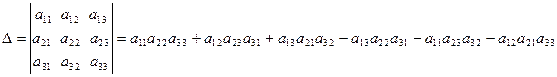При вычислении определителя 3-го порядка можно пользоваться правилом треугольника 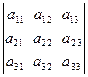. Отмеченные произведения берутся со знаком «+». Одна сторона треугольника здесь параллельна главной диагонали определителя .

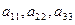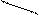
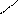
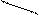
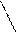
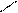
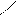
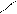
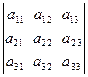- здесь указана побочная диагональ 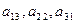и два треугольника, одна сторона которых параллельна этой диагонали. Соответствующие произведения берутся со знаком «».

Таким образом, определители 2-го и 3-го порядков являются алгебраическими суммами (т.е. суммами и разностями) всевозможных произведений элементов из каждой строки и каждого столбца определителя, причем из каждой строки и каждого столбца берется по одному элементу. Аналогичным образом можно ввести понятие определителя n -го порядка 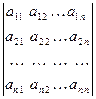. Вопрос только в том, как его вычислить, какие произведения элементов брать со знаком «+», а какие со знаком «». Ответ на этот вопрос дается с помощью понятия перестановки натуральных чисел, которое выходит за рамки нашей программы. Поэтому вычислять определители любого порядка мы научимся позднее с помощью разложения определителя по элементам его строки или столбца.

Определение 2.Величина 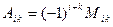, равная произведению определителя (n – 1)-го порядка 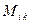, полученного из определителя n -го порядка вычеркиванием i -ой строки и k -го столбца, на число 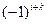, называется алгебраическим дополнением элемента .

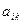Установим теперь свойства определителей.

Величина определителя:

а) не меняется, если у него заменить строки соответствующими столбцами.

Например,

.

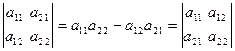б) меняет знак при перемене местами любых двух строк или любых двух столбцов. Например,

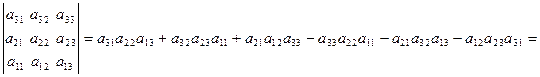
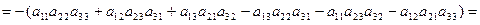
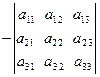
в) умножается на число k, если элементы какого-либо его столбца или строки умножить на k.

Например, .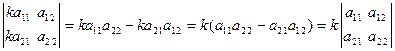

Из этого свойства следует, что общий множитель, присутствующий в строке или столбце, можно выносить за знак определителя.

г) равна нулю, если элементы какого-либо его столбца или строки равны нулю.

Например, .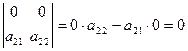

д) равна нулю, если элементы двух строк или столбцов соответственно равны. Например,

.

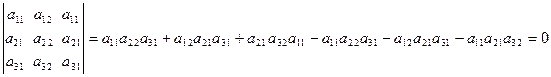е) Разложение Лапласа: сумма произведений элементов 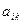некоторой строки или столбца определителя на алгебраические дополнения этих элементов равна величине определителя:

, .

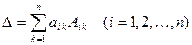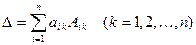Докажем это свойство для определителя третьего порядка в случае третьей строки. Имеем .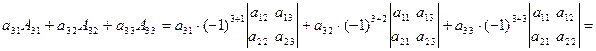

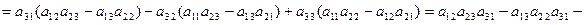
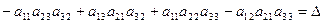Pierre Simon Laplace (1749-1827) – последний из ведущих математиков 18 века. Сын скромного землевладельца в Нормандии. Легко менял свои политические привязанности, что позволяло ему продолжать свою математическую деятельность при всех политических изменениях во Франции. Основные труды: «Аналитическая теория вероятностей» и «Небесная механика» в 5 томах.

Пример 1. .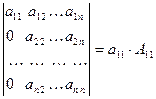

Пример 2. Если все элементы определителя 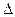, стоящие ниже (или выше) главной диагонали, равны нулю, то .

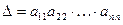Таким образом, определитель треугольной матрицы равен произведению элементов, стоящих на главной диагонали.

ж) Сумма произведений элементов 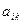некоторой строки (столбца) определителя на соответствующие алгебраические дополнения элементов другой строки (столбца) равна нулю: .

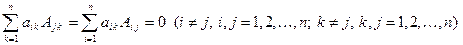Действительно, рассмотрим 1-ю сумму. Она не зависит от элементов j -ой строки (они вычеркнуты). Заменим в определителе элементы j -ой строки на соответствующие элементы i -ой строки. От этого рассматриваемая сумма не изменится. Между тем теперь ее можно рассматривать как разложение нового определителя по элементам j -ой строки, но тогда она равна величине нового определителя, который равен нулю на основании свойства д).

з) Пусть даны два определителя n -го порядка 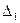и 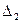, у которых все строки (столбцы) одинаковы, кроме одной строки (одного столбца). Сумма таких определителей равна определителю n -го порядка, у которого указанная строка (столбец) состоит из суммы соответствующих элементов этой строки (столбца) определителе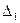й и .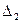

Например,

.

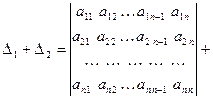
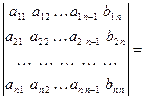
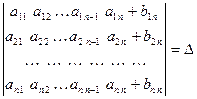Действительно, разлагая данные определители по элементам n -го столбца, получим .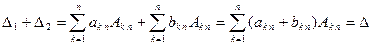

и) Величина определителя не изменится, если к элементам какой-либо его строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на число k.

(Иллюстрировать лучше на примере определителя 3-го порядка)

Например, 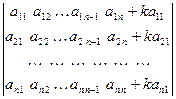= (см. свойства з) и в)) =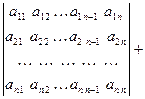 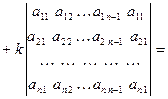(см. св - во д))==.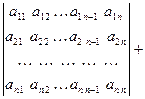

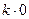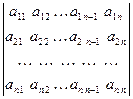С помощью последнего свойства вычисление данного определителя может быть сведено к вычислению определителя более низкого порядка или к вычислению определителя треугольной матрицы.

Пример 3. 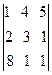= (к элементам 2-ой строки прибавим элементы 1-ой строки, умноженные на –2) = 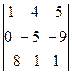= (к элементам 3-ой строки прибавим элементы 1-ой строки, умноженные на –8) = 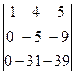= (см. пример 1) = 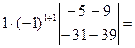(–5)(–39) – – (–9)(–31) = –84.

Пример 4. Вычислим определитель Вандермонда 4-го порядка 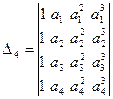(А.Т. Вандермонд (1735-1796) – французский математик).

Решение. Вычтем из элементов 2-ой, 3-ей и 4-ой строк соответствующие элементы 1-ой строки, получим 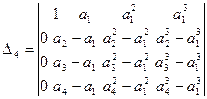. Вынесем за знак определителя общие множители 2-ой, 3-ей и 4-ой строк (свойство в)), затем вычтем из элементов 3-ей и 4-ой строк полученного определителя соответствующие элементы 2-ой строки: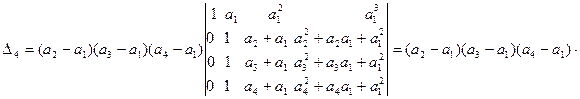 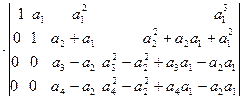. Вынесем за знак определителя общие множители 3-ей и 4-ой строк, затем вычтем из элементов 4-ой строки полученного определителя соответствующие элементы 3-ой строки:

.

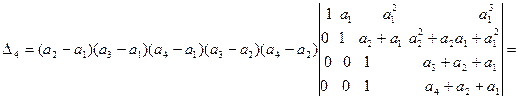
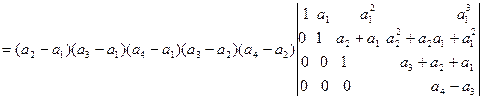Получился определитель треугольного вида, величина которого равна произведению элементов главной диагонали (см. пример 2), т.е. 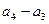. Поэтому .

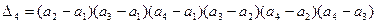Определение 1. Система уравнений вида

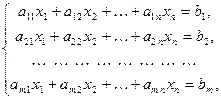(3.1)

где m и n - натуральные числа, 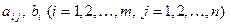- заданные числа, 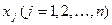- неизвестные, называется системой из m линейных алгебраических уравнений с n неизвестными (СЛАУ). Числа 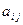называются коэффициентами при неизвестных, числа 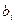- свободными членами.

Определение 2. Решением СЛАУ (3.1) называется такой набор чисел 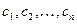, что каждое из уравнений системы обращается в тождество при подстановке 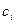вместо соответствующих неизвестных.

Определение 3. СЛАУ (3.1) называется совместной, если она имеет хотя бы одно решение, несовместной, если не имеет ни одного решения, определенной, если имеет единственное решение, неопределенной, если имеет более одного решения.

Определение 4. Две СЛАУ называются равносильными, если их решения совпадают.

Ясно, что если поменять местами какие-то уравнения системы (3.1), или умножить уравнение системы на число 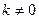, или прибавить к какому-то уравнению системы другое ее уравнение, умноженное на постоянное число, или исключить из системы уравнение, все коэффициенты которого равны нулю, то получим новую систему, равносильную данной. Поэтому указанным преобразованиям системы дали специальное название.

Определение 5. Перестановки уравнений системы (3.1), умножение какого-либо уравнения на число, отличное от нуля, прибавление к уравнению системы другого ее уравнения, умноженного на постоянное число, исключение из системы уравнения, все коэффициенты которого равны нулю, называются элементарными преобразованиями СЛАУ.

Определение 6. Каждой СЛАУ соответствует матрица, составленная из коэффициентов при неизвестных, которая называется матрицей системы. Матрица, полученная присоединением к матрице системы столбца свободных членов, называется расширенной матрицей системы.

Матрица системы (3.1) имеет вид

А = 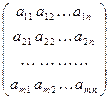, (3.2)

а ее расширенная матрица

В = 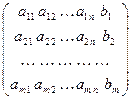. (3.3)

Очевидно, что преобразования СЛАУ приводят к аналогичным преобразованиям строк матрицы и расширенной матрицы системы. Поэтому имеет место

Определение 7. Перестановка строк матрицы, умножение какой-либо строки матрицы на число, отличное от нуля, прибавление к строке матрицы другой ее строки, умноженной на постоянное число, вычеркивание строки матрицы, все элементы которой равны нулю, называются элементарными преобразованиями матрицы. Если матрица В может быть получена из матрицы А с помощью элементарных преобразований, то матрицы А и В называются эквивалентными.

Если число уравнений системы (3.1) равно числу неизвестных, т.е. 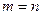, то имеет место

Теорема 1. Если определитель 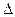матрицы системы (3.1) не равен нулю, то система (3.1) имеет единственное решение, вычисляемое по формулам Крамера

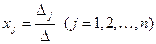, (3.4)

где 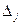- определитель матрицы, получаемой из матрицы А системы (3.1) заменой j -го столбца столбцом свободных членов.

Доказательство (не доказывал). Пусть 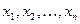- решение системы (3.1). Тогда все уравнения системы представляют собой тождества. Найдем 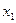. Для этого умножим 1-е уравнение системы на алгебраическое дополнение 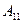, 2-е – на 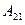,..., n -е – на 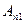и сложим все уравнения системы. Получим

.

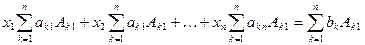По свойству е) 1-я сумма равна 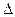, по свойству ж) остальные суммы в левой части равенства равны нулю, по свойству е) правая часть равна

.

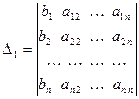Таким образом, имеем 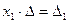. Поскольку 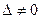по условию, .

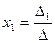Аналогичные рассуждения проводим в общем случае при определении 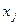. Первое уравнение умножаем на 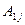, второе – на 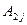,..., n -е – на 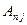, складываем полученные уравнения и на основании свойств е) и ж) определителей получаем

,

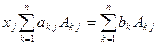т.е. 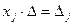, откуда .

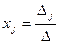Таким образом, мы доказали, что если 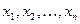- решение системы (3.1), то числа 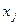определяются по формулам (3.4).

Обратно, покажем, что совокупность чисел 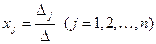, является решением системы (3.1). Действительно, подставляя 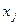(j = 1, 2, …, n) в левую часть k -го

уравнения системы (3.1), на основании свойств е) и ж) определителей, имеем

,

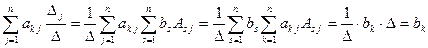т.е. числа (3.4) являются решением системы (3.1). Теорема доказана.

Г. Крамер (1704-1752) – швейцарский математик.

Пример 1. Решим систему уравнений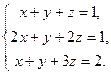

Решение. Имеем 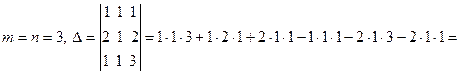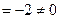. Поэтому решение системы можно найти по формулам Крамера (3.4). Поскольку 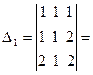2 + 4 + 1 – 2 – 2 – 2 = 1, 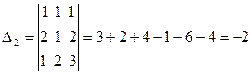, , 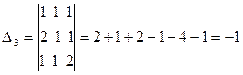получаем х = 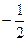, у = 1, 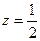. Ответ: .

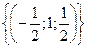Рассмотрим теперь частный случай системы (3.1), когда все .

Определение 8. Система уравнений вида

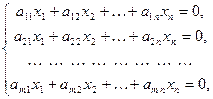(3.5)

называется однородной СЛАУ.

Очевидно, что числа 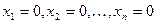являются решением однородной системы (3.5). Это решение называют тривиальным решением однородной системы (3.5). Нетривиальное решение однородной системы (3.5) – это решение, не являющееся тривиальным.

Теорема 2. Если определитель 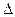матрицы однородной системы (3.5) не равен нулю, то эта система имеет только тривиальное решение.

Доказательство. В силу свойства г) определителя все 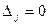. Поэтому по формулам (3.4) 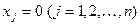. Теорема доказана.

Теорема 3. Если система уравнений (3.5) имеет нетривиальное решение, то определитель ее матрицы 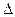необходимо равен нулю.

Доказательство. Предположим противное, т.е. что 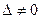. Тогда по теореме 2 система (3.5) имеет только тривиальное решение, что противоречит условию теоремы. Поэтому должно быть 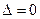. Ч.т.д.

Для исследования СЛАУ в общем случае, когда 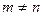, нам потребуется еще понятие ранга матрицы.

Определение 9. Рангом матрицы называется число, равное числу строк ступенчатой матрицы, эквивалентной данной матрице.

Ранг матрицы находится с помощью элементарных преобразований матрицы, распространенных также и на столбцы.

Пример 2. Найдем ранг матрицы .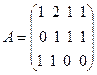

Решение. С помощью элементарных преобразований преобразуем матрицу А к ступенчатому виду. Прибавим к элементам 3-ей строки соответствующие элементы 1-ой строки, умноженные на -1, получим матрицу 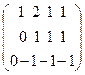. Теперь к элементам 3-ей строки прибавим элементы 2-ой строки: 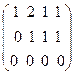. Вычеркнем 3-ю строку: 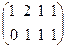- ступенчатая матрица, эквивалентная матрице А. Видим, что в ней две строки, поэтому ранг матрицы А равен 2.

Немецкий математик Кронекер Л. (1823-1891) и итальянский математик Капелли доказала следующую теорему.

Теорема 4 (Кронекера-Капелли). Система (3.1) m линейных уравнений с n неизвестными имеет решение тогда и только тогда, когда матрица системы и расширенная матрица системы имеют один и тот же ранг.

Доказывать теорему не будем.

Таким образом, из теорем 4 и 1 следует, что: 1) если ранг расширенной матрицы системы (3.1) больше ранга матрицы системы, то система решения не имеет, т.е. система (3.1) несовместна; 2) если эти ранги равны, но меньше n, то система (3.1) совместна и имеет бесконечно много решений, т.е. является неопределенной; 3) если ранги матрицы системы и расширенной матрицы системы равны и равны числу неизвестных n, то система (3.1) имеет единственное решение, которое находится по формулам Крамера (3.4). Других возможностей нет, так как ранг расширенной матрицы системы не может быть меньше матрицы системы.

Как искать решения системы (3.1) во втором случае? Это можно сделать по формулам Крамера, выбрав из системы (3.1) число уравнений, равное рангу матрицы системы, и решить полученную систему уравнений. Можно воспользоваться также методом Гаусса (методом исключения неизвестных).

Пример 3. Решим систему уравнений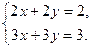

Решение. Матрица системы 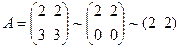, т.е. имеет ранг, равный 1.

Расширенная матрица системы 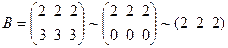тоже имеет ранг, равный 1, т.е. ранги матрицы системы и расширенной матрицы системы равны, но меньше числа неизвестных. Поэтому оставляем одно уравнение системы 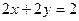, из которого находим 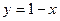, т.е. решение данной системы имеет вид 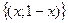, где х принимает произвольные значения, т.е. данная система имеет бесконечно много решений. Ответ: .

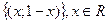Пример 4. Решим систему уравнений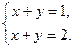

Решение. Матрица системы 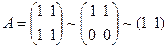, т.е. имеет ранг, равный 1. Расширенная матрица системы имеет ранг, равный 2. Ранги не равны, поэтому система уравнений несовместна, т.е. решения не имеет.

Пример 5. Решим систему уравнений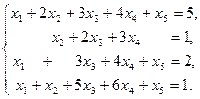

Решение. Найдем сначала ранги матрицы системы 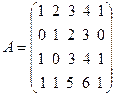и расширенной

матрицы системы 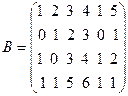. Для этого приведем расширенную матрицу системы к ступенчатому виду с помощью элементарных преобразований. Вычтем из элементов 3-ей и 4-ой строк соответствующие элементы 1-ой строки, получим 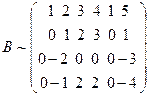. Прибавим теперь к элементам 3-ей строки соответствующие элементы 2-ой строки, умноженные на 2, а к элементам 4-ой строки соответствующие элементы 2-ой строки: 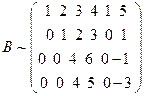. Вычтем из элементов 4-ой строки соответствующие элементы 3-ей строки: 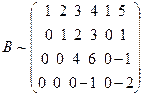. Видим, что ранг расширенной матрицы В равен четырем, ранг матрицы системы А тоже равен четырем, так как 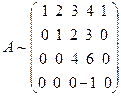. При этом неизвестных пять, т.е. больше ранга матрицы системы. Поэтому одно (пятое, так как определитель системы с первыми четырьмя неизвестными равен -4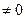) неизвестное перенесем в правую часть уравнений системы и полученную систему (которая равносильна данной, так как элементарные преобразования мы проводили только над строками матрицы, т.е. над уравнениями системы)нкоторая равносильна данной, так как преобразования мы проводили только над строками матрицы, т.ицы системы, и решить полученну 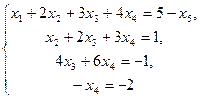решаем либо по формулам Крамера, либо методом Гаусса, что проще. Воспользуемся методом Гаусса. Для этого находим 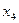из последнего уравнения системы и подставляем в остальные уравнения (исключаем из них 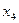, отсюда название – метод исключения неизвестных), получим 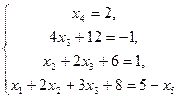или 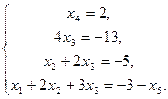Теперь из 2-го уравнения находим 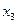и подставляем в 3-е и 4-е уравнения:

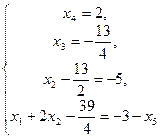или 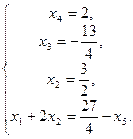Из 3-го уравнения находим и подставляем в 4-е уравнение: 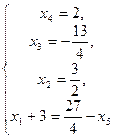или 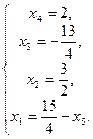Наконец, находя из 4-го уравнения системы 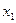, получим решение исходной системы 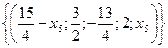, в котором неизвестное 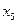принимает произвольные значения, т. е. получаем бесконечно много решений данной системы уравнений. Это решение называют также общим решением данной системы уравнений. При конкретных значениях 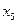получаем частные решения данной системы. Например, если 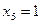, то 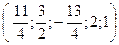- частное решение данной системы уравнений.

Карл Фридрих Гаусс (1777-1855) – выдающийся немецкий математик. Родился в г. Брауншвейге. Сын поденщика. Начал делать открытия в 16-летнем возрасте. В книге Д.Я. Стройка «Краткий очерк истории математики» он назван вундеркиндом, юным гением, его роль в математике сравнивается с ролью Гегеля в философии, Бетховена в музыке, Гете в литературе.

В заключение параграфа заметим, что систему (3.1) можно записать в матричной форме

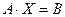, (3.6)

где А = 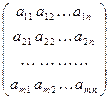– матрица системы, 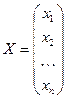– матрица-столбец неизвестных, 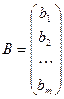– матрица-столбец свободных членов. Если 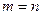, то для решения матричного уравнения (3.6) нужно найти матрицу 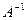, такую, что 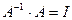. Умножив уравнение (3.6) на 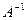слева, получим 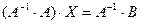, откуда 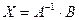– решение матричного уравнения (3.6). Приравнивая соответствующие элементы матриц Х и 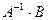, получим решение системы (3.1) (при ).

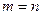Определение 10. Матрица 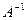, для которой 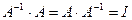, называется обратной матрицей к квадратной матрице А.

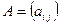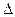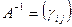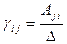В алгебре доказывается, что для матрицы , определитель которой не равен нулю, обратной матрицей является матрица , где , а 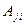– алгебраическое дополнение элемента .

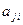Пример 6. Решим систему уравнений примера 1 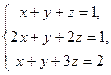матричным методом.

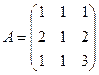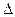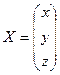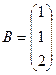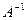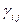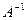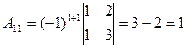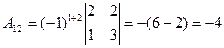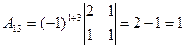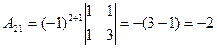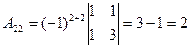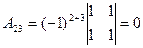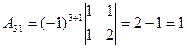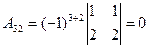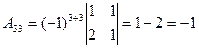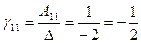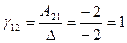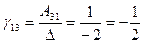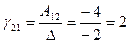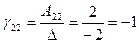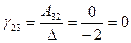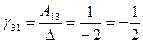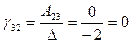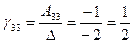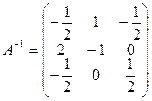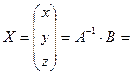
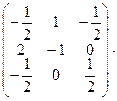
Решение. Имеем – матрица системы, = –2 (см. решение примера 1), – матрица-столбец неизвестных, – матрица-столбец свободных членов. Найдем обратную матрицу . Для этого сначала вычислим алгебраические дополнения элементов матрицы А, а затем элементы матрицы . Имеем , , , , , , , , , , , , , , , , , . Таким образом, матрица . Теперь найдем 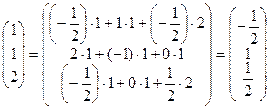. Отсюда находим 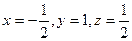. Ответ: .

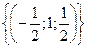Дата добавления: 2013-12-12