
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Модуль действительного числа
|
|
|
|
Множества. Операции над множествами. Числовые множества
Глава III. ЧИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
Определение множества не дается. Это понятие первичное, неопределяемое. Необходимость таких понятий вызвана тем, что любое понятие определяется через какое-то другое понятие, введенное ранее, которое в свою очередь определяется через понятие, введенное еще раньше. Ясно, что продолжать этот процесс бесконечно мы не можем, поэтому надо ввести неопределяемое понятие. В школе такими понятиями были, кроме понятия множества, понятия точки, прямой и плоскости. Понятие множества поясняется на примерах. Множество считается заданным, если указаны элементы, из которых оно состоит.
Например, множество натуральных чисел N = {1;2;…; n;…}, множество А = {2;5;7}, множество С студентов группы ФМО–11, и т.д.
Тот факт, что число 2 принадлежит множеству А, записывается короче так: 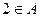 , а то, что стол не принадлежит множеству А, следующим образом: стол
, а то, что стол не принадлежит множеству А, следующим образом: стол 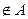 , или, например,
, или, например, 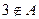 .
.
Определение 1. Множество называется конечным, если оно состоит из конечного числа элементов. Множество, не являющееся конечным, называется бесконечным. Множество, не содержащее ни одного элемента, называется пустым и обозначается символом ø.
Конечное множество можно задать перечислением всех его элементов. Например, множество студентов группы ФМО–11 задается списком в журнале, множество А задано перечислением всех его элементов – чисел 2, 5 и 7. Множество N натуральных чисел – бесконечное.
Определение 2. Множества называются равными, если они состоят из одних и тех же элементов.
Например, равны множества А = {2;5;7} и В = {5;7;2}. Все пустые множества равны между собой.
Определение 3. Множество 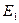 называется подмножеством (или частью) множества
называется подмножеством (или частью) множества 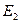 , если из того, что элемент
, если из того, что элемент 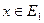 следует, что
следует, что 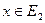 :
: 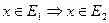 . Записывается это так:
. Записывается это так: 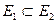 .
.
Например, 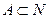 . Пустое множество – часть любого множества.
. Пустое множество – часть любого множества.
Множества могут быть и несравнимыми. Таковы, например, множества А и С, так как ни одно из этих множеств не является подмножеством другого множества.
Определение 4. Объединением двух множеств 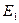 и
и 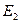 называется множество Е, состоящее из всех элементов множеств
называется множество Е, состоящее из всех элементов множеств 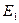 и
и 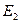 и только из них:
и только из них: 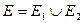 .
.
Например, если 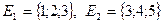 , то
, то 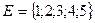 ,
, 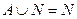 .
.
Определение 5. Пересечением множеств 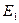 и
и 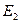 называется множество Е, состоящее из всех общих элементов множеств
называется множество Е, состоящее из всех общих элементов множеств 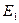 и
и 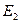 :
: 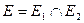 .
.
Например, для рассмотренных выше множеств 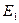 и
и 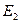
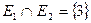 ,
, 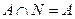 .
.
Определения 4 и 5 переносятся на любое конечное число множеств. Например, 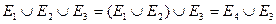 , где
, где 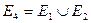 . С помощью метода математической индукции эти определения можно перенести и на бесконечное число множеств.
. С помощью метода математической индукции эти определения можно перенести и на бесконечное число множеств.
Определение 6. Разностью множеств 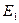 и
и 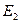 называется множество вех элементов множества
называется множество вех элементов множества 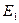 , не принадлежащих множеству
, не принадлежащих множеству 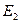 :
: 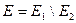 .
.
Например, {1;2;3;4}{4;5;6}={1;2;3}, А N = ø.
В математическом анализе мы будем иметь дело, в основном, с множествами
действительных чисел. Из школьного курса математики известны множества натуральных чисел N = {1;2;…; n;…}, целых чисел 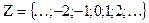 , рациональных чисел
, рациональных чисел 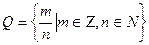 , иррациональных чисел I. Известно также, что множество всех действительных чисел R =
, иррациональных чисел I. Известно также, что множество всех действительных чисел R = 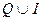 . В высшей математике имеютсястрогие теории действительных чисел, например, теория Дедекинда (1831-1916, немецкий математик), из которой получаются свойства множества R действительных чисел, которыми мы будем пользоваться в дальнейшем: упорядоченность по величине, плотность, усиленная плотность, непрерывность (или полнота).
. В высшей математике имеютсястрогие теории действительных чисел, например, теория Дедекинда (1831-1916, немецкий математик), из которой получаются свойства множества R действительных чисел, которыми мы будем пользоваться в дальнейшем: упорядоченность по величине, плотность, усиленная плотность, непрерывность (или полнота).
Упорядоченность по величине множества R: для любых двух действительных чисел 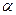 и
и 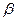 имеет место одно и только одно из соотношений:
имеет место одно и только одно из соотношений: 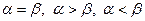 .
.
Плотность множества R: между любыми двумя различными действительными числами содержится действительное число.
Усиленная плотность множества R: между любыми двумя различными действительными числами содержится рациональное число.
Непрерывность (полнота) множества R: для любой системы вложенных отрезков 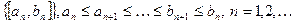 существует хотя бы одно число, принадлежащее всем отрезкам данной системы. Если длины
существует хотя бы одно число, принадлежащее всем отрезкам данной системы. Если длины 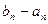 вложенных отрезков стремятся к нулю при
вложенных отрезков стремятся к нулю при 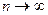 , то существует единственная точка, принадлежащая всем этим отрезкам. Это свойство называется также принципом вложенных отрезков Кантора (Георг Кантор (1845-1918), немецкий математик).
, то существует единственная точка, принадлежащая всем этим отрезкам. Это свойство называется также принципом вложенных отрезков Кантора (Георг Кантор (1845-1918), немецкий математик).
При аксиоматическом определении множества действительных чисел свойства упорядоченности по величине и непрерывности (полноты) включаются в число аксиом.
Действительные числа изображаются, как известно, точками числовой прямой, причем каждому действительному числу соответствует одна точка числовой прямой и обратно, каждой точке числовой прямой соответствует только одно действительное число. Как говорят, установлено взаимно-однозначное соответствие между множеством точек числовой прямой и множеством действительных чисел.
Из школьного курса математики известны также некоторые специальные числовые множества: 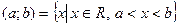 - интервал (открытый промежуток),
- интервал (открытый промежуток), 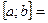
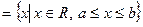 - отрезок (замкнутый промежуток),
- отрезок (замкнутый промежуток), 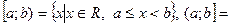 =
=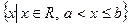 - полуинтервалы (открытый справа и слева соответственно),
- полуинтервалы (открытый справа и слева соответственно), 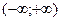 - вся числовая прямая,
- вся числовая прямая, 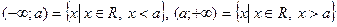 - лучи. Нам потребуется в дальнейшем еще понятие окрестности точки.
- лучи. Нам потребуется в дальнейшем еще понятие окрестности точки.
Определение 7. Если а – некоторое действительное число, 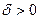 - любое положительное действительное число, то интервал
- любое положительное действительное число, то интервал 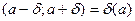 называется
называется 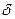 - окрестностью точки а. Точка а называется центром окрестности, а число
- окрестностью точки а. Точка а называется центром окрестности, а число 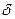 - радиусом окрестности. Множество
- радиусом окрестности. Множество 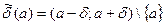 называется проколотой
называется проколотой 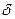 - окрестностью точки а.
- окрестностью точки а.
Определение 8. Множество Е действительных чисел называется ограниченным сверху (соответственно, ограниченным снизу), если существует число М, такое, что для любого 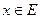 имеет место неравенство
имеет место неравенство 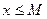 (соответственно,
(соответственно, 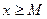 ). Число М называется верхней (соответственно, нижней) границей (или гранью) множества Е. Множество Е называется ограниченным, если существуют такие числа
). Число М называется верхней (соответственно, нижней) границей (или гранью) множества Е. Множество Е называется ограниченным, если существуют такие числа 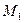 и
и 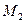 , что для любого числа
, что для любого числа 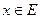 имеет место двойное неравенство
имеет место двойное неравенство 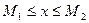 .
.
Например, множество правильных дробей ограничено сверху числом 1, множество N натуральных чисел ограничено снизу числом 1, множество 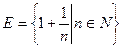 ограничено, так как
ограничено, так как 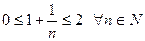 .
.
Заметим, что если М – верхняя граница непустого ограниченного сверху числового множества Е, то любое число, большее М, также будет его верхней границей, то есть у Е есть бесконечное множество верхних границ. Из всех верхних границ множества Е наибольший интерес представляет его наименьшая верхняя граница.
Определение 9. Наименьшая из верхних границ множества Е называется его точной верхней границей (или точной верхней гранью) и обозначается sup E ( от латинского слова supremum – наивысшее).
Аналогично вводится понятие точной нижней границы множества Е, ограниченного снизу.
Определение 10. Наибольшая из нижних границ множества Е называется его точной нижней границей (или точной нижней гранью) и обозначается inf E ( от латинского слова infimum – наинизшее).
Имеет место
Теорема. Всякое непустое и ограниченное сверху (соответственно, снизу) числовое множество Е имеет точную верхнюю (соответственно, нижнюю) границу.
Без доказательства.
Определение. Абсолютной величиной (или модулем) действительного числа 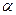 (обозначается
(обозначается 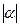 ) называется неотрицательное число, удовлетворяющее условиям:
) называется неотрицательное число, удовлетворяющее условиям:
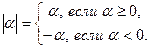
Ясно, что всегда
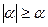 . (2.1)
. (2.1)
Свойства абсолютных величин:
1) 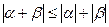 ; 2)
; 2) 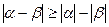 ; 3)
; 3) 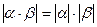 ; 4)
; 4) 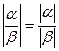 .
.
Доказательство. 1) Если 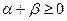 , то
, то 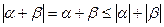 в силу (2.1). Если
в силу (2.1). Если 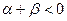 , то
, то 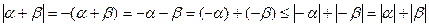 . Первое свойство доказано.
. Первое свойство доказано.
2) Имеем 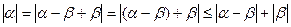 , отсюда
, отсюда 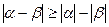 . Второе свойство доказано.
. Второе свойство доказано.
3) 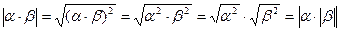 , третье свойство доказано.
, третье свойство доказано.
Четвертое свойство доказывается так же, как свойство 3).
Замечание. Свойство 1) распространяется на любое число слагаемых, свойство 3) – на любое число сомножителей.
Отметим также, что 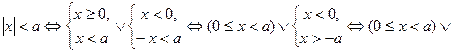
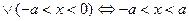 , т.е. х удовлетворяет неравенству
, т.е. х удовлетворяет неравенству 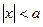 тогда и только тогда, когда принадлежит интервалу
тогда и только тогда, когда принадлежит интервалу 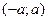 .
.
Геометрический смысл модуля действительного числа состоит в том, что 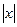 равен расстоянию от точки х на числовой прямой до нуля.
равен расстоянию от точки х на числовой прямой до нуля.
|
|
|
|
Дата добавления: 2013-12-12; Просмотров: 1099; Нарушение авторских прав?; Мы поможем в написании вашей работы!