Этапы составления и исследования моделей

Классификация моделей

Основные понятия.

Конспект лекций по моделированию систем

Выполнил студент:

группы ИТ-424

Вафина И. А.

Преподаватель:

Замыслов В.Е.

2007 г.

Содержание:

§ 1. Основные понятия. 3

§ 2. Классификация моделей. 5

§ 3. Этапы составления и исследования моделей. 6

§ 4. Имитационное моделирование. 8

§ 5.Элементы теории вероятности. 10

Способы вычисления вероятности. 10

§ 6.Примеры основных случайных величин и их характеристик. 14

§ 7.Построение датчика псевдослучайных чисел. 16

§ 7.1 Датчики для равномерного закона распределения. 16

§ 7.2 Построение датчика псевдослучайных чисел для любого закона распределения 16

§ 7.3 Построение датчика по показательному закону распределения. 17

§ 7.4 Построение датчика с помощью таблицы квантилей. 18

§ 8. Потоки случайных событий. Пуассоновский поток. 19

§ 9.Связь потока Пуассона с показательным законом распределения. 21

§ 11. Моделирование работы конечного автомата. 24

§12. Моделирование работы системы массового обслуживания. 27

§ 13. Двумерные случайные величины и их законы распределения. 34

§ 14.Понятие зависимых и независимых случайных величин. 36

§15 Условное математическое ожидание линии регрессии. 38

§16 Числовые характеристики двумерных случайных величин. 39

Корреляционный момент. 39

§17 Виды зависимости между случайными величинами. 42

§18 Нахождение на практике линейной регрессии. 45

Понятия модели и моделирования.

Для определения этих понятий необходимо рассмотреть следующие задачи:

Задача №1

По рельсу катиться колесо, нужно определить какие силы действуют на колесо

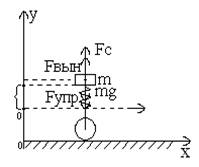
Fупр=-k1·y(t) жесткость пружины- закон Гука

Fс=-k2·y’(t)

2 закон Ньютона

my’(t)= k1·y(t)-k2·y’(t)-mg+Fвын

my’’(t)+k2·y’(t)-k1·y(t)=-mg+Fвын

Задача №2

Происходит колебание тока, ток идет в двух направлениях

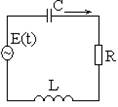
По закону Ома:

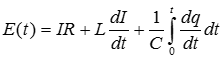
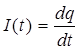
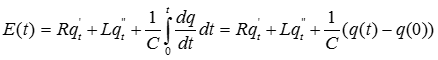
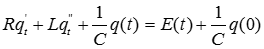
Эти уравнения фактически одинаковы, т.е. для двух разных систем уравнения, описывающие колебания фактически одинаковы. Следовательно, механическую систему можно изучить при помощи элементарных систем и наоборот.

Принцип позволяющий представлять сложные системы при помощи простых – это и есть моделирование.

Пусть есть система А, которая обладает набором свойств S, моделью данной системы будем называть А’. Она будет обладать аналогичным набором свойств S’ похожих на S. При изучении мы можем заменить А с S на А’ с S’ – эту систему называют моделью.

Процесс моделирования – это построение модели для механических систем и изучение свойств модели.

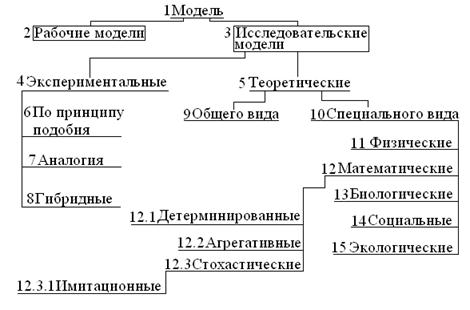
Рабочие модели (искусственное сердце, печень, почки – это модели копирующие основные свойства органов) – это системы обладающие теми же свойствами, предназначены не для изучения, а для замены.

Исследовательские модели – созданы для изучения свойств исходного объекта, которого сложно изучать.

Экспериментальные модели – это реальные системы, которые обладают свойствами исходной системы.

Подобие (по внешним признакам) для изучения свойств зависящих от внешних признаков (моделируется только форма, например, самолет).

Аналогия – системы внешне разные, но обладают аналогичными свойствами.

Гибридные – такие модели сочетают и аналогию и подобие (например, обучение пилота перед монитором, т.е. подобие – кабина, аналогия – реакция модели на действие пилота).

Теоретические модели – модель существует теоретически на бумаге или в компьютерном виде.

Общего вида – глобальные теории (всемирного тяготения и т.д.) охватывают общие свойства окружающего мира.

Специальные теории – теории в отдельных областях знаний.

Детерминированные – эти модели описываются при помощи дифференциальных уравнений.

Стохастические – это модели, в которых применяются методы теории вероятности поведения таких систем на постоянное воздействие и присутствуют различные результаты.

Агрегативные модели – это модели, которые допускают декомпозицию на более простые модели.

1) Составление физической модели. Используются принципы идеализации и абстрагирования

Идеализация – это упрощение свойств изучаемых объектов.

Пример:

F=-k·x

Рассматривается идеальная пружина и на всей поверхности действует закон Гука.

Абстрагирование – это отбрасывание некоторых свойств объекта

Пример: пренебрежение трением или давлением воздуха.

2) Составление математической модели - это описание свойств физической модели в математических терминах.

Пример: описание дифференциальными уравнениями.

3) Исследование математической модели математическими средствами.

4) Интерпретация полученных результатов (отношение с физическим и реальным объектом).

5) Определение и оценка точности совпадения полученных результатов в результате моделирования со свойствами реальных объектов.

Пример:

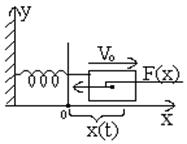
Толкнули груз и он начал колебаться

1) M – материальная точка массы m, действует закон Гука.

F= -k·x, где x – отклонение,

k – жесткость.

Пренебрегаются трение и сопротивление воздуха.

2) Составляются дифференциальные уравнения

Положение груза в момент времени t - x(t)

x’(t) = V

x’(0) = V₀

F(x)= -k·x

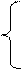Записывается второй закон Ньютона:

mx”(t) = -k·x;

x(0) = 0;

x’(0) = V₀.

3) Решение уравнений

mx”(t) + k·x=0

mλ² + k·1=0

λ² =-(k/m)

λ_1,2 = ±√(k/m)

x(t)=c₁sin(βt) + c₂cos(βt)

x(0) = 0 = c₁0+ c₂1, => c₂=0

x(t) = c₁sin(βt)

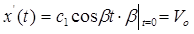
c₁β·1=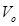

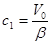
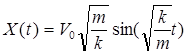- уравнение колебания

4) Получили синусоидальное колебание

,

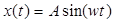
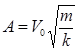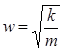
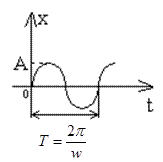
5) Реального объекта нет, но совпадения будут лучше, если модель будет точнее

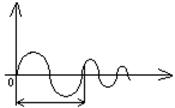
§ 4. Имитационное моделирование.

4.1 Статистический эксперимент

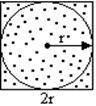Задача: определить значение числа π, бросая камешки.

Бросаем камешки, находясь на расстоянии в квадрат, при этом они равномерно распределены в квадрате.

N – попали в квадрат

k – попали в круг

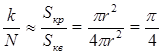
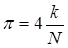
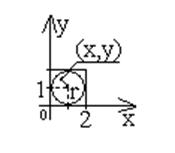
Составим программу, которая покажет, сколько камешков нужно бросить.

N=100

k=10

for n=1:N

x=2·random;

y=2·random;

r=sqrt((x-1)²+ (y-1)²)

if r<=1

k=k+1

end

end

p=4*k/N;

Каждый прогон этой программы для разных N выполняет некий статистический эксперимент. Эта программа есть математическое описание имитационной модели.

4.1 Определение имитационной модели

Имитационная модель – это формальное, т.е. выполненное на формальном языке, описание логики функционирования исследуемой системы и взаимодействие отдельных её элементов во времени, учитывающее наиболее существенные причинно-следственные связи, присущие системе, обеспечивающие проведение статистического эксперимента.

Отсутствует ограничение по применению и речь может идти только о целесообразности применения. Наибольший эффект применения имитационных моделей, у которых на функционирование оказывают влияние внешние факторы.

Применение имитационного моделирования целесообразно в следующих случаях:

- можно найти аналитическую зависимость выходных параметров системы от количественных характеристик внешних факторов;

- можно находить оптимальные параметры функционирования модели или системы;

- если есть влияние внешних факторов на поведение модели и системы, которое она моделирует.

Дата добавления: 2013-12-12