Минимизация конечных автоматов

Связь потока Пуассона с показательным законом распределения

Пусть существует Пуассоновский поток

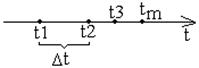Δt – непрерывная случайная величина

Теорема:

Промежуток времени между двумя соседними событиями Пуассоновского потока есть случайная величина, имеющая показательный закон распределения с тем же показателем λ – что и Пуассоновского потока и наоборот.

Дано: поток простейший.

Доказательство:

Δt - промежуток времени между двумя соседними событиями имеет показательный закон распределения с тем же параметром λ.

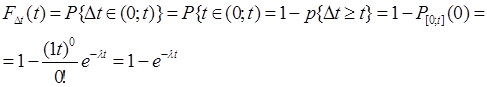
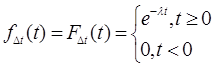
Теорема доказана.

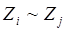- два состояния конечного автомата эквивалентны, если при воздействии на автомат любой последовательности входных сигналов получаем одинаковую последовательность выходных сигналов.

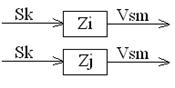
Алгоритм эквивалентных пар

Алгоритм начинается с построения таблицы эквивалентных пар

Автоматная таблица:

Z	S	α	β	γ	α	β	γ

По автоматной таблице составляем таблицу пар:

Таблица 1.

		α	β	γ
	1,3	2,2	2,2	5,5
*	1,5	2,6	2,4	5,3
*	1,7	2,6	2,2	5,8
	1,8	2,4	2,4	5,7
	2,4	1,3	4,2	4,2
+	2,6	1,8	4,9	4,6
º	2,9	1,7	4,9	4,7
*	3,5	2,6	2,4	5,3
*	3,7	2,6	2,2	5,8
	3,8	2,4	2,4	5,7
+	4,6	3,8	2,9	2,9
º	4,9	3,7	2,9	2,7
	5,7	6,6	4,2	3,8
*	5,8	6,4	4,4	3,7
º	6,9	8,7	9,9	6,7
*	7,8	6,4	2,4	8,7

(2,9), (4,9), (6,9) дальше не будут давать эквивалентные значения на выходе.

Таблица 2.

1~3	1~3~8
1~8	2~4
2~4	5~7
3~8
5~7

Алгоритм минимизации:

1) Составление таблицы пар, для которых выходные сигналы одинаковы, и заполнение этой таблицы парами, которые переходят в пары первого столбца при первом входном сигнале.

2) Отмечаются строчки таблицы, в которых есть различимые пары, отсутствующие в первом столбце. Различимая пара – это пара, в которой два разных состояния. Отметить строчку – это, значит, отметить пару первого столбца этой строки. (Этот шаг повторяется в цикле)

3) Отмечают строчки, в которых есть пары отмеченные в первом столбце. Эквивалентными будут те пары, которые остались не отмеченные.

Составим автоматную таблицу для состояний 1-5.

Таблица. 3

	α	β	γ	α	β	γ

1) Берем ст. 1 из строящейся табл. 3

2) Смотрим из табл.2 какие цифры соответствуют.

3) Из табл.1 выбираем по полученным цифрам строки и по табл.2 в табл.3 записываем полученные состояния.

Дата добавления: 2013-12-12