Пользуясь формулой, вычисляем накопленные частоты интервалов. В частности,

Таблица 1

Объем выборки n	30 - 50	50 - 90	100 - 200	300 - 400
Число интервалов k	5 -6

Процедура получения интервального вариационного ряда состоит из следующих шагов.

1. Пользуясь табл. 1, находят число интервалов .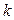

2. Определяют длину интервала:

3. Находят границы интервалов.

4. Находят частоты интервалов.

5. Полученные результаты заносят в таблицу.

Интервальный статистический ряд наглядно может быть представлен в виде гистограммы частот – столбиковой диаграммы, состоящей из прямоугольников, основаниями которых служат подынтервалы, а высота равна 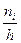(плотность частоты). Площадь i -го прямоугольника равна 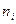, а площадь всей гистограммы частот равна сумме всех частот, т.е. объёму выборки .

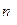Для построения гистограммы относительных частот основание прямоугольника также равно h, а высота 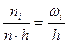. Площадь каждого столбика равна 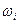. Площадь всей гистограммы относительных частот равна .

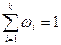На основании гистограммы обычно выдвигается предположение о виде закона распределения исследуемой величины.

Пример 2. Анализируется доход населения. Извлечена выборка объёма 300 единиц. По уровню дохода население подразделяется на 6 групп. Данные сгруппированы в интервальный статистический ряд:

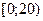
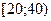
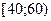
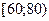
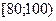
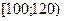
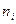
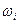
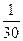
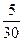
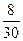
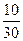
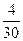
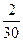
Построить гистограмму относительных частот.

Решение. Шаг h = 20. Разделив относительные частоты на шаг разбиения, получим высоту столбиков.

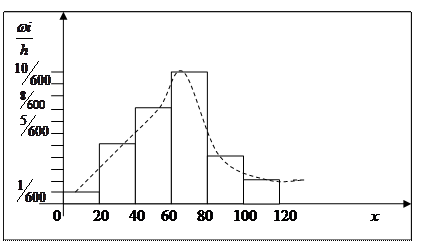
Форма гистограммы в наибольшей степени соответствует нормальному распределению.

Пример 3. Мальчиками 12 - 13 лет были показаны следующие результаты в подтягивании на перекладине:

9, 5, 7, 10, 11, 10, 14, 7, 10, 11, 8, 10, 8, 9, 12, 13, 8, 11, 9, 9, 10, 6, 9, 13, 9, 17, 11, 15, 8, 14, 11, 16, 8, 10, 10, 11, 8, 9, 10, 10, 8, 11, 14, 12, 11, 13, 15, 13, 10, 5.

Требуется представить данную неупорядоченную выборку в виде интервального вариационного ряда.

Решение. Непосредственным подсчетом находим объем выборки: .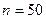

1. Пользуясь табл. 1, определяем число интервалов. Полагаем .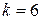

2. Просматривая заданный ряд, замечаем, что максимальное число подтягиваний равно 17 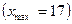, а минимальное - 5 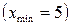. Пользуясь формулой, находим длину интервала .

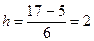3. Находим границы интервалов.

К границам предыдущего интервала прибавляем длину интервала 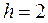. В частности,

, .

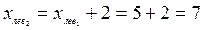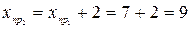Замечаем при этом, что правая граница первого интервала является левой границей второго интервала. И так далее до тех пор, пока не найдем: .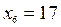

4. Считаем частоты каждого интервала, отыскивая в заданном ряду значения, удовлетворяющие неравенству:

, .

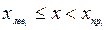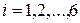В частности, для первого интервала таких значений три, для второго - девять и т. д., то есть

, , , , , .

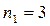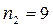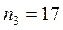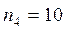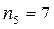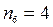Полученные данные заносим в таблицу (см. табл. 2, первые три столбца); им же соответствует рис.

;

;

;

.

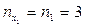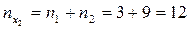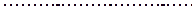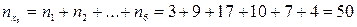6. Вычисляем частости интервалов. Например,

; ; .

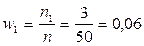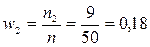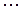7. Вычисляем накопленные частости интервалов.

8. Данные вычислений заносим в табл. 2

Таблица 2

№ интервала	Границы интервала	Частота	Накопленная частота	Частость	Накопленная частость
	5 - 7			0,06	0,06
	7 - 9			0,18	0,24
	9 - 11			0,34	0,58
	11 - 13			0,20	0,78
	13 - 15			0,14	0,92
	15 - 17			0,08

Распределение типа сведенного в табл. 2 представляет собой интервальный вариационный ряд.

Анализ вариационных рядов упрощается при их графическом представлении. Наряду с гистограммой и полигоном частот можно построить полигон накопленных частостей (кумулята)

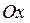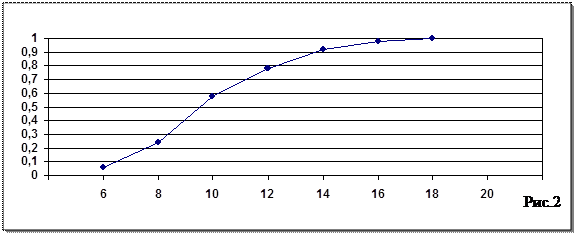
График получается при соединении точек прямыми отрезками. Координаты точек соответствуют верхним границам интервалов и накопленным частотам. Если по оси ординат откладывать накопленные частости, то полученный график называется полигоном накопленных частостей. Если ряд не интервальный, то по оси откладывают значения измеряемого признака, а по оси - соответствующие накопленные частоты или частости. На рис.2 изображен полигон накопленных частостей для примера 3.

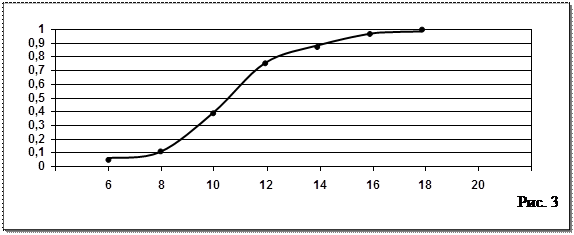
На практике соседние точки чаще всего соединяют кривыми линиями (рис. 3).

1.3. Статистические характеристики вариационного ряда

Для полноты картины анализа выборки рассматривают статистические характеристики вариационного ряда. С этой целью оценивают следующие качества ряда:

ü центральную тенденцию выборки;

ü вариацию.

Центральную тенденцию выборки оценивают такими статистическими характеристиками, как

ü мода;

ü медиана;

ü среднее арифметическое значение.

К характеристикам вариации относят:

ü размах;

ü дисперсию;

ü среднее квадратическое отклонение;

ü коэффициент вариации;

ü ошибку выборочного среднего.

Модой называется значение признака, наиболее часто встречающееся в выборке. Мода обозначается 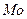. Если значения выборки сгруппированы в интервальный вариационный ряд, то выбирается модальный интервал с наибольшей частотой.

Медиана - это такое значение признака, при котором одна половина значений признака меньше ее, а другая половина - больше (медиана делит вариационный ряд пополам). Медиана обозначается 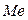. Для отыскания медианы выборку ранжируют, то есть значения признака располагают в порядке возрастания или убывания. В ранжированной выборке ранг (порядковый номер в выборке) 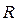медианы определяют по формул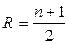е: , где 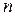- объем выборки.

При 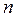нечетном ранг 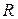- целое число, и медианой считают следующее значение: 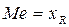. При 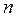четном ранг 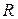- число не целое, представимое в ви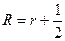де , где 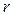- целое. В таком случае медианой считают значение .

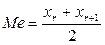Среднее арифметическое неупорядоченной выборки вычисляют по формуле:

.

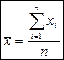В случае интервального вариационного ряда формула приобретает вид: 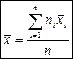, где 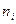- частота 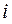-го интервала, 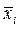- среднее арифметическое значение этого интервала.

Размах вариации – это разность между максимальным и минимальным значениями выборки:

.

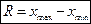Дисперсией называется средний квадрат отклонений значений признака от среднего арифметического и вычисляется по формуле:

.

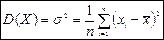Средним квадратическим отклонением называется положительный квадратный корень из дисперсии:

,

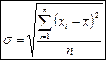Среднее квадратическое отклонение имеет ту же единицу измерения, что и варьирующий признак. Оно характеризует степень отклонения значений признака от его среднего арифметического значения в абсолютных единицах.

Для сравнения варьируемости двух или нескольких выборок, имеющих разные единицы измерения, используют коэффициент вариации. Коэффициент вариации - это относительный показатель, равный отношению среднего квадратического отклонения к среднему арифметическому значению:

.

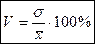Принято считать, что если 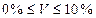, то варьируемость малая, 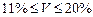- средняя, 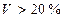- большая.

Отклонения выборочных коэффициентов от параметров в генеральной совокупности называются ошибками параметров. Эти ошибки возникают в силу того, что выборочная совокупность представляет генеральную совокупность только приближенно. Если взять несколько вариантов выборок объемом 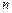из одной и той же генеральной совокупности и вычислить для каждой из них среднее арифметическое, то окажется, что средние арифметические выборок варьируют вокруг среднего арифметического для генеральной совокупности 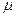в 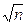раз меньше, чем отдельные варианты. На этом основании в качестве стандартной ошибки выборочного среднего принимают величину

.

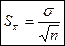Чтобы подчеркнуть точность оценки среднего выборочного, его чаще всего записывают в виде: .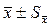

Пример 4. В качестве оценки силовой подготовки учащихся 5 класса произведен тест на количество подтягиваний на перекладине.

Данные теста следующие: 9, 9, 10, 11, 8, 7, 10, 7, 9, 11, 7, 8, 9, 8, 9.

Требуется вычислить моду, медиану, среднее арифметическое значение, размах вариации, дисперсию, среднее квадратическое отклонение, коэффициент вариации и ошибку выборочного среднего данной выборки.

Решение. Непосредственным подсчетом убеждаемся, что значение 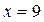встречается в выборке чаще других (5 раз), следовательно, .

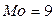Для вычисления медианы производим ранжировку заданной выборки:

7, 7, 7, 8, 8, 8, 9, 9, 9, 9, 9, 10, 10, 11, 11

Объем выборки 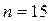- число нечетное, поэтому ранг медианы вычисляем по формуле:

,

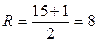то есть медианой является 8-е значение выборки), .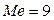

Среднее арифметическое значение выборки находим, пользуясь формулой:

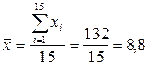
Крайние значения ряда) определяют минимальное и максимальное значения выборки 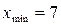, 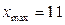. Согласно определению, размах вариации равен:

.

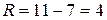Для удобства вычисления дисперсии составляем таблицу. Пользуясь суммой значений последней колонки и формулой, находим: .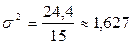

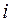
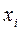
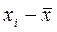
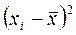
		0,2	0,04
		0,2	0,04
		1,2	1,44
		2,2	4,84
		-0,8	0,64
		-1,8	3,24
		1,2	1,44
		-1,8	3,24
		0,2	0,44
		2,2	4,24
		-1,8	3,24
		-0,8	0,64
		0,2	0,04
		-0,8	0,64
		0,2	0,04
S			24,4

Вычислим среднее квадратическое отклонение: .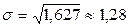

Коэффициент вариации: 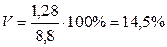, откуда делаем вывод - результаты тестирования имеют средний коэффициент вариации.

Ошибку выборочного среднего арифметического находим: .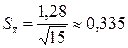

Наконец, записываем: .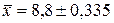

Дата добавления: 2013-12-12