Интегрирование рациональных функций

1 ) Многочлен. Понятие о рациональных функциях

Функция вида 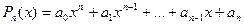-, как говорилось ранее, называется многочленом (или целой рациональной функцией). Всякий многочлен должен иметь по крайней мере один корень, действительный или мнимый(корнем многочлена называется такое значение х₀ переменной х, при котором многочлен 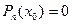). Очевидно, что всякий многочлен 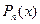можно представить в виде 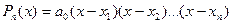, где х₁, х₂, … х_n – корни многочлена, 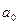– коэффициент при хⁿ. Множители (х-х₁) в записанном соотношении называются линейными множителями.

Пример: Разложить многочлен 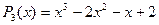на множители. Корни этого многочлена х₁=-1, х₂=1, х₃=2, следовательно .

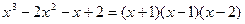Можно доказать, что многочлен с действительными коэффициентами разлагается на линейные и квадратные множители с действительными коэффициентами, т.е. многочлен 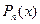можно предоставить в виде:

……

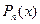
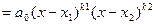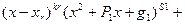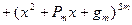
при этом 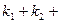…, все квадратные трехчлены не имеют вещественных корней.

Пример: .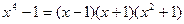

2) Дробно-рациональная функция

Дробно-рациональной функцией называется функция равная отношению двух многочленов, т.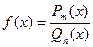е. , где 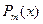- многочлен степени m, а 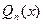- многочлен степени n. Рациональная дробь называется правильной, если степень числителя меньше степени знаменателя, т.е. m<n. В противном случае, если m>n, то дробь называется неправильной. Всякую неправильную рациональную дробь 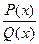- путем деления числителя на знаменатель можно представить в виде суммы многочлена 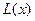и правильной рациональной дроби 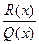, т.е. =+.

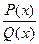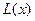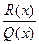Например:

=;

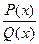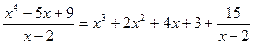Результат получен при делении столбиком 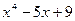на 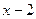, где 15 – остаток деления.

Всякую правильную рациональную дробь можно представить (и причем единственным образом) в виде следующей суммы простейших дробей:

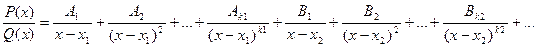
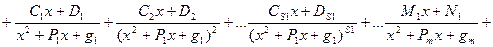
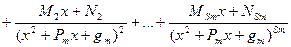, где 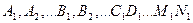- некоторые действительные коэффициенты.

Примеры:

1. ;

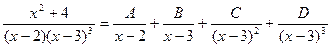2. .

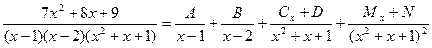Для нахождения неопределенных коэффициентов 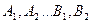используют метод сравнения коэффициентов. Суть метода следующая. Правую часть разложения дроби 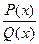приводим к общему знаменателю. В результате получим тождество 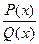=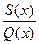, где S(x) – многочлен с неопределенными коэффициентами. Т.к. знаменатели равны, то тождественны и числители, т.е. P(x)=S(x).

Приравнивая коэффициенты при одинаковых степенях x, получим систему уравнения, решая которую и определим коэффициенты .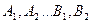

Пример:

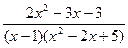- представить дробь в виде суммы простейших дробей. Согласно сказанному раннее, получим 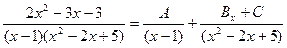, т.е.

;

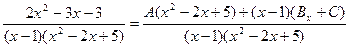отсюда 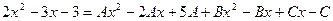, т.е. .

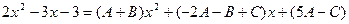Получим: ;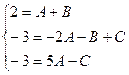

Решая найдем, что, 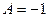,В=3,.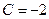

Следовательно, .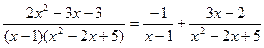

3) интегрирование простейших рациональных дробей

Найдем интегралы от простейших рациональных дробей:

а) 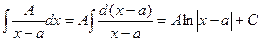(1)

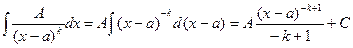б) (2)

в) вычисление интеграла вида

.

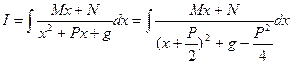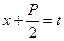, тогда 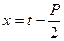и 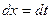. Сделаем подстановку, положим, 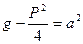. Следовательно, после подстановки получим:

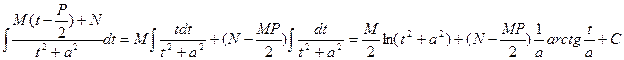и возвращаясь к x, получим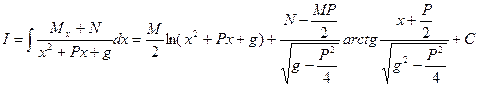

г) Вычисление интеграла вида 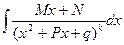, где 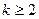,,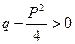 данный интеграл подстановкой 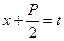сводится к сумме двух интегралов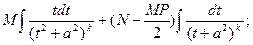 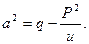Первый интеграл легко вычисляется: 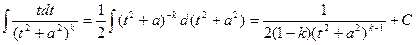. Вычислим второй интеграл: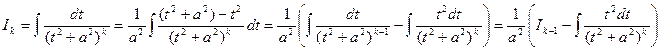

К последнему применим интегрирование по частям. Положим u=t, 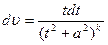, 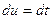; 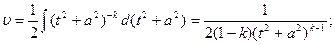тогда 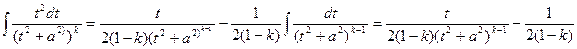I_k-1. Подставляя это значение в выражения для I_k, найдем: 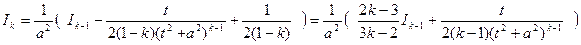. Полученное соотношение дает возможность найти I_k для любого натурального числа х>1.

д) интегрирование рациональных дробей

Рассмотренный выше материал позволяет сформулировать основные правила интегрирования рациональных дробей.

1) если дробь неправильна, то представить ее в виде суммы многочлена и правильной дроби.

2) Разложив знаменатель правильной рациональной дроби на множители, представить ее в виде суммы простейших рациональных дробей.

3) Проинтегрировать многочлен и полученную сумму простейших дробей.

Пример:

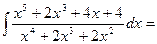(проделав операции пунктов 1) и 2), получим)

=.

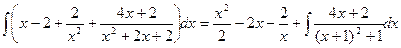Последний интеграл берем методом подстановки x+1=t, тогда x=t-1 и dx=dt. Таким образом, 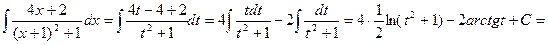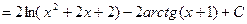. Следовательно,

.

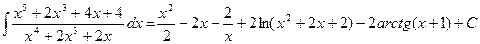Дата добавления: 2013-12-12