
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вычисление тройного интеграла
|
|
|
|
Тройной интеграл. Основные понятия
Обобщением определенного интеграла на случай функции трех переменных является так называемый тройной интеграл. Теория тройного интеграла аналогична теории двойного интеграла, поэтому изложим ее в сокращенном виде.
Пусть в замкнутой области V пространства oxyz задана непрерывная функция 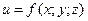 . Разбив область V сеткой поверхностей на n частей
. Разбив область V сеткой поверхностей на n частей 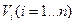 и выбрав в каждой их них произвольную точку
и выбрав в каждой их них произвольную точку 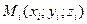 составим интегральную сумму
составим интегральную сумму 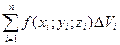 для функции
для функции 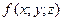 по области V (∆Vi – объем элементарной области Vi). Если предел интегральной суммы существует при неограниченном увеличении числа n таким образом, что каждая Vi стягивается в точку, то его называют тройным интегралом от функции
по области V (∆Vi – объем элементарной области Vi). Если предел интегральной суммы существует при неограниченном увеличении числа n таким образом, что каждая Vi стягивается в точку, то его называют тройным интегралом от функции 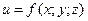 по области V и обозначают
по области V и обозначают 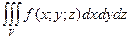 (или
(или 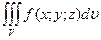 ). Таким образом, по определению получаем
). Таким образом, по определению получаем 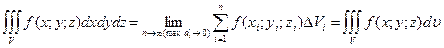 . Здесь
. Здесь 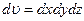 - элемент объема
- элемент объема 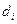 - диаметр i-области.
- диаметр i-области.
Теорема. Если функция 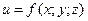 непрерывна в ограниченной замкнутой области V, то предел интегральной суммы при
непрерывна в ограниченной замкнутой области V, то предел интегральной суммы при 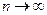 b
b 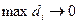 существует и не зависит ни от способа разбиения области V на части, ни от выбора точек
существует и не зависит ни от способа разбиения области V на части, ни от выбора точек 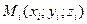 в них.
в них.
Тройной интеграл обладает теми же свойствами, что и двойной:
1) 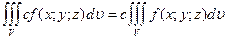 , где
, где 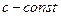 .
.
2) 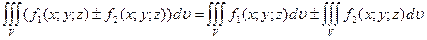 .
.
3) 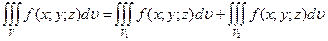 , если
, если 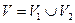 , а пересечение V1 и V2 состоит из границы, их разделяющей.
, а пересечение V1 и V2 состоит из границы, их разделяющей.
4) 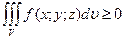 , если в V
, если в V  . Если же в V
. Если же в V 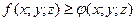 , то и
, то и 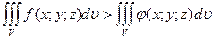 .
.
5) 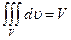 , так как в случае
, так как в случае 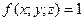 любая интегральная сумма имеет вид
любая интегральная сумма имеет вид 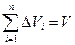 и численно равна объему тела.
и численно равна объему тела.
6) Оценка тройного интеграла
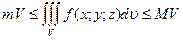 , где m и M – соответственно наименьшее и наибольшее значение функции
, где m и M – соответственно наименьшее и наибольшее значение функции 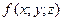 в области V.
в области V.
7) Теорема о среднем значении
Если функция 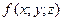 непрерывна в замкнутой области V, то в этой области существует такая точка
непрерывна в замкнутой области V, то в этой области существует такая точка 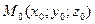 , что
, что 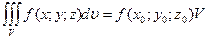 , где V – объем тела.
, где V – объем тела.
Вычисление тройного интеграла сводится к последовательному вычислению трех определенных интегралов. Пусть областью интегрирования является тело, ограниченное снизу поверхностью 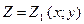 , сверху поверхностью
, сверху поверхностью 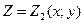 , причем
, причем 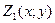 и
и 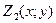 (
(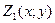 ≤
≤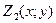 ) – непрерывные функции в замкнутой области
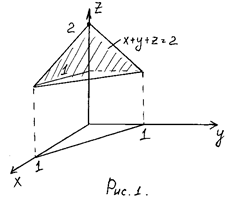
) – непрерывные функции в замкнутой области 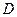 , являющейся проекцией тела на плоскость оху (рис.1). Будем считать область V правильной в направлении оси oz. Любая прямая, параллельная оси oz, пересекает границу области не более, чем в двух точках. Тогда для любой непрерывной в области V функции
, являющейся проекцией тела на плоскость оху (рис.1). Будем считать область V правильной в направлении оси oz. Любая прямая, параллельная оси oz, пересекает границу области не более, чем в двух точках. Тогда для любой непрерывной в области V функции 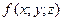 имеет место соотношение
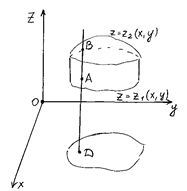
имеет место соотношение 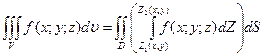 , сводящее вычисление тройного интеграла к вычислению двойного интеграла от однократного (доказательство этого соотношения мы упускаем). При этом сначала вычисляется внутренний интеграл по переменной Z при постоянных х и у в пределах изменения Z. Нижней границей интеграла является аппликата точки АК – точки входа прямой, параллельной оси oz, в область V, т.е.
, сводящее вычисление тройного интеграла к вычислению двойного интеграла от однократного (доказательство этого соотношения мы упускаем). При этом сначала вычисляется внутренний интеграл по переменной Z при постоянных х и у в пределах изменения Z. Нижней границей интеграла является аппликата точки АК – точки входа прямой, параллельной оси oz, в область V, т.е. 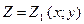 , верхней границей аппликата точки В – точки выхода прямой из области V, т.е.
, верхней границей аппликата точки В – точки выхода прямой из области V, т.е. 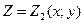 . Результат вычисления этого интеграла есть функция двух переменных х и у. Если область
. Результат вычисления этого интеграла есть функция двух переменных х и у. Если область 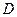 ограничена линиями
ограничена линиями 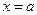 ,
, 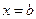 (a<b),
(a<b), 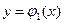 и
и 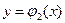 , где
, где 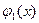 и
и 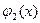 - непрерывные на отрезке
- непрерывные на отрезке 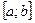 функции, причем
функции, причем 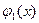 ≤
≤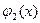 (рис.2), то, переходя от тройного интеграла к повторному получаем формулу:
(рис.2), то, переходя от тройного интеграла к повторному получаем формулу: 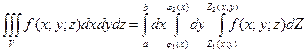 . С помощью этого соотношения и производятся вычисления тройных интегралов.
. С помощью этого соотношения и производятся вычисления тройных интегралов.
 Пример. Вычислить
Пример. Вычислить 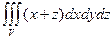 , где V ограничивается плоскостями
, где V ограничивается плоскостями 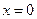 ,
, 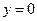 ,
, 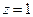 и
и 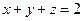 (рис.1). Область V является правильной в направлении оси oz (как в направлении ох и оу). Ее проекция на плоскость оху является правильной в направлении оу и ох. Поэтому, применяя выше полученное соотношению имеем
(рис.1). Область V является правильной в направлении оси oz (как в направлении ох и оу). Ее проекция на плоскость оху является правильной в направлении оу и ох. Поэтому, применяя выше полученное соотношению имеем 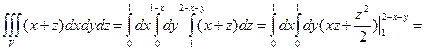
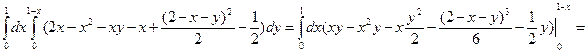

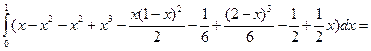
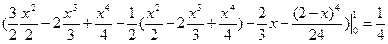 .
.
|
|
|
|
|
Дата добавления: 2013-12-12; Просмотров: 561; Нарушение авторских прав?; Мы поможем в написании вашей работы!