Признак Лейбница

Знакочередующиеся и знакопеременные ряды

Рассмотрим важный класс рядов, называемых знакочередующимися. Такими рядами называется ряд вида: 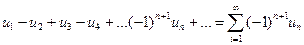, где 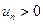для всех . Для знакочередующихся рядов имеет место достаточный признак сходимости (Признак Лейбница).

Теорема Лейбница. Знакочередующийся ряд сходится, если:

1) последовательность абсолютных величин членов ряда монотонно убывает, т.е.

2) общий член ряда стремится к нулю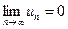. При этом сумма 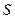ряда удовлетворяет неравенствам .

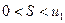Доказательство:

Рассмотрим сначала частичную сумму четного числа 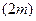членов ряда. Имеем 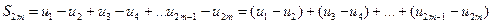. Выражения в каждой скобке согласно первому условию теоремы положительно. Следовательно, сумма 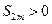и возрастает с возрастанием номера .

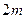С другой стороны 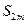, можно переписать так: 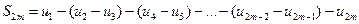. Легко увидеть, что 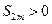. Таким образом, последовательность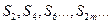возрастает и ограничена сверху. Следовательно, она имеет предел 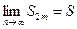, причем .

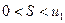Рассмотрим теперь частичные суммы нечетного числа 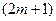членов ряда. Очевидно, что 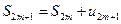. Отсюда следует, что 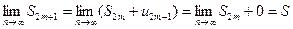. Т.к. 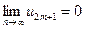в силу второго условия теоремы. Итак, 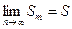как при четном 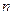, так и при нечетном 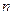. Следовательно, наш ряд сходится, причем .

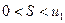Замечания.

1) Исследование знакочередующихся рядов вида 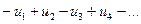(с отрицательным первым членом) сводится путем умножения всех его членов на (-1) к исследованию ряда с + первым членом.

2) Соотношение 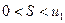позволяет получить простую и удобную оценку ошибки, которую мы допускаем, заменяя сумму 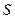данного ряда его частичной суммой 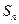. Отброшенный ряд представляет собой также знакочередующийся ряд, сумма которого по модулю меньше первого члена этого ряда, т.е. 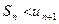поэтому ошибка меньше модуля первого из отброшенных членов.

Пример.

Вычислить сумму ряда 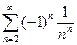. Данный ряд лейбницевского вида. Он сходится. Можно записать 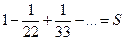. Взяв 5 членов, т.е. заменив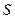на 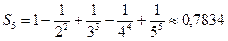сделаем ошибку, меньшую чем 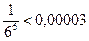. Итак, .

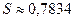Дата добавления: 2013-12-12