Равномерное прямолинейное движение

Введение. Кинематика

Механика

Механика изучает механическое движение, условия и причины, вызывающие данное движение, а также условия равновесия тел. Механическим движением называется изменение положения тела или его частей относительно других тел с течением времени. Всякое движение относительно. Характер движения зависит от того, относительно каких тел мы рассматриваем данное движение.

Тело, относительно которого мы рассматриваем положение других тел в пространстве, называется телом отсчета.

Системой отсчета называют систему координат, связанную с телом отсчета, и выбранный метод отсчета времени, т.е. часы.

Выбор системы отсчета зависит от условий данной задачи. Движение реальных тел, как правило, сложное. Поэтому для упрощения рассмотрения движений пользуются законом независимости движений: всякое сложное движение можно представить как сумму независимых простейших движений. К простейшим движениям относятся поступательное и вращательное.

В физике широко пользуются моделями, которые позволяют из всего многообразия физических свойств выбрать главное, определяющее данное физическое явление. Одними из первых моделей реальных тел являются материальная точка и абсолютно твердое тело.

Материальной точкой называется тело, размерами которого можно пренебречь в условиях данной задачи. Абсолютно твердым телом называется тело, расстояние между любыми двумя точками которого остается постоянным при его движении.

Эти модели позволяют исключить деформацию тел при движении.

Поступательным называется движение, при котором отрезок, соединяющий любые две точки твердого тела, перемещается при движении параллельно самому себе. Из этого следует, что все точки тела при поступательном движении движутся одинаково, т.е. с одинаковыми скоростями и ускорениями. Примером поступательного движения может служить движение кабины "чертова колеса".

Вращательным называется движение, при котором все точки абсолютно твердого тела движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения, причем эти окружности лежат в плоскостях, перпендикулярных оси вращения.

Пользуясь законом независимости движений, сложное движение твердого тела можно рассматривать как сумму поступательного и вращательного движений.

Одним из первых разделов механики является кинематика, изучающая механическое движение тел без выяснения причин, вызывающих данное движение.

Можно воспользоваться понятием материальной точки для изучения поступательного движения абсолютно твердого тела, так как все точки движутся одинаково. Для определения положения материальной точки в пространстве и описания ее движения необходимы следующие понятия.

Перемещение ∆s - вектор, соединяющий начальную и конечную точки траектории, по которой двигалась материальная точка некоторый промежуток времени.

Траектория – линия, описываемая при движении материальной точкой в пространстве.

Путь ℓ - сумма длин отрезков траектории.

При прямолинейном движении (траектория – прямая линия) модуль перемещения равен длине пути ℓ, если движение происходит в одном направлении.

Быстрота изменения положения материальной точки в пространстве с течением времени характеризуется средней и мгновенной скоростями.

Средняя скорость – векторная величина, равная отношению перемещения к промежутку времени, за которое это перемещение произошло:

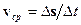. (1.1)

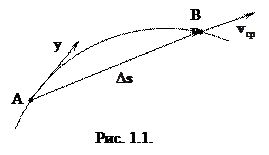Пусть точка движется по траектории от А до В. На рис. 1.1 показаны перемещение ∆s и вектор средней скорости v _ср.

Часто для характеристики движения вводится средняя скорость прохождения пути, равная отношению пути к промежутку времени, за который этот путь пройден:

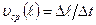(1.2)

На рис. 1.1 ∆ℓ - это длина дуги АВ. Ясно, что, поскольку 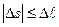, то | v _ср| ≤ υ_ср(ℓ)‌‌. Скорость в данный момент времени определяется мгновенной скоростью.

Мгновенной скоростью называется предел отношения перемещения ∆s к промежутку времени ∆t, за который это перемещение произошло, при стремлении ∆t к нулю:

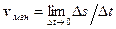(1.3)

Мгновенная скорость направлена по касательной к траектории. Это вытекает из следующих соображений: v_ср направлено вдоль секущей АВ (рис. 1.1). Если ∆t стремиться к нулю, то в пределе точки А и В сольются в одну точку, при этом секущая превращается в касательную.

Равномерным прямолинейным называется движение, при котором материальная точка за любые равные промежутки времени совершает одинаковые перемещения. При этом движении мгновенная скорость совпадает со средней:

.

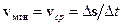Если выбрать ось х вдоль направления движения, то проекция скорости на ось х равна величине скорости:

.

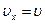Из определения скорости следует

,

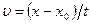Откуда закон движения материальной точки, т.е. 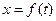, имеет вид

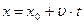, (1.4)

Где х₀ – координата материальной точки в момент времени t = 0. Если скорость направлена в сторону, противоположную положительному направлению оси х, то

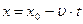. (1.5)

На рис. 1.2 показаны зависимост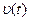и и 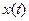от времени.

Дата добавления: 2013-12-12