Газовые законы

Молекулярная физика и термодинамика

Следствия уравнения Бернулли

1. Закон Бернулли: Если жидкость течет по горизонтальному каналу, то, чем больше скорость течения жидкости, тем меньше давление.

2. Формула Торичелли. Если в сосуде есть отверстие, через которое течет жидкость (рис. 7.10), то, записывая уравнение Бернулли для сечений 1 - 1' и 2 - 2', получим

.

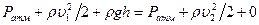Так как 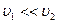, для скорости струи, вытекающей из отверстия, имеем

.

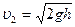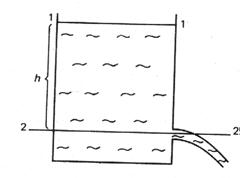
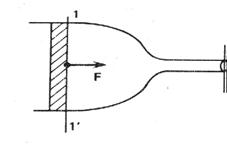
Рис. 7.10. Рис. 7.11.

3. Пусть имеется трубка переменного сечения (рис. 7.11), в одном из сечений находится поршень, на который давят с силой F. Если площадь сечения 1 - 1' есть 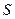, то давление жидкости в этом сечении равно 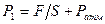. Тогда уравнение Бернулли запишется в виде

.

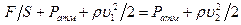Все тела состоят из молекул. Молекулярная физика, изучая поведение молекул, объясняет состояние системы и процессы, протекающие в системе. Молекулы находятся в непрерывном движении. Хаотическое движение молекул обычно называется тепловым движением. Интенсивность теплового движения возрастает с увеличением температуры.

Молекулы взаимодействуют друг с другом. Между ними действуют силы притяжения и силы отталкивания, которые быстро убывают при увеличении расстояния между молекулами. Силы отталкивания действуют только на очень малых расстояниях. Практически поведение вещества и его агрегатное состояние определяются тем, что является доминирующим: силы притяжения или хаотическое тепловое движение. В твердых телах, где концентрация молекул 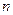(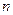- число молекул в единице объема) относительно велика, доминируют силы взаимодействия, и твердое тело сохраняет свои размеры и форму. Жидкости, где концентрация меньше, а следовательно, меньше силы взаимодействия, сохраняют свой объем, но принимают форму сосуда, в котором они находятся. В газах, где концентрация молекул еще меньше, силы взаимодействия малы, поэтому газ занимает весь предоставленный ему объем.

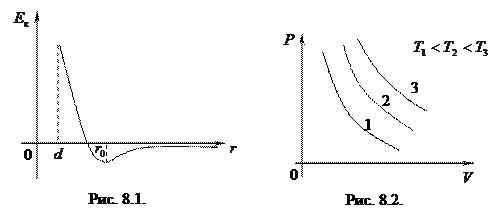На рис. 8.1 приведен график зависимости потенциальной энергии взаимодействия двух молекул от расстояния между ними. Пусть в точке 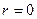находится молекула и вторая молекула приближается к ней из бесконечности.

Напомним, что 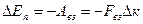, откуда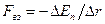

При 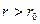сила притяжения больше, чем сила отталкивания: 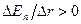. При 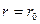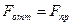, потенциальная энергия минимальна, суммарная сила, действующая на молекулы, равна нулю. При 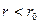сила отталкивания становится больше силы притяжения: 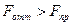(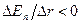). При значениях 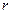~ 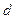потенциальная энергия стремится к бесконечности. Это означает, что сила отталкивания также стремится к бесконечности, т. е. две молекулы не могут приблизиться друг к другу на расстояние меньше, чем 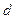. Это позволило рассматривать молекулы как два упругих шарика диаметрами 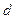, так как 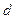- минимальное расстояние между их центрами. Взаимодействие молекул рассматривается по законам абсолютно упругого удара (модель реального взаимодействия).

Силы, действующие между молекулами газа, малы и поэтому часто ими можно пренебречь. Кроме того, можно пренебречь объемом, который занимают молекулы. Газ, для которого это справедливо, называется идеальным газом. Любой газ при давлениях, меньших 10 атм, можно рассматривать как идеальный. Газ характеризуется тремя параметрами: объемом V, давлением Р и температурой Т. Температура может быть измерена по разным температурным шкалам. Абсолютная температура связана с температурой по шкале Цельсия соотношением: 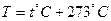, изменение температуры по шкале Кельвина равно изменению температуры по шкале Цельсия: .

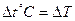Если значения температуры и давления в различных точках объема разные, то температура и давление являются функциями координат, т. е. 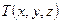, 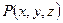. В этом случае газ (система) находится в неравновесном состоянии, и мы не можем назвать значения давления и температуры, определяющие состояние системы. Если систему, находящуюся в неравновесном состоянии, предоставить самой себе, то температура и давление постепенно выравниваются, система приходит в равновесное состояние. Процесс перехода к равновесному состоянию называется релаксацией, а время, необходимое для этого, временем релаксации. Равновесное состояние — это состояние, при котором температура и давление во всех точках объема одинаковы. Состояние газа может быть определено, если он находится в равновесном состоянии.

На графиках зависимости 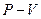, , 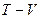мы можем изображать только процессы, при которых каждое промежуточное состояние является равновесным. Такие процессы называются обратимыми. Экспериментально исследовались процессы, при которых один из трех параметров и масса газа оставались неизменными. Эти законы называются газовыми законами, и если газ подчиняется газовым законам, его можно считать идеальным (еще одно определение идеального газа).

1. Закон Бойля — Мариотта. Для данной массы газа при постоянной температуре произведение давления на объем остается величиной постоянной:

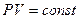. (8.1)

Зависимость давления от объема изображена на рис. 8.2.

Процессы, происходящие при постоянной температуре, называются изотермическими, а кривые, изображающие процессы при 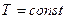, называются изотермами. Поскольку 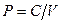(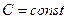), изотермы являются гиперболами.

2. Закон Гей-Люссака. Для данной массы газа при постоянном давлении объем изменяется при увеличении температуры по линейному закону:

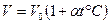, (8.2)

где 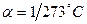. Подставив 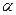в (8.2), получим

.

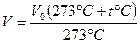Введем абсолютную температуру 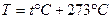, откуда

.

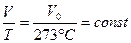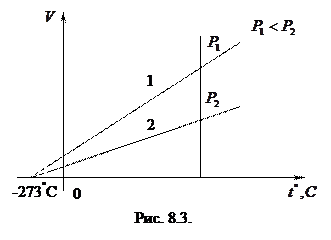Закон Гей-Люссака можно сформулировать следующим образом: отношение объема к абсолютной температуре для данной массы газа при постоянном давлении остается постоянным. Процессы, происходящие при постоянном давлении, называются изобарными, а кривые, изображающие изобарный процесс, изобарами. На рис. 8.3 показаны две изобары при различных давлениях 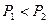(очевидно, что при данной температуре, чем больше объем, тем меньше давление). Около точки 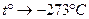(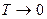) зависимости изображены пунктирными линиями. Это понятно, так как при низких температурах газ превращается в жидкость и законы, найденные экспериментально для газа, не работают. Продолжив экспериментальные зависимости 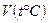до пересечения с осью абсцисс, найдем, что они пересекаются в одной точке .

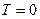3. Закон Шарля. Для постоянной массы газа при постоянном объеме отношение давления газа к его температуре остается постоянным:

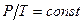при ,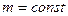

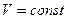
Процессы, происходящие при постоянном объеме, называются изохорными, и кривые их изображающие — изохорами.

На рис. 8.4 изображены изохорные процессы при разных значениях объема. Зависимости вблизи абсолютного нуля изображены так же, как и при изобарных процессах, пунктирными линиями. Указанные три закона устанавливают связь двух из трех параметров газа.

Уравнение, устанавливающее связь всех трех параметров при постоянной массе ram, называется объединенным газовым законом.

Пусть система, находящаяся в состоянии 1 (рис. 8.5), характеризующемся параметрами 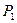, , 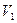, 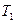перешла и состояние 2, характеризующееся параметрами 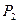, , 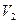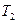. Переведем систему из состояния 1 и 2 следующим образом: сначала газ изотермически расширяется до объема 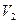(кривая 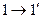), а затем изохорно нагревается до температуры 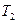(отрезок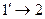). Итак, промежуточное состояние газа 1' характеризуется параметрами , , .

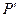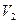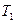При изотермическом расширении справедливо выражение

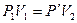(8.3)

(закон Бойля - Мариотта). При изохорном нагревании

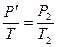(8.4)

(закон Шарля). Выразив 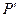из (8.3) и (8.4) и приравняв выражение для 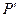, получим

,

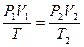т.е при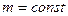

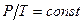. (8.5)

Уравнение Клапейрона — Менделеева, или уравнение состояния идеального газа, связывает термодинамические параметры и массу газа.

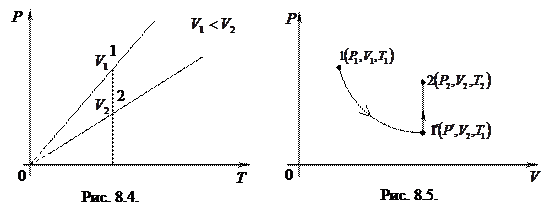Моль равен количеству вещества, содержащему столько же молекул, сколько их содержит 0,012 кг углерода (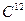). В одном моле любого вещества число
молекул равно числу Авогадро

.

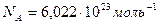Мacca моля М равна произведению массы одной молекулы 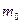на число Авогадро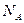

.

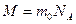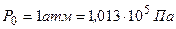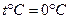Известно, что 1 моль любого газа при нормальных условиях (и или 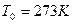) занимает объем 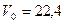л. Для одного моля можно записать уравнение (8.5):

.

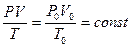Величина 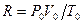называется универсальной (одинаковой для всех газов) газовой постоянной:

.

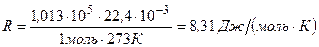Итак, 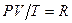, или 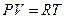. Если в объеме 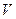содержится 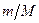молей, то

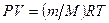(8.6)

- уравнение Клапейрона – Менделеева. Все выше перечисленные газовые законы являются частным случаем уравнения Клапейрона – Менделеева. Газовая постоянная 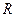связана с числом Авогадро и постоянной Больцмана :

,

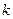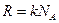где 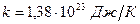. Подставив это выражение в (8.6), получим 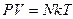, где 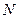- число молекул газа. Величина 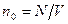называется концентрацией молекул. Таким образом,

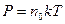. (8.7)

Уравнения (8.6) и (8.7) называются уравнениями состояния идеального газа.

Если в сосуде объемом 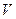находится смесь газов, то давление смеси определяется законом Дальтона:давление смеси газов равно сумме парциальных давлений: 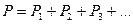. Парциальное давление – это давление компонентов смеси, если бы она занимала весь объем, т.е.

,

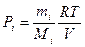где 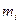и 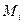- масса и масса моля i –ой компоненты смеси соответственно. Итак, если в сосуде находится смесь газов, состоящая из 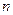компонентов, то

.

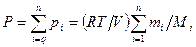Так как 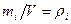- плотность i –ой компоненты.

.

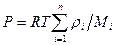Атмосферное давление также определяется суммой парциальных давлений компонентов, из которых состоит воздух: кислорода, углекислого газа, азота, паров воды:

,

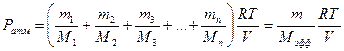где 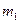, , 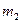, 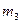…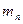и 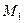, , 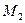, 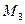…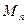- массы и массы молей кислорода, углекислого газа, азота, паров воды в объеме 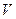, 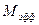- эффективная масса моля воздуха, 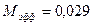кг/моль.

Дата добавления: 2013-12-12