Системы линейных уравнений общего вида

Если система (5.1) оказалась совместной, т. е. матрицы A и 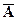имеют один и тот же ранг, то могут представиться две возможности ‑ a) 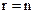, б) :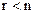

а) если 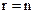, то имеем n независимых уравнений с n неизвестными, причем определитель D этой системы отличен от нуля. Такая система имеет единственное решение, получаемое по формулам Крамера;

б) если 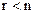, то число независимых уравнений меньше числа неизвестных.

Перенесем лишние неизвестные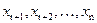, которые принято называть свободными, в правые части; наша система линейных уравнений примет вид:

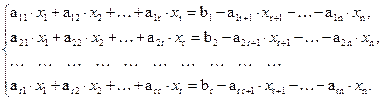
Ее можно решить относительно x₁, x₂,..., x_r, так как определитель этой системы (r-го порядка) отличен от нуля. Придавая свободным неизвестным произвольные числовые значения, получим по формулам Крамера соответствующие числовые значения для x₁, x₂,..., x_r. Таким образом, при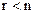имеем бесчисленное множество решений.

Система (5.1) называется однородной, если все b_i = 0, т. е. она имеет вид:

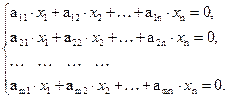(5.5)

Из теоремы Кронекера-Капелли следует, что она всегда совместна, так как добавление столбца из нулей не может повысить ранга матрицы. Это, впрочем, видно и непосредственно - система (5.5) заведомо обладает нулевым, или тривиальным, решением 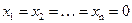. Пусть матрица А системы (5.5) имеет ранг r.

Если 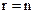, то нулевое решение будет единственным решением системы (5.5); при 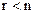система обладает решениями, отличными от нулевого, и для их разыскания применяют тот же прием, как и в случае произвольной системы уравнений.

Всякий ненулевой вектор ‑ столбец 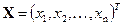называется собственным вектором линейного преобразования (квадратной матрицы A), если найдется такое число l, что будет выполняться равенство .

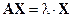Число 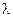называется собственным значением линейного преобразования (матрицы A), соответствующим вектору X. Матрица A имеет порядок n.

Для нахождения собственных значений матрицы A перепишем равенство 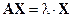в виде 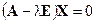, где E - единичная матрица n-го порядка или в координатной форме:

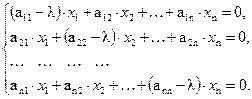(5.6)

Получили систему линейных однородных уравнений, которая имеет ненулевые решения тогда и только тогда, когда определитель этой системы равен нулю, т.е.

.

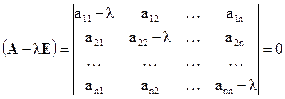Получили уравнение n-ой степени относительно неизвестной l, которое называется характеристическим уравнением матрицы A, многочлен 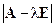называется характеристическим многочленом матрицы A, а его корни - характеристическими числами, или собственными значениями, матрицы A.

Для нахождения собственных векторов матрицы A в векторное уравнение 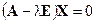или в соответствующую систему однородных уравнений (5.6) нужно подставить найденные значения l и решать обычным образом.

Пример 2.16. Исследовать систему уравнений и решить ее, если она совместна.

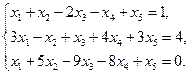
Решение. Будем находить ранги матриц A и 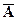методом элементарных преобразований, приводя одновременно систему к ступенчатому виду:

.

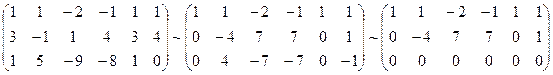Очевидно, что 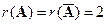. Исходная система равносильна следующей, приведенной к ступенчатому виду:

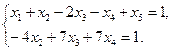
Поскольку определитель при неизвестных x ₁ и x ₂ отличен от нуля, то их можно принять в качестве главных и переписать систему в виде:

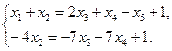
откуда 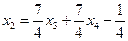, 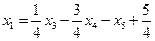‑ общее решение системы, имеющей бесчисленное множество решений. Придавая свободным неизвестным x ₃, x ₄, x ₅ конкретные числовые значения, будем получать частные решения. Например, при 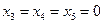, , 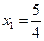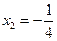. Вектор 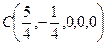является частным решением данной системы.

Пример 2.17. Исследовать систему уравнений и найти общее решение в зависимости от значения параметра а.

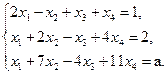
Решение. Данной системе соответствует матрица 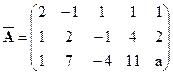. Имеем 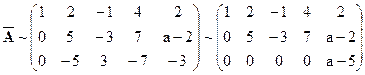следовательно, исходная система равносильна такой:

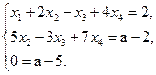
Отсюда видно, что система совместна только при a=5. Общее решение в этом случае имеет вид:, _.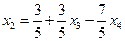

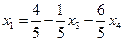Пример 2.18. Выяснить, будет ли линейно зависимой система векторов:

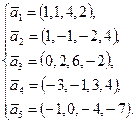
Решение. Система векторов является линейно зависимой, если найдутся такие числа x ₁, x ₂, x ₃, x ₄, x ₅, из которых хотя бы одно отлично от нуля (см. п. 1. разд. I), что выполняется векторное равенство:

.

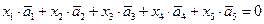В координатной записи оно равносильно системе уравнений:

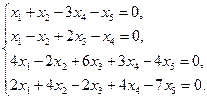
Итак, получили систему линейных однородных уравнений. Решаем ее методом исключения неизвестных:

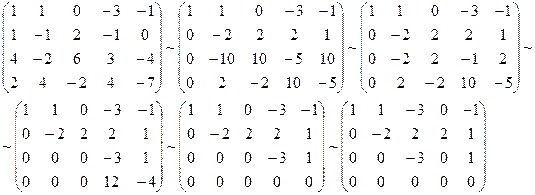
Система приведена к ступенчатому виду, ранг матрицы равен 3, значит, однородная система уравнений имеет решения, отличные от нулевого 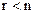. Определитель при неизвестных x ₁, x ₂, x ₄ отличен от нуля, поэтому их можно выбрать в качестве главных и переписать систему в виде:

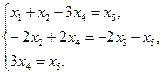
Имеем: , , .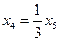

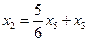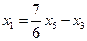Система имеет бесконечное множество решений; если свободные неизвестные x₃ и x₅ не равны нулю одновременно, то и главные неизвестные отличны от нуля. Следовательно, векторное уравнение

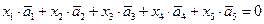
имеет коэффициенты, не равные нулю одновременно; пусть например, 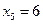, 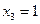. Тогда 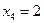, , 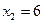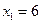и мы получим соотношение

,

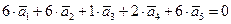т.е. данная система векторов линейно независима.

Пример 2.19. Найти собственные значения и собственные векторы матрицы

.

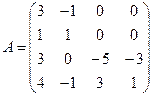Решение. Вычислим определитель матрицы A

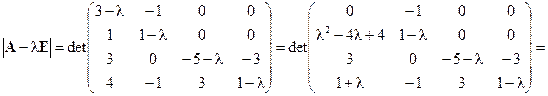
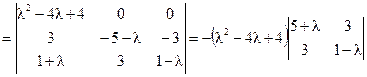
Итак, 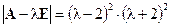. Корни характеристического уравнения 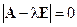‑ это числа l₁ = 2 и l₂ = ‑2. Другими словами, мы нашли собственные значения матрицы A. Для нахождения собственных векторов матрицы A подставим найденные значения l в систему (5.6): при l = 2 имеем систему линейных однородных уравнений

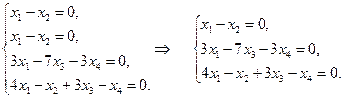
Следовательно, собственному значению l = 2 отвечают собственные векторы вида a (8, 8, -3, 15), где a - любое отличное от нуля действительное число. При l = -2 имеем:

,

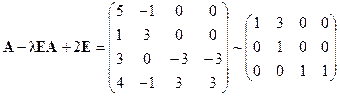и поэтому координаты собственных векторов должны удовлетворять системе уравнений

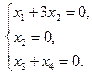
Поэтому собственному значению l = -2 отвечают собственные векторы вида b (0, 0,-1, 1), где b - любое отличное от нуля действительное число.

Дата добавления: 2013-12-12