Степень свободы и расчетная модель колебательной системы

Введение в динамику сооружений

ДИНАМИКА СООРУЖЕНИЙ

Колебания представляют одну из наиболее распространенных форм движения. Колеблются ветви деревьев, зажатая в тисках металлическая пластинка, колеблются качели, вагоны на рессорах при движении, вода и предметы на ней. Колеблются здания и сооружения от ветра, землетрясения, от работы различных машин и механизмов. При колебании сооружения величины и знаки внутренних усилий (напряжений) непрерывно меняются, что может привести к быстрому разрушению отдельных элементов, частей или всего сооружения.

Динамика сооружений изучает механические колебания сооружений. Как теоретическая наука, она разрабатывает различные методы и алгоритмы расчета сооружений на динамические воздействия. В то же время она является прикладной наукой и решает конкретные задачи. Среди решаемых динамикой сооружений задач самыми важными являются четыре задачи динамики:

1) определение частот и форм собственных колебаний;

2) проверка на резонанс;

3) проверка динамической прочности;

4) проверка динамической жесткости.

Решение задач динамики намного сложнее решения задач статики, т.к. приходится учитывать дополнительный фактор – время.

При расчете на колебания сооружение рассматривается как колебательная система. Колебательные системы делятся на два типа. Диссипативная система – это система, у которой происходит диссипация (рассеивание) энергии. Консервативная система – это система, у которой рассеиванием энергии пренебрегают.

Простейшей моделью консервативной колебательной системы является система из пружины и одной массы (рис. 16.1 а). Жесткость пружины r характеризует упругость системы, а масса m – ее инерционные свойства.

Простейшей моделью диссипативной системы является система из пружины, вязкого элемента и массы (рис. 16.2). Сила сопротивления c, возникающая в вязком элементе, стремится остановить колебания системы. Такой элемент называют демпфером (или амортизатором). Поэтому диссипативную систему часто называют демпфированной системой.

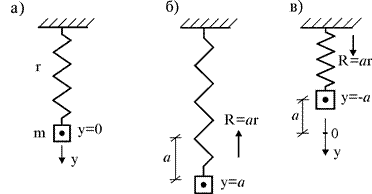
Рис. 16.1 Рис. 16.2

Под степенью свободы в динамике сооружений понимается направление возможного независимого перемещения отдельной массы. В отличие от понятия степени свободы в кинематическом анализе, при определении динамических степеней свободы учитываются и деформации элементов.

Число динамических степеней свободы W_дин – это наименьшее число параметров, необходимых для определения положения всех масс системы.

Если рассматривать сооружение как систему из бесконечного числа элементарных масс, получим систему с бесконечным числом динамических степеней свободы. Расчет колебаний даже простейших систем (балок, плит или оболочек) по такой континуальной модели является непростой задачей. Поэтому в динамике сооружений расчетная модель выбирается в виде системы с сосредоточенными массами.

Массы сооружения можно дискретизировать по-разному. Иногда, сосредоточив распределенную массу сооружения только в нескольких точках, можно достаточно точно рассчитать простейшие колебания.

Массу сооружения обычно сосредотачивают в характерных точках, где действуют наибольшие нагрузки. Если положение таких точек установить трудно, места и величины сосредоточенных масс могут быть найдены из условия равенства энергий всей системы и ее дискретной модели. Сосредоточенные массы, определяемые таким способом, называются приведенными массами. Большие массы, сосредоточенные на сооружении (грузы, различные машины, станки, оборудование и др.) рассматриваются как кусковые массы.

Приведенные и кусковые массы плоской системы имеют три степени свободы: они могут совершать колебания в двух независимых взаимно-перпендикулярных направлениях и вращаться относительно центра массы. Если вращение (крутильное колебание) массы не учитывать, получим точечную массу. Число степеней свободы точечной массы равно двум.

Рассмотрим ряд примеров.

1. Шарнирно-опертая балка (рис. 16.3 а) состоит из бесконечного числа элементарных масс dm, положение которых определяют бесконечное число перемещений y(x). Поэтому W_дин =∞. Если же массу балки сосредоточить в одной точке, положение точечной массы m будет определять один параметр – перемещение y_m (рис. 16.3 б). Тогда W_дин = 1. Если массу балки сосредоточить в трех точках, то по-

Рис. 16.3 ложение масс m₁, m₂, m₃ будут определять три параметра y₁, y₂, y₃ (рис. 16.3 в). Поэтому у этой системы W_дин = 3.

2. Водонапорная башня (рис. 16.4 а) и одноэтажная рама (рис. 16.4 в). У них основные массы расположены наверху. Поэтому их можно рассматривать как колебательные системы с одной массой и одной степенью свободы, т.е. принять W_дин = 1 (рис. 16.4 б, г).

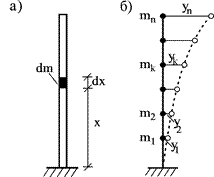Рис. 16.3

3. Дымовую трубу с распределенной массой (рис. 16.5 а) нельзя рассматривать как динамическую систему только с одной степенью свободы, так как это приводит к неточным результатам. Ее следует рассматривать как систему с достаточно большим числом степеней свободы (рис. 16.5 б) и принять W_дин = n.

Рис. 16.5

Дата добавления: 2013-12-12