Явления, наблюдаемые при попадании света в дисперсные

ГЛАВА 8

Рис. 7.4. Седиментационная кривая полидисперсной суспензии

Рис. 7.2. Седиментационная кривая монодисперсной суспензии

Если m_¥ - общая масса дисперсной фазы, h – первоначальная высота столба суспензии, то m_¥/ h – масса дисперсной фазы в объёме, приходящемся на единицу длины столба суспензии. При скорости осаждения частиц v в течение произвольного времени t < t_¥ вещество осядет из столба высотой vt, а масса осадка, накопившаяся за это время, выразится уравнением

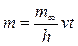
Так как величины m_¥, h и v постоянны, то масса частиц, осевших из монодисперсной суспензии, прямо пропорциональна времени седиментации, что и отражается линейным участком ОВ на рис. 7.2. Подставляя значение скорости оседания из уравнения Стокса, получим

,

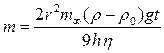откуда можно рассчитать радиус частиц

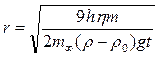
и удельную поверхность суспензии по массе

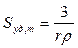
и по объёму

.

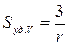В отличие от монодисперсных в полидисперсных системах частицы оседают с различными скоростями, поскольку имеют разные размеры. Если система достаточно разбавлена и её частицы движутся независимо друг от друга, можно представить, что в одном объёме одновременно происходит оседание нескольких монодисперсных суспензий. Ход седиментации каждой из них будет выражаться графиками, аналогичными рис. 7.2. Причём, чем меньше диаметр частиц, тем более пологой будет участок ОВ и тем больше время полного оседания всех одинаковых частиц.

Седиментационная кривая бидисперсной суспензии (рис. 7.3) получается геометрическим сложением двух кривых, принадлежащих более крупным и более мелким частицам.

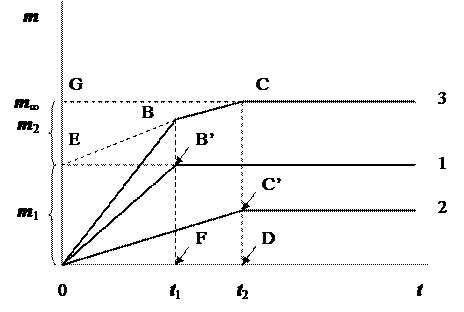Рис. 7.3. Седиментационная кривая бидисперсной суспензии

1 – кривая для суспензии с крупными частицами;

2 – кривая для суспензии с мелкими частицами

3 – суммарная кривая

Из сравнения рис. 7.2 и рис. 7.3 следует, что отрезки FB’ и DC’ соответствуют массам частиц крупной и мелкой фракций, а отрезки DC и 0G – суммарной массе m_¥ осадка, состоящего из крупных и мелких частиц, и образовавшегося после полного оседания суспензии (время t ₂). Продлим линию ВС до пересечения с осью ординат (точка Е). Видно, что при этом образуются два отрезка, причём 0Е соответствует массе крупных частиц m ₁ (0Е = FB’), а EG - массе мелких частиц m ₂ (EG = DC’). То есть, исходя из положения излома на суммарной седиментационной кривой, при анализе бидисперсной суспензии можно определить массы частиц каждой фракции, несмотря на то, что они оседают одновременно.

Аналогичная картина будет наблюдаться и при анализе суспензий, содержащих по три, четыре и т. д. фракции частиц. На седиментационной кривой при этом будет проявляться соответственно три, четыре и т. д. излома, по положению которых можно вычислить массу каждой фракции.

В реальных полидисперсных суспензиях имеются частицы всех возможных в данном интервале размеров. Поэтому на седиментационных кривых, получаемых при их анализе, нет изломов, отвечающих оседанию частиц каждого размера, и они представляют собой плавные кривые, аналогичные показанной на рис. 7.4.

Время, после истечения которого прекращается оседание частиц, и при котором кривая становится прямой, параллельной оси абсцисс, обозначено как t_¥. Шкала времени между 0 и t_¥ разделяется исследователем на несколько отрезков, произвольно или в соответствии с заданной методикой исследования (в данном примере – 0 - t ₁, t ₁ - t ₂, t ₂ - t ₃, - t_¥). Из точек на седиментационной кривой, отвечающих этим отрезкам, проводятся касательные до пересечения с осью ординат. При этом ось ординат разделяется на отрезки, пропорциональные массе осевших частиц разных размеров. Первыми за время t ₁ оседают наиболее крупные частицы (их общая масса равна m ₁, затем за время t ₂ - более мелкие (с массой m ₂), за время t ₃ - ещё более мелкие(с массой m ₃) и т. д. Суммарная масса всех частиц, осевших на чашку седиментометра, будет равна m_¥. Зная это, можно по соотношению отрезков, отвечающих массам, вычислить процентное содержание частиц каждой фракции в суспензии.

Деля заранее измеренную глубину погружения чашечки (т. е. высоту столба суспензии) на время оседания каждой фракции, получают скорость седиментации частиц, а затем по уравнению Стокса вычисляется радиус частиц. Следует помнить, что при этом получается среднее значение из радиусов частиц, оседающих за каждый выбранный интервал времени. Чтобы вычислить все возможные радиусы частиц, имеющихся в суспензии, следовало бы выбрать бесконечно большое число временных интервалов, провести соответственно бесконечно большое число касательных и выполнить соответственное количество вычислений. На практике такая точность обычно не требуется и вполне достаточно знать, что в исследуемой суспензии имеется какое-то число фракций, содержащих частицы с размерами, лежащими внутри определённого интервала.

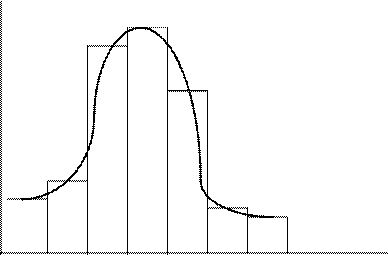
Результаты седиментационного анализа можно наглядно представить в виде гистограммы и/или дифференциальной кривой распределения частиц по фракциям (рис. 7.5).

	m Dr
		r

Рис. 7.5. Гистограмма и дифференциальная кривая распределения

частиц суспензии по фракциям

7.6. Вязкость дисперсных систем

Вязкость дисперсных систем может колебаться в широких пределах. Причём на неё оказывают влияние как размеры частиц дисперсной фазы, так и их концентрация. Чем меньше размеры частиц, тем в меньшей степени проявляется их влияние на вязкость. Коллоидные растворы обладают вязкостью, мало отличающейся от вязкости чистой дисперсионной среды, тогда как суспензии с такой же концентрацией частиц проявляют заметно бóльшую вязкость. С другой стороны, чем больше концентрация частиц, тем больше вязкость. Так, вязкость паст намного больше, чем вязкость суспензий с такими же размерами частиц.

Основы теории вязкости дисперсных систем были заложены А. Эйнштейном. Он исходил из гидродинамических уравнений для микроскопических твёрдых сферических частиц, которые при сдвиге при­обретают дополнительное вращательное движение. Рассеяние энергии при этом является причиной возрастания вязкости. Эйнштейном была установлена связь между вязкостью дисперсной системы h и объёмной долей дисперсной фазы j. Он исходил из того, что относительное приращение вязкости (удельная вязкость)прямо пропорционально относительному содержанию дисперсной фазы (закон Эйнштейна):

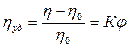
где h ₀ - вязкость дисперсионной среды.

Преобразуя это выражение

, ,

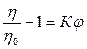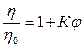получаем в итоге уравнение Эйнштейна:

.

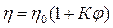Впоследствии Эйнштейн показал, что для сферических частиц коэффициент К равен 5/2 (или 2,5). Тогда можно записать:

.

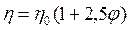Вязкость разбавленных золей мало отличается от вязкости дисперсионной среды. А поскольку объёмная доля дисперсной фаза возрастает с ростом частичной концентрации и с размерами частиц, то вязкость концентрированных золей, а также суспензий и в особенности паст намного больше вязкости дисперсионной среды. А поскольку объёмная доля дисперсной фаза возрастает с ростом частичной концентрации и с размерами частиц, то вязкость концентрированных золей, а также суспензий и в особенности паст намного больше вязкости дисперсионной среды.

7.7. Осмотическое давление дисперсных систем

Т. Грэму при исследовании коллоидных растворов не удалось обнаружить у них осмотического давления. Этот факт он положил в основу деления растворов на коллоидные и истинные. Однако более поздние исследования показали, что и в коллоидных системах можно наблюдать измеримое, хотя и очень малое по величине осмотическое давление.

Для истинных растворов в соответствии с законом Вант-Гоффа осмотическое давление p может быть рассчитано по уравнению

,

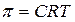где C - молярная концентрация растворённого вещества.

В дисперсных системах концентрацию дисперсной фазы принято выражать числом частиц (мицелл), содержащихся в единице объёма. Эта величина называется численной или частичной концентрацией и обозначается n. Выведем соотношение между молярной концентрацией вещества в растворе и числом частиц, из которых оно состоит. Молярная концентрация представляет собой отношение количества вещества в молях к объёму раствора:

.

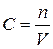Выражая количество молей через число молекул, содержащихся в нём, получим

,

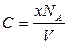а так как x / V = n (n - объёмная концентрация молекул), то

.

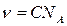Если же под С подразумевается молярная концентрация коллоидных частиц, тогда n - объёмная концентрация этих частиц, или, иначе, частичная концентрация золя.

Поэтому уравнение для осмотического давления коллоидных растворов будет выглядеть так:

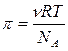или ,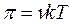

где k – константа Больцмана.

Из этого уравнения следует, что осмотическое давление увеличивается с ростом числа частиц в единице объёма даже при постоянной массе дисперсной фазы (с ростом дисперсности, например, при пептизации). Так как при одинаковой массовой концентрации n зависит от объёма частиц, то можно сказать, что осмотическое давление дисперсных (коллоидных) систем обратно пропорционально кубу радиуса их частиц.

Таким образом, закон Вант-Гоффа справедлив и для лиозолей. Однако простой расчёт показывает, что при одинаковой массовой концентрации частичные концентрации золей и тем более грубодисперсных систем обычно очень малы по сравнению с концентрацией молекул в истинных растворах. Поэтому в соответствии с выведенным уравнением и осмотическое давление в них должно быть намного меньше, а именно, во столько раз, во сколько раз частица дисперсной фазы больше, чем отдельная молекула или ион. Так, осмотическое давление коллоидных растворов в сотни и тысячи раз меньше, чем у истинных растворов. Столь малые значения очень трудно измерить с необходимой точностью, а в грубодисперсных суспензиях, пастах и эмульсиях осмотическое давление практически отсутствует.

Следует, однако, помнить, что речь идёт только об осмотическом давлении, обусловленном частицами дисперсной фазы. Надо учитывать, что в коллоидных растворах и в других дисперсных системах обычно присутствуют растворённые низкомолекулярные вещества – или в виде примесей, или в качестве стабилизаторов. Они тоже вносят свой вклад в общее осмотическое давление, поэтому его реальное значение несколько выше, чем рассчитанное исходя только из концентрации частиц дисперсной фазы.

Ещё одной особенностью осмотического давления золей является его непостоянство. Из-за идущих в той или иной степени процессов скрытой коагуляции частичная концентрация всё время уменьшается, что и вызывает снижение p во времени.

Низкое осмотическое давление является одной из причин лечебного, в частности, обеззараживающего или вяжущего действия коллоидных лекарственных средств – колларгола, протаргола и т. п. При соприкосновении их с клетками, в том числе с микробными, начинается интенсивный осмотический приток воды внутрь клеток, что приводит к гибели микробов вследствие лизиса.

ОПТИЧЕСКИЕ СВОЙСТВА И МЕТОДЫ ИССЛЕДОВАНИЯ ДИСПЕРСНЫХ СИСТЕМ

К отличительным особенностям дисперсных систем относятся их характерные оптические свойства. Изучение особенностей прохождения света через различные системы позволяет определять в них наличие и концентрацию частиц дисперсной фазы. На явлениях, сопровождающих прохождение света через дисперсные системы, основаны принципы широко применяемых методов анализа - микроскопии (оптической, электронной, ультрафиолетовой, ультрамикроскопии), нефелометрии, турбидиметрии.

Дата добавления: 2013-12-12