Расчетно-графическая работа № 1

Задача № 2

Задача № 1

Контрольные задания

Вопросы для самоанализа

Выводы

Рассмотрим алгоритм построения точки А (табл. 2.5)

Примеры решения задач в I октанте

Пример построения третьей проекции точки по двум заданным

Второе

Первое

1. две проекции точки принадлежат одной линии связи;

2. две проекции точки определяют положение третьей ее проекции;

3. линии связи перпендикулярны соответствующей оси проекций.

Любая точка пространства задается координатами. По знакам координат можно определить октант, в котором находится заданная точка. Для этого воспользуемся табл. 2.3, в которой рассмотрены знаки координат в 1–4 октантах (5–8 октанты не представлены, они имеют отрицательное значение х, а y и z повторяются).

Таблица 2.3

x	y	z	Октант
+	+	+	I
+	_	+	II
+	_	_	III
+	+	_	IV

Образование комплексного чертежа в системе трех плоскостей проекций осуществляется совмещением плоскостей p₁, p₂, p₃ (рис. 2.31).

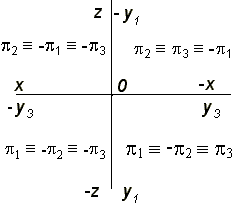
Рис. 2.31

Ось у в этом случае имеет два положения: y₁ c плоскостью p₁, y₃ c плоскостью p₃.

Горизонтальная и фронтальная проекции точки располагаются на линии проекционной связи, перпендикулярной оси x, фронтальная и профильная проекции – на линии проекционной связи, перпендикулярной к оси z.

А₁А_Х = А₃А_Z = АА₂ – расстояние от А до p₂

А₂А_Х = А₃А_y = АА₁ – расстояние отА до p₁

А₁А_y = А₂А_Z = АА₃ – расстояние от А до p₃

Расстояние точки от плоскости проекций измеряются аналогично отрезкам на эпюре (рис. 2.32).

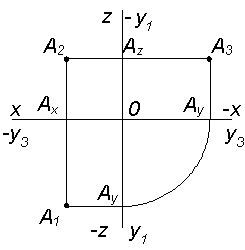
Рис. 2.32

При построении проекции точки в пространстве и на комплексном чертеже могут применяться различные алгоритмы.

1. Алгоритм построения наглядного изображения точки, заданной координатами (рис. 2.30):

1.1. Соотнести знаки координат x, y, z с данными табл. 2.3.

1.2. Определить четверть, в которой расположена точка.

1.3. Выполнить наглядное (аксонометрическое) изображение четверти.

1.4. Отложить координаты точки на осях А_Х, А_Y, А_Z.

1.5. Построить проекции точки на плоскостях p₁, p₂, p_3.

1.6. Построить перпендикуляры к плоскостям p₁, p₂, p₃ в точках проекции А₁, А₂, А₃.

1.7. Точка пересечения перпендикуляров есть искомая точка А.

2. Алгоритм построения комплексного чертежа точки в системе трех плоскостей проекций p ₁, p ₂, p ₃, заданной координатами (рис. 2.32)

2.1. Определить по координатам четверть, в которой расположена точка.

2.2. Определить механизм совмещения плоскостей.

2.3. Построить комплексный чертеж четверти.

2.4. Отложить координаты точки на осях x, y, z (А_Х, А_Y, А_Z).

2.5. Построить проекции точки на комплексном чертеже.

§ 7. Комплексный чертеж и наглядное изображение точки в I–IV октантах

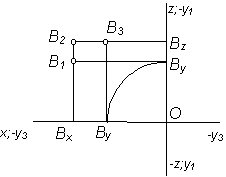
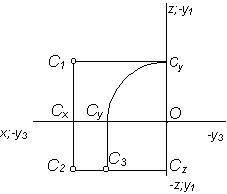
Рассмотрим пример построения точек А, В, С, D в различных октантах (табл. 2.4).

Таблица 2.4

Октант	Наглядное изображение	Комплексный чертеж
I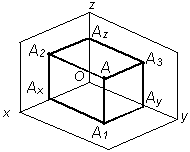
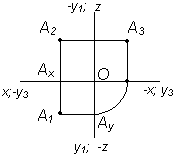
II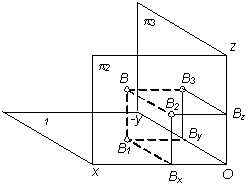
III
IV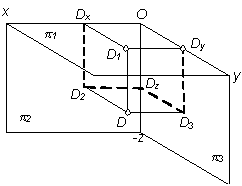

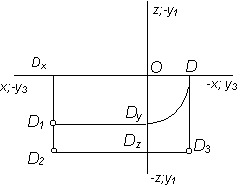
Точка в пространстве определяется любыми двумя своими проекциями. При необходимости построения третьей проекции по двум заданным необходимо воспользоваться соответствием отрезков линий проекционной связи, полученных при определении расстояний от точки до плоскости проекций (см. рис. 2.27 и рис. 2.28).

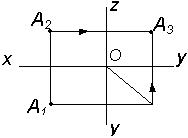
Дано А1; А2	Построить А3
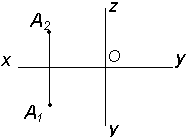
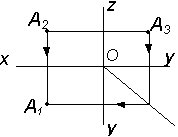
Дано А2; А3	Построить А1
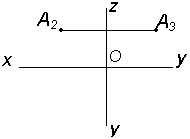
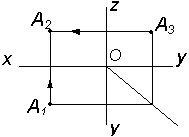
Дано А1; А3	Построить А2

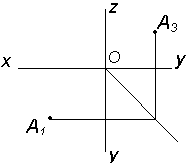
Таблица 2.5

Алгоритм построения точки А
по заданным координатам А (x = 5, y = 20, z = -9)

Вербальная форма	Графическая форма
Соотнести знаки координат x, y, z с данными табл. 2.3	Согласно табл. 2.3, это знаки 4-го октанта
Построить наглядное (аксонометрическое) изображение 4-го октанта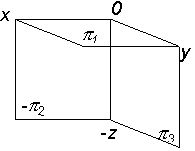
Определить механизм совмещения плоскостей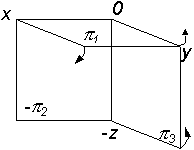
Построить комплексный чертеж 4-го октанта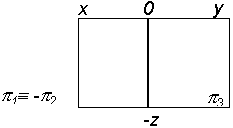
Отложить координаты точки на осях: x = 5, y = 20, z = -9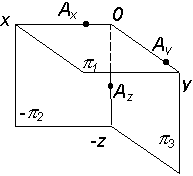

Перенести координаты точки на оси комплексного чертежа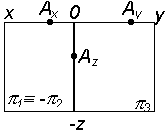
Построить горизонтальную, фронтальную и профильную проекции точки А (табл. 2.4)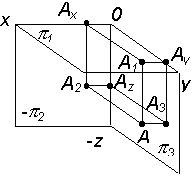
Построить проекции точки А (А1, А2, А3) на комплексном чертеже (табл. 2.4)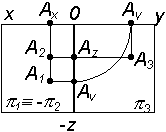

В следующих главах мы будем рассматривать образы: прямые и плоскости только в первой четверти. Хотя все рассматриваемые способы можно применить в любой четверти.

Таким образом, на основании теории Г. Монжа, можно преобразовать пространственное изображение образа (точки) в плоскостное.

Эта теория основывается на следующих положениях:

1. Все пространство делится на 4 четверти с помощью двух взаимно перпендикулярных плоскостей p₁ и p₂, либо на 8 октантов при добавлении третьей взаимно-перпендикулярной плоскости p₃.

2. Изображение пространственного образа на эти плоскости получается с помощью прямоугольного (ортогонального) проецирования.

3. Для преобразования пространственного изображения в плоскостное считают, что плоскость p₂ – неподвижна, а плоскость p₁ вращается вокруг оси x так, что положительная полуплоскость p₁ совмещается с отрицательной полуплоскостью p₂, отрицательная часть p₁ – с положительной частью p₂.

4. Плоскость p₃ вращается вокруг оси z (линии пересечения плоскостей) до совмещения с плоскостью p₂ (см. рис. 2.31).

Изображения, получающиеся на плоскостях p₁, p₂ и p₃ при прямоугольном проецировании образов, называются проекциями.

Плоскости p₁, p₂ и p₃ вместе с изображенными на них проекциями, образуют плоскостной комплексный чертеж или эпюр.

Линии, соединяющие проекции образа ^ осям x, y, z, называются линиями проекционной связи.

Для более точного определения образов в пространстве может быть применена система трех взаимно перпендикулярных плоскостей p₁, p ₂, p ₃.

В зависимости от условия задачи можно выбрать для изображения либо систему p₁, p₂, либо p₁, p₂, p₃.

Систему плоскостей p₁, p₂, p₃ можно соединить с системой декартовых координат, что дает возможность задавать объекты не только графическим или (вербальным) образом, но и аналитическим (с помощью цифр).

Такой способ изображения образов, в частности точки, дает возможность решать такие позиционные задачи, как:

• расположение точки относительно плоскостей проекций (общее положение, принадлежность плоскости, оси);
• положение точки в четвертях (в какой четверти расположена точка);
• положение точек относительно друг друга, (выше, ниже, ближе, дальше относительно плоскостей проекций и зрителя);
• положение проекций точки относительно плоскостей проекций (равноудаление, ближе, дальше).

Метрические задачи:

• равноудаленность проекции от плоскостей проекций;
• отношение удаления проекции от плоскостей проекций (в 2–3 раза, больше, меньше);
• определение расстояния точки от плоскостей проекций (при введении системы координат).

1. Линией пересечения каких плоскостей является ось z?

2. Линией пересечения каких плоскостей является ось y?

3. Как располагается линия проекционной связи фронтальной и профильной проекции точки? Покажите.

4. Какими координатами определяется положение проекции точки: горизонтальной, фронтальной, профильной?

5. В какой четверти располагается точка F (10; –40; –20)? От какой плоскости проекций точка F удалена дальше всего?

6. Расстоянием от какой проекции до какой оси определяется удаление точки от плоскости p₁? Какой координатой точки является это расстояние?

Основные понятия, которые необходимо знать:

– система двух и трех плоскостей проекций;

– фронтальная проекция, горизонтальная проекция, профильная проекция, комплексный чертеж (эпюр);

– линии проекционной связи.

Способы деятельности, которыми надо уметь пользоваться:

• алгоритм построения точки, заданной координатами в системе трех плоскостей проекций в пространстве и на комплексном чертеже;
• построение третьей проекции по двум заданным.

1. Дать сравнительный анализ положения проекций точек в четвертях (см. табл. 2.5): по сходству, различию, противоположности (рис. 2.33 и рис. 2.34).

Определить координаты точек и их взаимное положение в пространстве (рис. 2.33 и рис. 2.34)

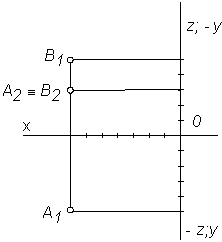
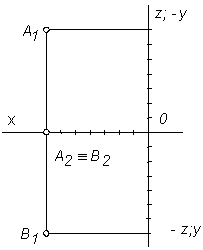
Рис. 2.33	Рис. 2.34

Построить проекции точки:

1. расположенной во II четверти и равноудаленной от всех трех плоскостей проекций;

2. расположенной в IV четверти, расстояние которой от плоскости p₁=0.

Построение наглядного изображения и комплексного чертежа точки
в системе трех плоскостей проекций

Задания (выполняются в соответствии с вариантом, указанным в нижеследующей таблице)

1. По заданным координатам построить три проекции точек А, В, С.

2. Определить, в каком октанте находятся точки.

1. Выполнить наглядные изображения и комплексный чертеж данных точек.

Дата добавления: 2013-12-12