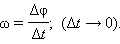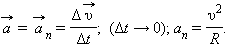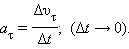КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Движение по окружности
|
|
|
|
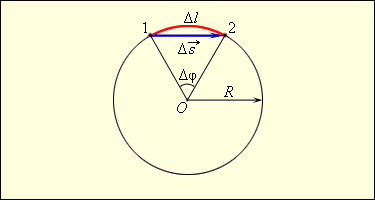
Движение тела по окружности является частным случаем криволинейного движения. Наряду с вектором перемещения 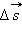 удобно рассматривать угловое перемещение Δφ (или угол поворота), измеряемое в радианах (рис. 1.6.1). Длина дуги связана с углом поворота соотношением
удобно рассматривать угловое перемещение Δφ (или угол поворота), измеряемое в радианах (рис. 1.6.1). Длина дуги связана с углом поворота соотношением
| Δ l = R Δφ. |
При малых углах поворота Δ l ≈ Δ s.
|
Рисунок 1.6.1.
Линейное 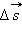 и угловое и угловое 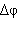 перемещения при движении тела по окружности перемещения при движении тела по окружности
|
Угловой скоростью ω тела в данной точке круговой траектории называют предел (при Δ t → 0) отношения малого углового перемещения Δφ к малому промежутку времени Δ t:
|
Угловая скорость измеряется в рад/с.
Связь между модулем линейной скорости υ и угловой скоростью ω:
| υ = ω R. |
При равномерном движении тела по окружности величины υ и ω остаются неизменными. В этом случае при движении изменяется только направление вектора 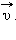
Равномерное движение тела по окружности является движением с ускорением. Ускорение
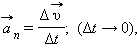
|
направлено по радиусу к центру окружности. Его называют нормальным или центростремительным ускорением. Модуль центростремительного ускорения связан с линейной υ и угловой ω скоростями соотношениями:
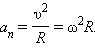
|
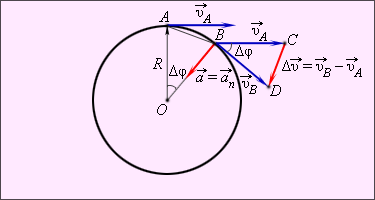
Для доказательства этого выражения рассмотрим изменение вектора скорости 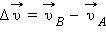 за малый промежуток времени Δ t. По определению ускорения
за малый промежуток времени Δ t. По определению ускорения
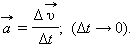
|
Векторы скоростей 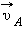 и
и 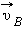 в точках A и B направлены по касательным к окружности в этих точках. Модули скоростей одинаковы υ A = υ B = υ.
в точках A и B направлены по касательным к окружности в этих точках. Модули скоростей одинаковы υ A = υ B = υ.
Из подобия треугольников OAB и BCD (рис. 1.6.2) следует:
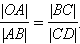
|
|
Рисунок 1.6.2.
Центростремительное ускорение тела 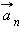 при равномерном движении по окружности при равномерном движении по окружности
|
При малых значениях угла Δφ = ωΔ t расстояние | AB | =Δ s ≈ υΔ t. Так как | OA | = R и | CD | = Δυ, из подобия треугольников на рис. 1.6.2 получаем:
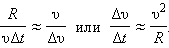
|
При малых углах Δφ направление вектора 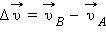 приближается к направлению на центр окружности. Следовательно, переходя к пределу при Δ t → 0, получим:
приближается к направлению на центр окружности. Следовательно, переходя к пределу при Δ t → 0, получим:
|
При изменении положения тела на окружности изменяется направление на центр окружности. При равномерном движении тела по окружности модуль ускорения остается неизменным, но направление вектора ускорения изменяется со временем. Вектор ускорения в любой точке окружности направлен к ее центру. Поэтому ускорение при равномерном движении тела по окружности называется центростремительным.
В векторной форме центростремительное ускорение может быть записано в виде
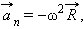
|
где 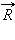 – радиус-вектор точки на окружности, начало которого находится в ее центре.
– радиус-вектор точки на окружности, начало которого находится в ее центре.
Если тело движется по окружности неравномерно, то появляется также касательная (или тангенциальная) составляющая ускорения (см. §1.1):
|
В этой формуле Δυτ = υ2 – υ1 – изменение модуля скорости за промежуток времени Δ t.
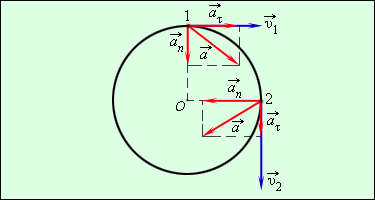
Направление вектора полного ускорения  определяется в каждой точке круговой траектории величинами нормального и касательного ускорений (рис. 1.6.3).
определяется в каждой точке круговой траектории величинами нормального и касательного ускорений (рис. 1.6.3).
|
Рисунок 1.6.3.
Составляющие ускорения 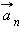 и и 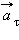 при неравномерном движении тела по окружности при неравномерном движении тела по окружности
|
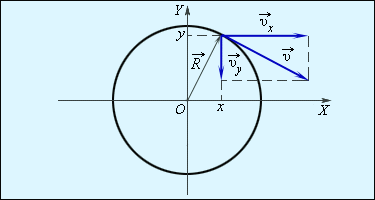
Движение тела по окружности можно описывать с помощью двух координат x и y (плоское движение). Скорость тела в каждый момент можно разложить на две составляющие υ x и υ y (рис. 1.6.4).
При равномерном вращении тела величины x, y, υ x, υ y будут периодически изменяться во времени по гармоническому закону с периодом
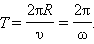
|
|
Рисунок 1.6.4.
Разложение вектора скорости  по координатным осям по координатным осям
|
|
|
|
|
|
Дата добавления: 2013-12-12; Просмотров: 537; Нарушение авторских прав?; Мы поможем в написании вашей работы!