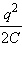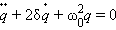RLC-контур. Свободные колебания

Общность колебательных и волновых закономерностей проявляется в общности математических уравнений, описывающих процессы различной физической природы.

Глава 2. Электромагнитные колебания и волны

Колебательные и волновые процессы, изучаемые в различных разделах физики, проявляют удивительную общность закономерностей. Колебания груза на пружине и процессы в электрическом колебательном контуре, колебания столба воздуха в органной трубе и ход механических часов, распространение света и звуковых волн и т. д. – все эти явления протекают очень похожим образом. Однако, они имеют различную физическую природу. Чтобы решить, например, задачу о колебаниях груза на пружине, нужно знать законы Ньютона, решение задачи о колебаниях в электрическом контуре требует знания законов электродинамики. Но математические уравнения, описывающие процессы, происходящие в этих двух системах, оказываются одинаковыми. Аналогично обстоит дело и с волновыми процессами.

Поэтому при изучении электромагнитных колебаний и волн мы будем обращаться за аналогиями к главе «Механические колебания и волны» (часть I, гл. II).

В электрических цепях, так же как и в механических системах, таких как груз на пружине или маятник, могут возникать свободные колебания. Простейшей электрической системой, способной совершать свободные колебания, является последовательный RLC -контур (рис. 2.2.1).

Рисунок 2.2.1. Последовательный RLC -контур

Когда ключ K находится в положении 1, конденсатор заряжается до напряжения 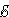. После переключения ключа в положение 2 начинается процесс разрядки конденсатора через резистор R и катушку индуктивности L. При определенных условиях этот процесс может иметь колебательный характер.

Закон Ома для замкнутой RLC -цепи, не содержащей внешнего источника тока, записывается в виде

где – напряжение на конденсаторе, q – заряд конденсатора, – ток в цепи. В правой части этого соотношения стоит ЭДС самоиндукции катушки. Если в качестве переменной величины выбрать заряд конденсатора q (t), уравнение, описывающее свободные колебания в RLC -контуре, может быть приведено к следующему виду:

Рассмотрим сначала случай, когда в контуре нет потерь электромагнитной энергии (R = 0). Тогда

(*)

Здесь принято обозначение: Уравнение (*) описывает свободные колебания в LC -контуре в отсутствие затухания. По виду оно в точности совпадает с уравнением свободных колебаний груза на пружине в отсутствие сил трения (ч. I, § 2.2). Рис. 2.2.2 иллюстрирует аналогию процессов свободных электрических и механических колебаний. На рисунке приведены графики изменения заряда q (t) конденсатора и смещения x (t) груза от положения равновесия, а также графики тока J (t) и скорости груза υ (t) за один период 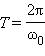колебаний.

Рисунок 2.2.2. Аналогия процессов свободных электрических и механических колебаний

Сравнение свободных колебаний груза на пружине и процессов в электрическом колебательном контуре позволяет сделать заключение об аналогии между электрическими и механическими величинами. Эти аналогии представлены в таблице 1.

Электрические величины	Механические величины
Заряд конденсатора	q (t)	Координата	x (t)
Ток в цепи		Скорость
Индуктивность	L	Масса	m
Величина, обратная электроемкости		Жесткость	k
Напряжение на конденсаторе		Упругая сила	kx
Энергия электрического поля конденсатора		Потенциальная энергия пружины
Магнитная энергия катушки		Кинетическая энергия
Магнитный поток	LI	Импульс	m υ

Таблица 1

В отсутствие затухания свободные колебания в электрическом контуре являются гармоническими, то есть происходят по закону

q (t) = q ₀ cos(ω t + φ₀).

Параметры L и C колебательного контура определяют только собственную частоту свободных колебаний

Амплитуда q ₀ и начальная фаза φ₀ определяются начальными условиями, то есть тем способом, с помощью которого система была выведена из состояния равновесия. В частности, для процесса колебаний, который начнется в контуре (рис. 2.2.1) после переключения ключа K в положение 2, q ₀ = C 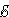, φ₀ = 0.

При свободных колебаниях происходит периодическое превращение электрической энергии W _э, запасенной в конденсаторе, в магнитную энергию W _м катушки и наоборот. Если в колебательном контуре нет потерь энергии, то полная электромагнитная энергия системы остается неизменной:

Все реальные контуры содержат электрическое сопротивление R. Процесс свободных колебаний в таком контуре уже не подчиняется гармоническому закону. За каждый период колебаний часть электромагнитной энергии, запасенной в контуре, превращается в джоулево тепло, и колебания становятся затухающими (рис. 2.2.3).

Рисунок 2.2.3. Затухающие колебания в контуре

Затухающие колебания в электрическом контуре аналогичны затухающим колебаниям груза на пружине при наличии вязкого трения, когда сила трения изменяется прямо пропорционально скорости тела: F _тр = – βυ. Коэффициент β в этой формуле аналогичен сопротивлению R электрического контура. Уравнение свободных колебаний в контуре при наличии затухания имеет вид

(**)

Физическая величина δ = R / 2 L называется коэффициентом затухания. Решением этого дифференциального уравнения является функция

которая содержит множитель exp (–δ t), описывающий затухание колебаний. Скорость затухания зависит от электрического сопротивления R контура. Интервал времени в течение которого амплитуда колебаний уменьшается в e ≈ 2,7 раза, называется временем затухания.

В § 2.4 части 1 было введено понятие добротности Q колебательной системы:

где N – число полных колебаний, совершаемых системой за время затухания τ. Добротности Q любой колебательной системы, способной совершать свободные колебания, может быть дано энергетическое определение:

Для RLC -контура добротность Q выражается формулой

Добротность электрических контуров, применяемых в радиотехнике, обычно порядка нескольких десятков и даже сотен.

Следует отметить, что собственная частота ω свободных колебаний в контуре с не очень высокой добротностью несколько меньше собственной частоты ω₀ идеального контура с теми же значениями L и C. Но при Q ≥ (5÷10) этим различием можно пренебречь.

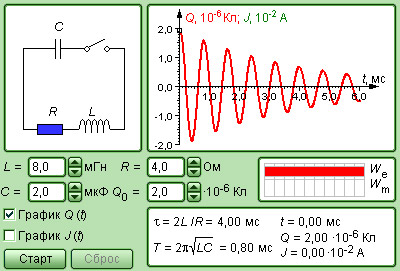
Модель. Свободные колебания в RLC-контуре

Дата добавления: 2013-12-12