Теория устойчивости Ляпунова.

Кроме перечисленных вопросов необходимо владеть минимумом остаточных знаний из

первой части курса в виде определений и понятий: автоматическая система (АС); объект управления; регулятор, обратная связь; принцип управления по отклонению; астатическая и статическая АС; передаточная функция; переходная функция; комплексная передаточная функция; АЧХ; ФЧХ; логарифмические частотные характеристики; формулы типовых соединений звеньев; передаточные функции замкнутых АС; построение ЛАХ разомкнутых АС.

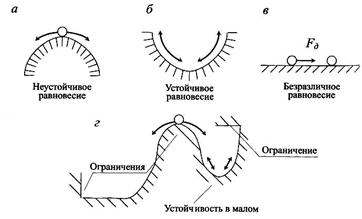
1. Устойчивость в широком смысле. Примеры устойчивости и неустойчивости. Определение устойчивости по Л.М. Ляпунову. Асимптотическая устойчивость.

Устойчивость системы- способность системы сохранять свои свойства достаточно длительный промежуток времени, при действии на нее возмущающих факторов.

Это критерий физической реализуемости свойств системы а следовательно и самой системы.

Неустойчивость системы также важна

Только при неустойчивости можно получить устойчивую систему.

Важнейшим свойством действительности является движение в том числе относительный покой.

Движение АС- изменение ее выходной координаты y(t)

Невозмущенное движение- движение, для реализации которого создано АС при заданном выходном сигнале.

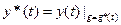-невозмущенное(1)

Всегда существуют малые причины отклонения в силу которых могут возникать большие следствия.

При устойчивости малые причины не должны вызывать больших отклонений от невозмущенного движения.

Возмущение- отклонение Н.У. от нулевых.

Любое движение, отличное от невозмущенного назовем возмущенным

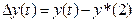-отклонение возмущенного движения от невозмущенного.

ð y(0)-начальное отклонение возмущенного движения от невозмущенного

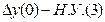
Определение Если для сколь угодно малого положительного произвольного числа 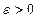найдется такое положительное число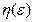такое что из условия 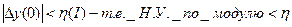следует что при t>0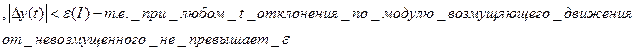то невозмущенное движение будем считать устойчивым.

Если с течением времени возмущенное движение сколь угодно близко приближено к невозмущенному, то невозмущенное движение называется асимптотически устойчивым

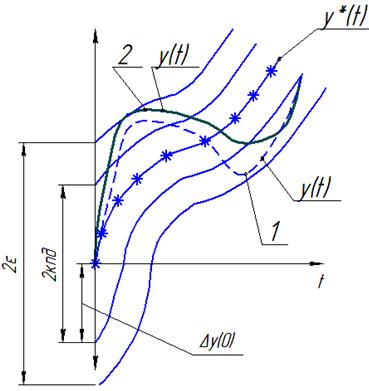
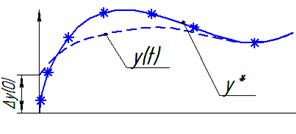
2Е -полоса возмущающего дв-я

Невозмущающ. устойчивое движение y(t)- если для любых НУ в полосе 2кпд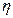

Возмущ. Дв-е не выходит из полосы 2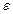

2-я неустойчивая кривая,т.к касается границы.

1. Устойчивость линеаризованных АС. Условие асимптотической устойчивости линеаризованных АС. Теоремы Ляпунова об устойчивости линеаризованных АС.

Пусть имеется АС вида:

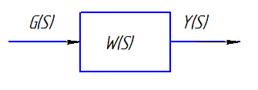
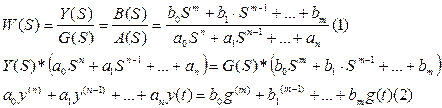
Подадим на вход АС. Сигнал 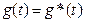для получения на выходе желаемого сигнала и применим это движение за невозмущенное

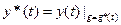(3)

Получит 3 можно доставить g(t) в правую часть уравнения (2)

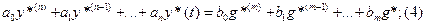
Пусть начальные условия невозмущены (не нулевые)

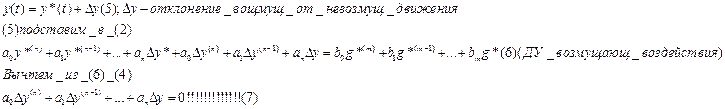
Дата добавления: 2013-12-12