Метод Борда

Правило большинства голосов

Изменим несколько результаты голосования, чтобы избежать парадокса Кондорсе. Предположим, что голоса распределились так, как показано в табл. 17. Нетрудно подсчитать, что при этих новых результатах голосования, в соответствии с принципом Кондорсе, избранным будет кандидат С, который

при попарном сравнении побеждает двух других кандидатов.

Таблица 17

Распределение голосов (правило большинства)

Число голосующих	предпочтение
	А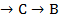

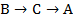
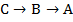
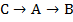
Однако если мы используем другой принцип выбора: большинство голосующих, которые назвали данного кандидата лучшим, то победителем оказывается кандидат А. Но при этом кандидат А не набрал абсолютного большинства голосов. Мы видим, что способ определения победителя при демократической

системе голосования (один человек - один голос) зависит от процедуры голосования.

Отметим еще одну процедуру голосования из множества предложенных: метод Борда [2]. Согласно этому методу, результаты голосования выражаются в виде числа баллов, набранных каждым из кандидатов. Пусть число кандидатов равно n. Тогда за первое место присуждается п баллов, за второе — п-1, за последнее

- один балл. Применим метод Борда к приведенному выше примеру (см.табл. 17). Подсчитаем число баллов для каждого из кандидатов:

А: 23-3+119-1 + 16-1 + 2-2=108;

В: 23-1 + 19-3 + 16-2 + 2-1 = 114;

С: 23-2 + 19-2 + 16-2 + 2-3=138.

В соответствии с методом Борда мы должны объявить победителем кандидата С.

Однако с методом Борда, как и с принципом Кондорсе, возникают проблемы. Предположим, что результаты голосования в выборном органе представлены табл 18. Подсчитав баллы в соответствии с методом Борда, получим: А — 124, В — 103, С —137. В соответствии с методом Борда победителем следует объявить

кандидата С. Однако в данном случае явным победителем, является кандидат А, набравший абсолютное большинство голосов: 31 из 60.

Таблица 18

Распределение голосов (метод Борда)

Число голосующих	предпочтение
	А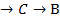

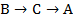
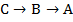
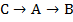
Приведенные примеры позволяют понять, что парадоксы при голосовании не возникают лишь в случае, когда победитель определяется по принципу абсолютного большинства голосов. Однако такой случай нетипичен для большинства выборов в демократических странах. Обычно число кандидатов больше, чем два, и редки случаи, когда кто-то из них сразу же получает поддержку абсолютного большинства избирателей. Интересно, что парадоксы голосования сохраняются и при введении двух туров и условии, что во второй тур выходят дча

кандидата, набравшие большинство голосов. Обратимся к табл. 16, составленной Кондорсе. В соответствии с предпочтениями во второй, тур выходят А (23 голоса) и В (19 голосов), после чего побеждает А. Однако при небольшом усилении первоначальной позиции А: предпочтения двух избирателей (3-я строка) выглядят как А -> В -> С, во второй тур выходят А (25 голосов) и С (20 голосов), после чего побеждает С. Ясно, что такой результат голосования противоречит здравому смыслу.

Дата добавления: 2013-12-12