
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Свойства векторного произведения
|
|
|
|
Векторное произведение векторов
ВЕКТОРНОЕ, СМЕШАННОЕ И ДВОЙНОЕ ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Def.Векторным произведением векторов  и
и 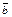 называется вектор
называется вектор 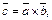 определяемый следующим образом:
определяемый следующим образом:
1) 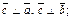
2) 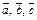 образуют правую тройку векторов;
образуют правую тройку векторов;
3) 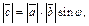 где
где 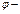 угол между
угол между  и
и 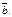
1. 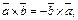 (12.1)
2. (12.1)
2. 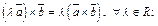 (12.2)
3. (12.2)
3. 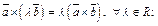 (12.3)
4. (12.3)
4. 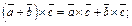 (12.4)
5. (12.4)
5. 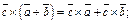 (12.5)
6. Два ненулевых вектора коллинеарны тогда и только тогда, когда их векторное произведение есть нулевой вектор.
7. Модуль векторного произведения (12.5)
6. Два ненулевых вектора коллинеарны тогда и только тогда, когда их векторное произведение есть нулевой вектор.
7. Модуль векторного произведения 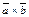 равен площади параллелограмма, построенного на векторах равен площади параллелограмма, построенного на векторах и и 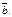
|
Доказательство.
1. Очевидно, что векторы 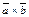 и
и 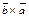 имеют одинаковые модули, коллинеарны и противоположно направлены, т.к. тройки
имеют одинаковые модули, коллинеарны и противоположно направлены, т.к. тройки 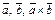 и
и 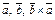 противоположной ориентации (рис. 12.1). Значит,
противоположной ориентации (рис. 12.1). Значит, 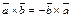
 .
.
2. Для 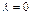 утверждение очевидно, т.к. левая и правая часть соотношения (12.2) есть нулевой вектор.
утверждение очевидно, т.к. левая и правая часть соотношения (12.2) есть нулевой вектор.
Пусть 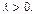 Заметим, что Заметим, что 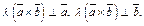 Также
Также 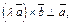 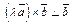 (векторы (векторы  и и 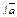 лежат в одной плоскости). Значит, векторы лежат в одной плоскости). Значит, векторы 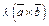 и и 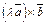 коллинеарны. Очевидно, что и направления их совпадают. Кроме того, эти векторы имеют одинаковую длину. Действительно, коллинеарны. Очевидно, что и направления их совпадают. Кроме того, эти векторы имеют одинаковую длину. Действительно, 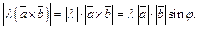
| 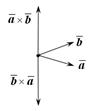 Рис. 12.1
Рис. 12.1
|
Учитывая, угол между векторами  и
и 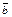 равен углу между векторами
равен углу между векторами 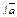 и
и 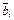 то
то 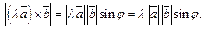 Поэтому
Поэтому 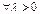
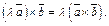 Аналогично свойство доказывается и для
Аналогично свойство доказывается и для 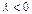
 .
.
3. Свойство 3 является непосредственным следствием свойств 1 и 2.
4. Для доказательства этого свойства воспользуемся следующей леммой.
| Lemma | Пусть имеется два вектора  и и 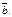 Обозначим Обозначим 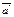 проекцию вектора проекцию вектора  на плоскость на плоскость 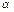 , перпендикулярную вектору , перпендикулярную вектору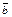 (рис. 12.2). Тогда (рис. 12.2). Тогда 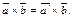
|
Доказательство леммы.
Векторы 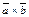 и и 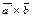 имеют равные модули. Действительно, имеют равные модули. Действительно,
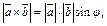 где где 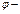 угол между угол между  и и 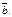
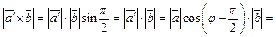
| 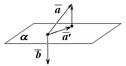 Рис. 12.2
Рис. 12.2
|
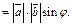
Выясним направленность этих векторов. Вектор 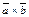 лежит в плоскости
лежит в плоскости 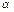 , т.к
, т.к 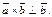 Учитывая, что
Учитывая, что 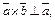 можем сделать вывод, что
можем сделать вывод, что 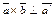 (теорема о трех перпендикулярах). Значит,
(теорема о трех перпендикулярах). Значит, 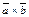 и
и 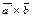 коллинеарны. Кроме того, тройки
коллинеарны. Кроме того, тройки 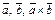 и
и 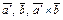 имеют одинаковую ориентацию. Значит,
имеют одинаковую ориентацию. Значит, 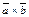 и
и 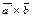 сонаправлены. Откуда заключаем, что
сонаправлены. Откуда заключаем, что 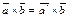
 .
.
Теперь докажем свойство 4. Соотношение (12.4) справедливо при 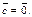 Пусть
Пусть 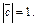 Обозначим через
Обозначим через 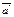 и
и 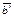 проекции векторов
проекции векторов  и
и 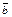 на плоскость, перпендикулярную вектору
на плоскость, перпендикулярную вектору 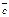 (рис. 12.3). Построим
(рис. 12.3). Построим 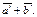 Тогда векторы
Тогда векторы 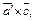
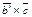 и
и 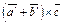 получаются из векторов
получаются из векторов 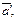
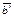 и
и 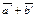 соответственно поворотом на угол
соответственно поворотом на угол 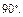 И, следовательно,
И, следовательно,
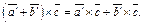
А так как, согласно доказанной лемме,
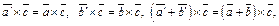
то 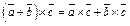
 .
.
5. Свойство 5 является непосредственным следствием свойств 1 и 4.
6. Свойство 6 непосредственно вытекает из определения векторного произведения.
7. Действительно, 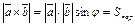 (рис. 12.3). (рис. 12.3).
| 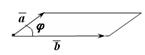 Рис. 12.3 Рис. 12.3
|
| Th.12.1 | (выражение векторного произведения через координаты сомножителей)
Если 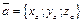 и и 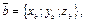 то то
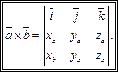 (12.6) (12.6)
|
Доказательство.
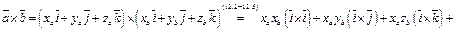
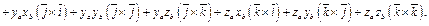
Согласно свойству 6 векторного произведения 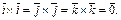 По определению
По определению 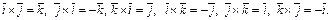
Имеем
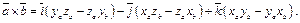
С другой стороны
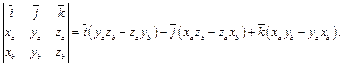
Теорема доказана  .
.
N. Найти площадь параллелограмма, построенного на векторах  и
и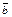 если
если 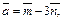
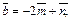 где
где 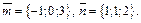
Решение.
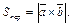 Упростим выражение
Упростим выражение 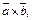 основываясь на свойствах векторного произведения.
основываясь на свойствах векторного произведения.
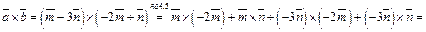
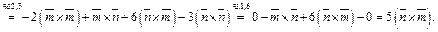
Вычислим 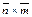 , по формуле 12.6.
, по формуле 12.6.
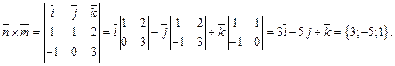
Значит, 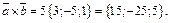
Тогда
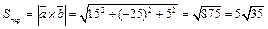 (кв. ед.)
(кв. ед.)
Ответ. 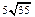 кв. ед.
кв. ед.
|
|
|
|
|
Дата добавления: 2013-12-12; Просмотров: 301; Нарушение авторских прав?; Мы поможем в написании вашей работы!