
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Плотность распределения вероятностей непрерывной
|
|
|
|
Глава 2.2. Непрерывные случайные величины.
Примеры распределений дискретной случайной величины.
Геометрическое распределение. Пусть проводится серия независимых испытаний до первого успеха, в каждом из которых вероятность появления события 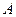 (вероятность успеха) равна
(вероятность успеха) равна 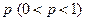 , а вероятность противоположного события
, а вероятность противоположного события 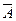 (вероятность неудачи) равна
(вероятность неудачи) равна 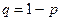 . Серия испытаний заканчивается при первом появлении события
. Серия испытаний заканчивается при первом появлении события 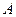 .
.
Обозначим через  дискретную случайную величину – число испытаний в рассматриваемой серии испытаний до первого успеха. Очевидно, что
дискретную случайную величину – число испытаний в рассматриваемой серии испытаний до первого успеха. Очевидно, что 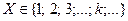 . Закон распределения данной дискретной случайной величины выражается формулой:
. Закон распределения данной дискретной случайной величины выражается формулой:
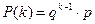 , где
, где 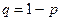 .
.
Данная случайная величина  является примером дискретной случайной величины, принимающей счётное число значений.
является примером дискретной случайной величины, принимающей счётное число значений.
Если положить в последней формуле 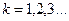 , то получим бесконечно убывающую геометрическую прогрессию:
, то получим бесконечно убывающую геометрическую прогрессию:
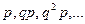 . Поэтому, такое распределение называется геометрическим распределением.
. Поэтому, такое распределение называется геометрическим распределением.
Геометрическое распределение имеет следующие числовые характеристики: 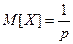 и
и 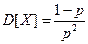 .
.
Биномиальное распределение. Рассмотрим схему Бернулли для серии из 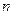 испытаний с вероятностью успеха
испытаний с вероятностью успеха 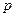 (с вероятностью неудачи
(с вероятностью неудачи 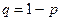 ).
).
Рассмотрим в качестве дискретной случайной величины  число появлений события
число появлений события 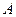 (число успехов) в
(число успехов) в 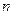 независимых испытаниях. В этом случае
независимых испытаниях. В этом случае  , причём закон распределения этой случайной величины определяется формулой Бернулли:
, причём закон распределения этой случайной величины определяется формулой Бернулли:
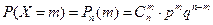 .
.
Такое распределение называется биномиальным распределением.
Пример 2.1.5.. Игральная кость бросается 2 раза. Написать закон распределения случайной величины  - числа выпадений чётной грани.
- числа выпадений чётной грани.
Решение. Случайная величина 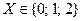 . Учитывая, что вероятность успеха в одном испытании
. Учитывая, что вероятность успеха в одном испытании 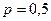 , получим:
, получим:
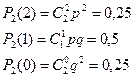
Поэтому закон распределения случайной величины  имеет вид:
имеет вид:
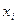
| |||
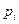
| 0,25 | 0,5 | 0,25 |
Контроль: 0,25 + 0,5 + 0,25 = 1.
Рассмотрим числовые характеристики случайной величины, распределённой по биномиальному закону.
Сопоставим каждому 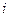 -ому испытанию случайную величину
-ому испытанию случайную величину 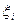 , которую назовём индикатором появления успеха в
, которую назовём индикатором появления успеха в 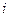 -ом испытании. Будем считать, что случайная величина
-ом испытании. Будем считать, что случайная величина 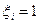 , если в
, если в 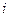 -ом испытании успех, и
-ом испытании успех, и 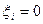 , если в
, если в 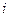 -ом испытании неудача. Для рассматриваемой схемы закон распределения случайной величины
-ом испытании неудача. Для рассматриваемой схемы закон распределения случайной величины 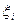 имеет вид:
имеет вид:
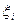
| ||
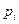
| 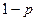
| 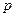
|
а числовые характеристики случайной величины 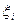 равны
равны
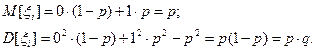
Используя величины 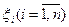 , случайную величину
, случайную величину  (число успехов в
(число успехов в 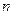 испытаниях) можно представить как
испытаниях) можно представить как 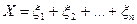 .
.
В силу независимости испытаний в схеме Бернулли, а следовательно, независимости случайных величин 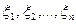 , получим:
, получим:
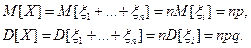
Таким образом, биномиальное распределение имеет следующие числовые характеристики:
 .
.
Распределение Пуассона. Пусть проводится 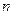 независимых испытаний по схеме Бернулли с вероятностью успеха
независимых испытаний по схеме Бернулли с вероятностью успеха 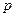 в одном испытании. В случае если число испытаний в серии
в одном испытании. В случае если число испытаний в серии 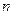 велико (
велико (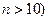 , использование формулы Бернулли сталкивается со значительными вычислительными сложностями. Тогда при больших
, использование формулы Бернулли сталкивается со значительными вычислительными сложностями. Тогда при больших 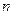 и малой вероятности успеха
и малой вероятности успеха 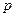 прибегают к асимптотической (т.е. приближенной, точность которой растет с увеличением
прибегают к асимптотической (т.е. приближенной, точность которой растет с увеличением 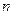 ) формуле Пуассона:
) формуле Пуассона:
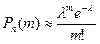 , где
, где 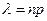 .
.
Пример 2.1.6. Пусть вероятность ошибки при приёме одного сигнала равна 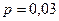 . Найти вероятность того, что при независимом приёме
. Найти вероятность того, что при независимом приёме 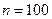 сигналов с ошибкой будет принято:
сигналов с ошибкой будет принято:
а) ровно 2 сигнала;
б) хотя бы 2 сигнала.
Решение. а) 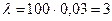 , тогда
, тогда 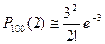
б) Ошибочный приём хотя бы двух сигналов из 100 – это приём с ошибкой двух или более сигналов. Переходя к противоположному событию (ошибочный приём 0 или 1 сигналов), получим
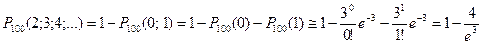 .
.
Формула Пуассона приводит к закону Пуассона, который используется не только как асимптотическое приближение формулы Бернулли, но и имеет самостоятельное значение, например, используется для описания потоков редких событий.
Дискретная случайная величина, принимающая значения 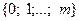 с вероятностями
с вероятностями
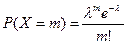 ,
,
называется распределённой по закону Пуассона с параметром 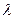 .
.
Случайная величина, распределённая по Закону Пуассона, имеет следующие числовые характеристики.

|
|
|
|
|
Дата добавления: 2013-12-11; Просмотров: 541; Нарушение авторских прав?; Мы поможем в написании вашей работы!