КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Линии магнитной индукции
|
|
|
|
Для наглядного изображения магнитного поля пользуются линиями магнитной индукции. Линией магнитной индукции называют такую линию, в каждой точке которой индукция магнитного поля (вектор 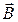 ) направлена по касательной к кривой. Направление этих линий совпадает с направлением поля. Условились линии магнитной индукции проводить так, чтобы число этих линий, приходящихся на единицу площади площадки, перпендикулярной к ним, равнялось бы модулю индукции в данной области поля. Тогда по густоте линий магнитной индукции судят о магнитном поле. Там, где линии гуще, модуль индукции магнитного поля больше. Линии магнитной индукции всегда замкнуты в отличие от линий напряжённости электростатического поля, которые разомкнуты (начинаются и заканчиваются на зарядах). Направление линий магнитной индукции находится по правилу правого винта: если поступательное движение винта совпадает с направлением тока, то его вращение происходит в направлении линий магнитной индукции. В качестве примера приведём картину линий магнитной индукции прямого тока, текущего перпендикулярно к плоскости чертежа от нас за чертёж (рис. 2).
) направлена по касательной к кривой. Направление этих линий совпадает с направлением поля. Условились линии магнитной индукции проводить так, чтобы число этих линий, приходящихся на единицу площади площадки, перпендикулярной к ним, равнялось бы модулю индукции в данной области поля. Тогда по густоте линий магнитной индукции судят о магнитном поле. Там, где линии гуще, модуль индукции магнитного поля больше. Линии магнитной индукции всегда замкнуты в отличие от линий напряжённости электростатического поля, которые разомкнуты (начинаются и заканчиваются на зарядах). Направление линий магнитной индукции находится по правилу правого винта: если поступательное движение винта совпадает с направлением тока, то его вращение происходит в направлении линий магнитной индукции. В качестве примера приведём картину линий магнитной индукции прямого тока, текущего перпендикулярно к плоскости чертежа от нас за чертёж (рис. 2).
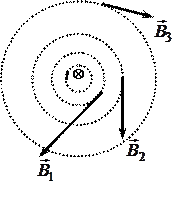 Рис. 2 Рис. 2
|
ЗАКОН ПОЛНОГО ТОКА
В электростатике было введено понятие циркуляции напряжённости электрического поля. Аналогичная величина вводится и при рассмотрении магнитного поля. Циркуляцией индукции магнитного поля называют интеграл
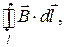 (3)
(3)
где 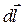 — элементарный вектор длины контура, направленный в сторону обхода контура.
— элементарный вектор длины контура, направленный в сторону обхода контура.


  Рис. 3 Рис. 3
|
Найдём циркуляцию индукции магнитного поля по окружности произвольного радиуса a, совпадающей с линией магнитной индукции. Поле создаётся током силой I, текущим по бесконечно длинному проводнику, расположенным перпендикулярно к плоскости чертежа (рис. 3). Индукция магнитного поля 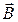 направлена по касательной к линии магнитной индукции. Преобразуем выражение
направлена по касательной к линии магнитной индукции. Преобразуем выражение 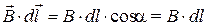 , так какa = 0иcosa = 1. Индукция магнитного поля, создаваемого током, текущим по бесконечно длинному проводнику, вычисляется по формуле: B = m0m I/ (2p a), то
, так какa = 0иcosa = 1. Индукция магнитного поля, создаваемого током, текущим по бесконечно длинному проводнику, вычисляется по формуле: B = m0m I/ (2p a), то 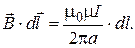 Циркуляцию вектора
Циркуляцию вектора 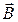 по данному контуру, находим по формуле (3):
по данному контуру, находим по формуле (3): 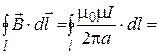
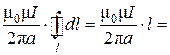
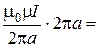 , так как
, так как 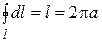 — длина окружности. Итак,
— длина окружности. Итак, 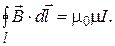 Можно показать, что это соотношение справедливо для контура произвольной формы, охватывающего проводник с током. Если магнитное поле создано системой токов I 1, I 2,..., I n, то циркуляция индукции магнитного поля по замкнутому контуру, охватывающим эти токи, равна
Можно показать, что это соотношение справедливо для контура произвольной формы, охватывающего проводник с током. Если магнитное поле создано системой токов I 1, I 2,..., I n, то циркуляция индукции магнитного поля по замкнутому контуру, охватывающим эти токи, равна
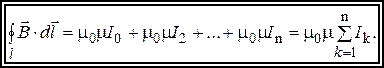 (4)
(4)
Соотношение (4) и является законом полного тока: циркуляция индукции магнитного поля по произвольному замкнутому контуру равна произведению магнитной постоянной, магнитной проницаемости на алгебраическую сумму сил токов, охватываемых этим контуром.
Силу тока можно найти, используя плотность тока j: 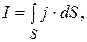 где S —площадь поперечного сечения проводника. Тогда закон полного тока записывается в виде
где S —площадь поперечного сечения проводника. Тогда закон полного тока записывается в виде
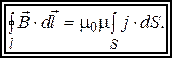 (5)
(5)
МАГНИТНЫЙ ПОТОК.
По аналогии с потоком напряжённости электрического поля вводится поток индукции магнитного поля или магнитный поток. Магнитным потоком через некоторую поверхность называют число линий магнитной индукции, пронизывающих её. Пусть в неоднородном магнитном поле находится поверхность площадью S. Для нахождения магнитного потока через неё мысленно разделим поверхность на элементарные участки площадью dS, которые можно считать плоскими, а поле в их пределах однородным (рис. 4). Тогда элементарный магнитный поток dФ Bчерез эту поверхность равен: dФ B = B·dS· cos = B n dS, где B — модуль индукции магнитного поля в месте расположения площадки, — угол между вектором 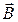 и нормалью
и нормалью 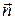 к площадке, B n = B· cos — проекция индукции магнитного поля на направление нормали. Магнитный поток Ф B через всю поверхность равен сумме этих потоков dФ B, т.е.
к площадке, B n = B· cos — проекция индукции магнитного поля на направление нормали. Магнитный поток Ф B через всю поверхность равен сумме этих потоков dФ B, т.е.


       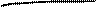     Рис. 4 Рис. 4
|
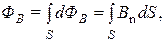 (6)
(6)
поскольку суммирование бесконечно малых величин — это интегрирование.
В системе единиц СИ магнитный поток измеряется в веберах (Вб). 1 Вб = 1 Тл·1 м2.
ТЕОРЕМА ГАУССА ДЛЯ МАГНИТНОГО ПОЛЯ
В электродинамике доказывается следующая теорема: магнитный поток, пронизывающий произвольную замкнутую поверхность, равен нулю, т.е.
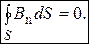 (7)
(7)
Это соотношение получило название теоремы Гаусса для магнитного поля. Эта теорема является следствием того, что в природе не существует "магнитных зарядов" (в отличие от электрических) и линии магнитной индукции всегда замкнуты (в отличие от линий напряжённости электростатического поля, которые начинаются и заканчиваются на электрических зарядах).
РАБОТА ПО ПЕРЕМЕЩЕНИЮ ПРОВОДНИКА С ТОКОМ В МАГНИТНОМ ПОЛЕ
 
|
Известно, что на проводник с током в магнитном поле действует сила Ампера. Если проводник перемещается, то при его движении эта сила совершает работу. Определим её для частного случая. Рассмотрим электрическую цепь, один из участков DC которой может скользить (без трения) по контактам. При этом цепь образует плоский контур. Этот контур находится в однородном магнитном поле с индукцией 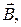 перпендикулярной к плоскости контура, направленном на нас (рис. 5). На участок DC действует сила Ампера,
перпендикулярной к плоскости контура, направленном на нас (рис. 5). На участок DC действует сила Ампера,
F = BIl· sina =BIl, (8)
где l — длина участка, I — сила тока, текущего по проводнику. — угол между направлениями тока и магнитного поля. (В данном случае= 90°иsin = 1). Направление силы находим по правилу левой руки. При перемещении участка DC на элементарное расстояние dx совершается элементарная работа dA, равная dA = F·dx. Учитывая (8), получаем:
dA = BIl·dx = IB·dS = I·dФ B, (9)
поскольку dS = l·dx — площадь, описываемая проводником при своём движении, dФ B =B·dS — магнитный поток через эту площадь или изменение магнитного потока через площадь плоского замкнутого контура. Выражение (9) справедливо и для неоднородного магнитного поля. Таким образом, работа по перемещению замкнутого контура с постоянным током в магнитном поле равна произведению силы тока на изменение магнитного потока через площадь этого контура.
ЯВЛЕНИЕ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ
Явление электромагнитной индукции заключается в следующем: при всяком изменении магнитного потока, пронизывающего площадь, охватываемую проводящим контуром, в нём возникает электродвижущая сила. Её называют э.д.с. индукции. Если контур замкнут, то под действием э.д.с. появляется электрический ток, названный индукционным.
Рассмотрим один из опытов, проведённых Фарадеем, по обнаружению индукционного тока, следовательно, и э.д.с. индукции. Если в соленоид, замкнутый на очень чувствительный электроизмерительный прибор (гальванометр) (рис. 6), вдвигать или выдвигать магнит, то при движении магнита наблюдается отклонение стрелки гальванометра, свидетельствующее о возникновении индукционного тока. То же самое наблюдается при движении соленоида относительно магнита. Если же магнит и соленоид неподвижны относительно друг друга, то и индукционный ток не возникает. Таким образом, при взаимном движении указанных тел происходит изменение магнитного потока, создаваемого магнитным полем магнита, через витки соленоида, что и приводит к появлению индукционного тока, вызванного возникающей э.д.с. индукции.
                           Рис. 6 Рис. 6
|
ПРАВИЛО ЛЕНЦА
Направление индукционного тока определяется правилом Ленца: индукционный ток всегда имеет такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, которое вызывает этот ток. Из этого следует, что при возрастании магнитного потока возникающий индукционный ток будет иметь такое направление, чтобы порождаемое им магнитное поле было направлено против внешнего поля, противодействуя увеличению магнитного потока. Уменьшение магнитного потока, наоборот, приводит к появлению индукционного тока, создающего магнитное поле, совпадающее по направлению с внешним полем.
  
                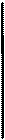   Рис. 7 Рис. 7
|
Пусть, например, в однородном магнитном поле находится квадратная рамка, изготовленная из металла и пронизываемая магнитным полем (рис.7). Предположим, что магнитное поле возрастает. Это приводит к увеличению магнитного потока через площадь рамки. Согласно правилу Ленца, магнитное поле, возникающего индукционного тока будет направлено против внешнего поля, т.е. вектор 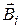 этого поля противоположен вектору
этого поля противоположен вектору 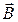 . Применяя правило правого винта (если винт вращать так, чтобы его поступательное движение совпадало с направлением магнитного поля, то его вращательное движение даёт направление тока), находим направление индукционного тока Ii.
. Применяя правило правого винта (если винт вращать так, чтобы его поступательное движение совпадало с направлением магнитного поля, то его вращательное движение даёт направление тока), находим направление индукционного тока Ii.
ЗАКОН ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ.
Закон электромагнитной индукции, определяющий возникающую э.д.с., был открыт Фарадеем опытным путём. Однако его можно получить, исходя из закона сохранения энергии.
Вернёмся к электрической цепи, приведённой на рис. 5, помещённой в магнитное поле. Найдём работу, совершаемую источником тока с э.д.с. e за элементарный промежуток времени dt, при перемещении зарядов по цепи. Из определения э.д.с. работа dA сторсторонних сил равна: dA стор = e·dq, где dq — величина заряда, протекающего по цепи за время dt. Но dq = I·dt, где I — сила тока в цепи. Тогда
dA стор= e·I·dt. (10)
Работа источника тока расходуется на выделение некоторого количества теплоты dQ и на работу dA по перемещению проводника DC в магнитном поле. Согласно закону сохранения энергии, должно выполняться равенство
dA стор= dQ + dA. (11)
Из закона Джоуля — Ленца запишем:
dQ = I 2 R·dt, (12)
где R — полное сопротивление данной цепи, а из выражения (9)
dA = I·dФ B, (13)
где dФ B— изменение магнитного потока через площадь замкнутого контура при движении проводника. Подставляя выражения (10), (12) и (13) в формулу (12), после сокращения на I, получаем e · dt = IR·dt + dФ B. Разделив обе части этого равенства на dt, находим: I = (e –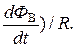 Из этого выражения следует вывод, что в цепи, кроме э.д.с. e, действует ещё какая-то электродвижущая сила ei, равная
Из этого выражения следует вывод, что в цепи, кроме э.д.с. e, действует ещё какая-то электродвижущая сила ei, равная
 (14)
(14)
и обусловленная изменением магнитного потока, пронизывающего площадь контура. Эта э.д.с. и является э.д.с. электромагнитной индукции или коротко э.д.с. индукции. Соотношение (14) представляет собой закон электромагнитной индукции, который формулируется: э.д.с. индукции в контуре равна скорости изменения магнитного потока, пронизывающего площадь, охватываемую этим контуром. Знак минус в формуле (14) является математическим выражением правила Ленца.
ЛЕКЦИЯ №10
|
|
|
|
|
Дата добавления: 2013-12-12; Просмотров: 3854; Нарушение авторских прав?; Мы поможем в написании вашей работы!