
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Расчет разветвленных цепей постоянного тока
|
|
|
|
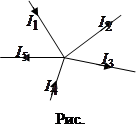 Закон Ома в интегральной форме позволяет рассчитывать практически любую электрическую цепь. Однако непосредственный расчет разветвленных цепей, содержащих замкнутые контуры, достаточно сложен. Эта задача упрощается при использовании правил Кирхгофа (немецкий физик, XIX в.).
Закон Ома в интегральной форме позволяет рассчитывать практически любую электрическую цепь. Однако непосредственный расчет разветвленных цепей, содержащих замкнутые контуры, достаточно сложен. Эта задача упрощается при использовании правил Кирхгофа (немецкий физик, XIX в.).
Любая точка разветвленной электрической цепи, в которой сходится не менее трех проводников тока, называется узлом. При этом ток, входящий в узел, считается положительным,
а ток, выходящий из узла – отрицательным (рис. 2.9).
Первое правило Кирхгофа сформулировано для узла электрической цепи: алгебраическая сумма сил токов в узле электрической цепи равна нулю, то есть

где n – число проводников, сходящихся в узле.
Таким образом, при указанных на рис. 2.9 направлениях токов в проводниках первое правило Кирхгофа запишется в виде

Первое правило Кирхгофа является следствием закона сохранения электрического заряда.
Второе правило Кирхгофа вытекает из закона Ома в интегральной форме для разветвленных цепей. Выделим в сложной электрической цепи замкнутый контур, состоящий из трех участков (рис. 2.10). Условимся обходить контур по часовой стрелке. Все токи, совпадающие по направлению
с выбранным направлением обхода контура, считаются положительными. ЭДС источников считаются положительными, если они создают ток,
направленный в сторону обхода контура. Применяя к отдельным участкам контура закон Ома,  запишем:
запишем:

Складывая почленно эти уравнения, получим

Таким образом, второе правило Кирхгофа гласит: в любом замкнутом контуре электрической цепи алгебраическая сумма ЭДС источников равна алгебраической сумме падений напряжений на отдельных участка этого контура, то есть

где n – количество источников тока в контуре; m – число участков в контуре.
При расчете сложных цепей постоянного тока с применением правил Кирхгофа следует придерживаться следующих рекомендаций:
1. Произвольно выбирают направления токов в ветвях цепи. Действительные направления токов в схеме определяются после завершения расчетов: если искомый ток получился положительным, то его направление было выбрано правильно, если отрицательным – его истинное направление противоположно выбранному.
2. Выбирают направления обхода замкнутых контуров цепи (по часовой или против часовой стрелке). Произведение 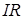 положительно, если ток на данном участке совпадает по направлению с направлением обхода; ЭДС, действующие по направлению обхода, считаются положительными, против направления обхода – отрицательными.
положительно, если ток на данном участке совпадает по направлению с направлением обхода; ЭДС, действующие по направлению обхода, считаются положительными, против направления обхода – отрицательными.
3. Составляют столько уравнений, чтобы их число было равно числу
неизвестных токов, то есть числу ветвей в схеме. По первому правилу Кирхгофа составляют n- 1 уравнений, где n – число узлов в схеме. Остальные уравнения составляют по второму правилу Кирхгофа.
4. Для проверки расчетов составляют баланс мощности в цепи: алгебраическая сумма мощностей источников тока равна сумме мощностей, рассеиваемых в ветвях схемы, то есть
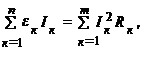
где n – число источников тока в цепи; m – количество ветвей в схеме.
Тема 14. Основные характеристики и закономерности магнитостатики
 Опыт показывает, что подобно тому, как в пространстве, окружающем электрические заряды, возникает электрическое поле (являющееся средой взаимодействия между ними), так в пространстве, окружающем токи и постоянные магниты, возникает силовое поле, называемое магнитным. Наличие такого поля обнаруживается по силовому воздействию на внесенные
Опыт показывает, что подобно тому, как в пространстве, окружающем электрические заряды, возникает электрическое поле (являющееся средой взаимодействия между ними), так в пространстве, окружающем токи и постоянные магниты, возникает силовое поле, называемое магнитным. Наличие такого поля обнаруживается по силовому воздействию на внесенные
в него проводники с током или постоянные магниты. Название «магнитное поле» связывают с ориентацией магнитной стрелки под действием силового поля, создаваемого током. Это явление впервые было обнаружено датским физиком Х. Эрстедом в 1820 г.
При пропускании по прямолинейному горизонтальному проводнику постоянного тока силой I находящаяся под ним магнитная стрелка поворачивается вокруг своей вертикальной оси, стремясь расположиться перпендикулярно проводнику с током (рис. 3.1). Ось стрелки тем точнее совпадает с этим направлением, чем больше сила тока и чем слабее влияние магнитного поля Земли. Эрстед обнаружил, что направление поворота северного полюса (N) стрелки под действием электрического тока изменяется на противоположное при изменении направления тока в проводнике.
В дальнейшем экспериментально исследовалось действие на магнитную стрелку электрического тока, протекающего по проводникам различной формы. Во всех случаях проводники с током оказывали ориентирующее действие на магнитную стрелку. Таким образом, при прохождении по проводнику электрического тока вокруг него возникает магнитное поле, действующее на помещенную в него магнитную стрелку.
Опыты показывают, что вокруг всякого движущегося заряда помимо электрического поля существует также и магнитное поле. Электрическое поле действует как на неподвижные, так и на движущиеся заряды. Важнейшая особенность магнитного поля состоит в том, что оно действует только на движущиеся в этом поле электрические заряды. Характер воздействия магнитного поля на ток зависит от формы проводника, по которому течет ток, от расположения проводника в силовом поле и от направления тока. Следовательно, чтобы охарактеризовать магнитное поле, надо рассмотреть его действие на определенный электрический ток.
Подобно тому, как при исследовании электростатического поля использовались точечные электрические заряды, для обнаружения и исследования магнитного поля используется замкнутый плоский контур с током – рамкас током, размеры которой малы по сравнению с расстоянием до токов, создающих магнитное поле. Ориентация контура в пространстве характеризуется направлением нормали 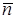 к плоскости рамки. В качестве положительного направления нормали принимается направление, связанное стоком правилом буравчика: за положительное направление нормали принимается направление поступательного движения винта, рукоятка (головка) которого вращается в направлении тока, текущего в рамке (рис. 3.2).
к плоскости рамки. В качестве положительного направления нормали принимается направление, связанное стоком правилом буравчика: за положительное направление нормали принимается направление поступательного движения винта, рукоятка (головка) которого вращается в направлении тока, текущего в рамке (рис. 3.2).
 Если поместить рамку с током в магнитное поле,
Если поместить рамку с током в магнитное поле,
то поле будет оказывать на рамку ориентирующее воздействие, поворачивая ее соответствующим образом. Это связано с определенным направлением магнитного поля. За направление магнитного поля принимается направление, вдоль которого располагается положительная нормаль к рамке. За направление магнитного поля может быть также принято направление, совпадающее с направлением силы, действующей на северный полюс магнитной стрелки, помещенной в данную точку. Так как оба полюса стрелки лежат в близких точках поля, то силы, действующие на оба полюса, равны друг другу. Следовательно, на магнитную стрелку действует пара сил, поворачивающая ее так, чтобы ось стрелки,
соединяющая S-N, совпадала с направлением поля.
Рамкой с током можно воспользоваться и для количественного описания магнитного поля. Так как рамка испытывает на себе ориентирующее действие поля, на нее в магнитном поле действует пара сил. Вращающий момент сил зависит от свойств магнитного поля в данной точке и от параметров самой рамки:
 (3.1)
(3.1)
где 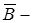 вектор индукции магнитного поля, являющийся силовой характеристикой поля;
вектор индукции магнитного поля, являющийся силовой характеристикой поля;  вектор магнитного момента рамки с током. Для
вектор магнитного момента рамки с током. Для
плоской рамки, по которой протекает ток силой I,
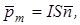
где S – площадь поверхности контура;  единичный вектор нормали
единичный вектор нормали
к поверхности рамки. Направление 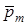 совпадает, таким образом, с направлением положительной нормали.
совпадает, таким образом, с направлением положительной нормали.
Если в данную точку магнитного поля помещать рамки с различными магнитными моментами, то на них будут действовать различные по величине вращающие моменты, однако отношение для всех контуров будет одним и тем же и поэтому может служить количественной характеристикой магнитного поля, называемой магнитной индукцией:
для всех контуров будет одним и тем же и поэтому может служить количественной характеристикой магнитного поля, называемой магнитной индукцией:

Таким образом, магнитная индукция в данной точке однородного поля определяется максимальным вращающим моментом, действующим на рамку с магнитным моментом, равным единице, когда нормаль к рамке перпендикулярна к направлению поля (аналог 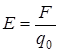 ).
).
Так как магнитное поле является силовым, его, по аналогии с электрическим полем, изображают с помощью линий магнитной индукции – линий, касательные к которым в каждой точке совпадают с направлением вектора 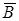 . Их направление определяется правилом буравчика: рукоятка винта, ввинчиваемого по направлению тока, вращается в направлении линий
. Их направление определяется правилом буравчика: рукоятка винта, ввинчиваемого по направлению тока, вращается в направлении линий
магнитной индукции.
Линии магнитной индукции всегда замкнуты и охватывают проводники с токами или постоянные магниты. Этим они отличаются от линий напряженности электростатического поля, которые являются разомкнутыми (начинаются на положительных зарядах, обрываются на отрицательных и вблизи поверхности заряженного тела направлены перпендикулярно к ней).
Согласно предположению французского физика А. Ампера, в любом
теле существуют микроскопические (молекулярные) токи, обусловленные движением электронов в атомах и молекулах. Эти токи создают свое
магнитное поле и могут поворачиваться в магнитных полях макроскопических токов (токов, текущих в проводниках). Так, если вблизи какого-то тела
(среды) поместить проводник с током, то есть макроток, то под действием его магнитного поля микротоки в атомах тела определенным образом ориентируются, создавая тем самым дополнительное магнитное поле. Поэтому вектор магнитной индукции 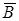 характеризует результирующее магнитное поле, создаваемое всеми макро- и микротоками, то есть при одном и том же токе I и прочих равных условиях вектор
характеризует результирующее магнитное поле, создаваемое всеми макро- и микротоками, то есть при одном и том же токе I и прочих равных условиях вектор 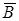 в различных средах будет иметь разные значения.
в различных средах будет иметь разные значения.
Магнитное поле, создаваемое макротоками, характеризуется вектором напряженности 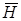 . Для однородной изотропной среды связь между векторами индукции
. Для однородной изотропной среды связь между векторами индукции 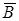 и напряженности
и напряженности 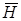 магнитного поля определяется выражением
магнитного поля определяется выражением
 (3.3)
(3.3)
где  магнитная постоянная,
магнитная постоянная,  магнитная проницаемость среды (безразмерная величина), показывающая, во сколько раз
магнитная проницаемость среды (безразмерная величина), показывающая, во сколько раз
магнитное поле макротоков усиливается за счет поля микротоков данной среды.
Единица напряженности магнитного поля – ампер на метр: 1 А/м –
напряженность такого поля, магнитная индукция которого в вакууме равна 4π·10-7 Тл.
|
|
|
|
Дата добавления: 2013-12-12; Просмотров: 698; Нарушение авторских прав?; Мы поможем в написании вашей работы!