Волновая оптика

Тема 21. Интерференция света

Поскольку свет – разновидность электромагнитных волн, должно
наблюдаться явление интерференции света – устойчивое чередование максимумов и минимумов освещенности при наложении двух или нескольких когерентных световых волн. Такие проявления интерференции света, как переливы тонкой пленки масла на поверхности воды, радужные цвета
мыльных пленок – люди наблюдали давно, но не могли дать им объяснения.

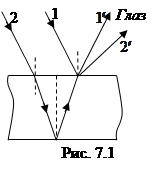Первым объяснил явление интерференции света английский ученый Т. Юнг (1773-1829), наблюдая отражение и преломление световых волн в тонких пленках (рис. 7.1). Белый свет, падая на тонкую пленку, частично (волна 1) отражается от верхней поверхности пленки, частично (волна 2), пройдя через пленку, отражается от ее нижней поверхности. Обе отраженные волны ( 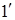и 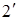) отличаются оптической длиной пути (больший путь проходит волна, отраженная от нижней поверхности пленки). При этом происходит наложение этих волн, результат которого зависит от угла падения света на пленку, ее толщины,
показателя преломления n вещества и длины волны 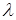. Усиление света происходит, когда преломленная волна 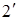отстает от отраженной волны 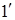на целое число длин волн

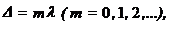
Где – оптическая разность хода волн.

Также Т. Юнг понял, что различие в цвете связано с различием в длине волны. Другими словами, вне нас в природе нет никаких красок (цветов) – есть лишь электромагнитные волны разной длины (белый свет немонохроматичен, он содержит электромагнитные волны разной длины – от 400 до 760нм). Человеческий глаз – это оптический прибор, способный
фиксировать различия в длинах световых волн, то есть обнаруживать разницу
в цвете. Из-за того, что зависит от длины волны, максимумы интерференционной картины для разных длин волн получаются в разных точках сетчатки глаза. Именно поэтому тонкие пленки имеют радужную окраску.

Необходимым условием интерференции волн является их когерентность – постоянство во времени разности фаз накладываемых волн. Этому условию удовлетворяют монохроматические волны, то есть волны строго определенной частоты (длины волны) и постоянной амплитуды. Однако ни один реальный источник не дает строго монохроматического света.
Поэтому волны, излучаемые любыми независимыми источниками света
(например, несколькими электрическими лампочками), всегда некогерентные. Чтобы понять это, необходимо обратить внимание на механизм излучения света атомами вещества.

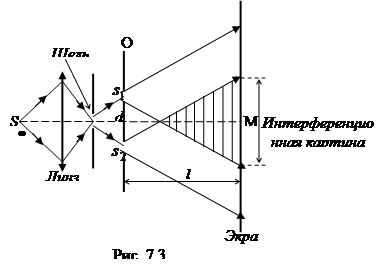Наиболее распространенным способом получения когерентных волн от обычных источников (не лазеров) является искусственное разделение световой волны, излучаемой одним источником, на две составные части, которые после прохождения различных оптических путей накладываются друг на друга и создают интерференционную картину. Реализовать этот способ можно с помощью различных приборов: зеркал Френеля, бипризмы Френеля, щелей Юнга и др. На рис. 7.3 приведена схема интерференционной установки Т. Юнга, которая была использована им для измерения длины световой волны (1803).

Результат интерференции в точке М (максимум или минимум освещенности) на экране зависит от длины световой волны и разности хода волн от когерентных источников 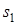и 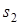. Если в плоскости О фаза колебаний
исходной световой волны была 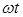, то в точке М первая волна возбудит
колебание 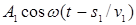, вторая волна – колебани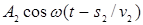е , где 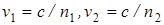– фазовые скорости соответственно первой и второй волны, 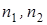– показатели преломления сред, в которых распространяются волны. Разность фаз колебаний, возбуждаемых волнами в точке М, равна

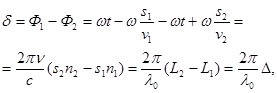
где λ ₀ – длина волны в вакууме; произведение геометрической длины пути s световой волны в данной среде на показатель преломления n этой среды
называется оптической длиной пути 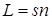; 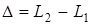– оптическая
разность хода.

Если оптическая разность хода равна целому числу длин волн в вакууме

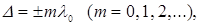(7.1)

является условием интерференционного максимума.

Если оптическая разность хода волн

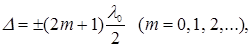(7.2)

является условием интерференционного минимума.

Из вышеизложенного следует, что явление интерференции обусловлено волновой природой света. Поэтому это явление используется для определения длин световых волн, для весьма точного (порядка 10^-7м) измерения размеров предметов, микронеровностей на поверхностях деталей, просветления оптики, определения показателя преломления прозрачных веществ. Рассмотрим некоторые применения интерференции.

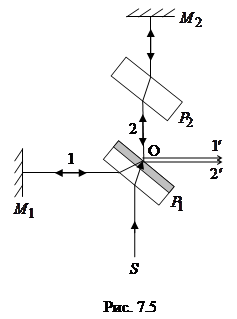
1. Для прецизионных измерений длин волн и размеров тел используются интерферометры. В качестве примера рассмотрим устройство и принцип работы интерферометра Майкельсона (рис. 7.5).

Монохроматический свет от источника S
падает под углом 45⁰ на плоскопараллельную пластинку Р₁, одна из сторон которой покрыта тонким слоем серебра и полупрозрачна. За счет этого в точке О исходный луч света
разделяется на две части: луч 1 (отражается от серебра) и луч 2 (проходит через слой серебра). Луч 1 отражается от зеркала М₁ и, возвращаясь обратно, вновь проходит через пластинку Р₁ (луч 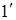). Луч 2 идет к зеркалу М₂, отражается от него, возвращается обратно и отражается от пластинки Р₁ (луч 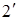). Таким образом, зеркала М₁ и М₂ играют роль
вторичных источников света, то есть обеспечивают условие когерентности лучей 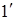и .

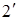Так как первый из лучей проходит пластинку Р₁ дважды, то для компенсации возникающей разности хода на пути второго луча устанавливается пластинка Р₂ (такая же, что и Р₁, но без слоя серебра). Поэтому пластинку Р₂ называют компенсатором.

Луч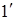и и 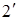когерентны, следовательно, будет наблюдаться интерференция, результат которой зависит от оптической разности хода луча 1 от точки О до зеркала М₁ и обратно, и луча 2 от точки О до зеркала М₂

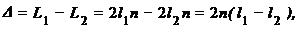
где 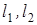– расстояния от точки О до зеркал М₁ и М₂, n – абсолютный показатель преломления воздуха.

Если 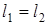, то   и наблюдается интерференционный максимум. Смещение одного из зеркал (с помощью микрометрических винтов) на расстояние 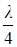приведет к появлению разности хода лучей

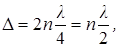
в результате чего возникнет интерференционный минимум:

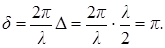
Таким образом, по незначительному смещению интерференционной картины можно судить о малом перемещении одного из зеркал и использовать интерферометр для точного измерения длины. Если поместить вместо одного из зеркал какую-либо деталь, можно по форме полос или колец контролировать качество ее обработки.

2. Особое место в применении интерференции занимает просветление оптики. При прохождении света через линзы или призмы от каждой из
поверхностей световой поток частично отражается. В сложных оптических системах, где много различных линз (биноклях, фотоаппаратах, перископах, дальномерах и др.), проходящий световой поток вследствие отражения может уменьшаться до 50% входящего в них света. Кроме того, отражения от поверхностей линз приводит к возникновению бликов. Для устранения этих
недостатков оптических приборов и применяется просветление оптики.

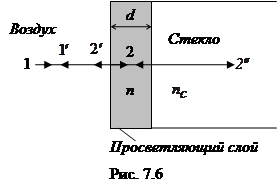
Сущность метода заключается в том, что поверхности линз покрываются тонкими пленками, создающими интерференционные явления (рис. 7.6). При этом накладываются когерентные световые лучи, отраженные от границ раздела воздух-пленка (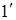) и пленка-стекло (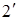). Толщину пленки d и показатели преломления стекла 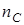и пленки n можно подобрать так, чтобы интерферирующие в отраженном потоке лучи гасили друг друга. Обычно толщина просветляющего слоя составляет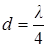
падающей световой волны. Тогда оптическая разность хода отраженных
лучей равна 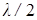, что соответствует условию минимума при интерференции. В результате достигается четкое изображение, и уничтожаются блики.
Добиться одновременного гашения в отраженном свете всех длин волн
невозможно, поэтому это делают для волн с 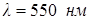(наиболее восприимчивой глазом длины волны). В связи с этим объективы с просветленной
оптикой имеют синевато-фиолетовый оттенок.

Просветляющие покрытия наносятся на поверхности линз или призм
путем их химической обработки (травление в кислоте), нанесением пленок фторидов при испарении в вакууме или механически.

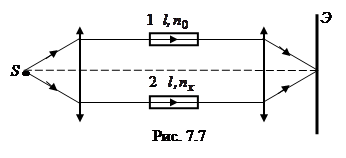
3. Для определения показателя преломления прозрачного вещества используются интерференционные рефрактометры (рис.7.7). На пути интерферирующих лучей помещаются две одинаковые кюветы 1 и 2 длиной l: одна заполнена газом с известным показателем преломления 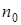, а другая – с неизвестным 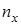. В результате возникает оптическая разность хода лучей

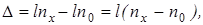
которая приводит к сдвигу интерференционных полос на экране. Зная, на какую часть ширины интерференционной полосы m сместилась интерференционная картина, находят неизвестный показатель преломления вещества:

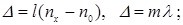
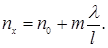
Тема 22. Дифракция света

Дифракцией света называется явление отклонения света от прямолинейного направления при его распространении в среде с резко выраженной оптической неоднородностью. Вследствие дифракции волны могут проникать через небольшие отверстия в экранах, огибать контуры непрозрачных предметов (попадать в область геометрической тени). Дифракцию можно наблюдать для волн любой природы, в том числе и механических (например, звук хорошо слышен за углом дома). Впервые явление дифракции научно описал и дал ему название Ф. Гримальди (1618-1663).

Для наблюдения явления дифракции света необходимо выполнение специальных условий, так как масштабы этого явления сильно зависят от соотношения размеров препятствия и длины волны. При длине волны, сравнимой с размерами препятствия, дифракция выражена очень сильно; в случае, если 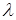значительно меньше размеров препятствия, дифракция выражена слабо, то есть свет распространяется прямолинейно.

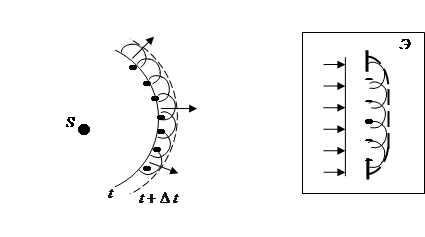
Первым явление дифракции попытался объяснить Х. Гюйгенс, выдвинув в 1690 г. принцип построения волнового фронта (принцип Гюйгенса): каждая точка, до которой доходит волновое возмущение, служит центром вторичных волн, а огибающая этих волн дает положение волнового фронта в следующий момент времени (рис. 7.8). В качестве примера рассмотрим плоскую волну, падающую нормально на отверстие в непрозрачном экране (рис. 7.9). Каждая точка приходящегося на отверстие волнового фронта является источником вторичной волны. Построив огибающую вторичных волн для некоторого момента времени, убедимся, что фронт волны заходит в область геометрической тени, то есть свет огибает края отверстия.

Рис. 7.8

Рис. 7.9

В 1816 г. О. Френель сделал принцип Гюйгенса физически более содержательным, дополнив его положением об интерференции вторичных волн. Согласно принципу Гюйгенса-Френеля, волновое возмущение в любой точке пространства является результатом интерференции вторичных волн, излучаемых каждым элементом некоторой волновой поверхности.

Для того чтобы определить результат дифракции (амплитуду световых колебаний) в некоторой точке пространства, Френель предложил разбивать волновую поверхность на отдельные участки (зоны Френеля) так, чтобы волны, посылаемые двумя соседними зонами в данную точку, приходили в противофазе. Таким образом, световые колебания, возбуждаемые
в данной точке пространства двумя соседними зонами, противоположны по фазе и при наложении должны взаимно ослаблять друг друга.

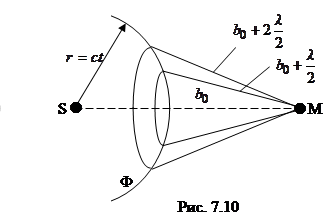Найдем в произвольной точке М амплитуду световой волны, распространяющейся в однородной среде от точечного источника S (рис. 7.10). Согласно принципу Гюйгенса-Френеля заменим действие источника S действием
фиктивных (вторичных) источников, расположенных на волновой поверхности Ф (поверхности сферы радиуса 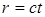с центром S). Амплитуда волны в точке М определяется результатом интерференции волн от вторичных источников, то есть необходимо сложить когерентные колебания, возбуждаемые всеми фиктивными источниками на волновой поверхности. Так как расстояния от них до точки М различны, то колебания будут приходить в различных фазах. Наименьшее расстояние от точки М до волновой поверхности равно b. Первая зона Френеля ограничивается точками волновой поверхности,
расстояния от которых до точки М равны 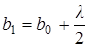. Границы второй зоны Френеля определяются соотношением 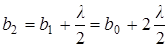и т. д. Так как колебания от соседних зон проходят до точки М расстояния, отличающиеся на 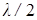, то в точку М они приходят в противофазе, и наблюдается интерференционный минимум. Поэтому амплитуда результирующего колебания в рассматриваемой точке

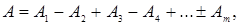(7.3)

где 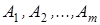– амплитуды колебаний, возбуждаемых соответственно первой, второй, …, m -зонами.

Общее число зон Френеля, умещающихся на полусфере очень велико, поэтому приближенно можно считать, что амплитуда 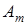колебаний от некоторой m-й зоны Френеля равна среднему арифметическому от амплитуд примыкающих к ней зон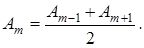

Тогда выражение (7.3) можно записать в виде

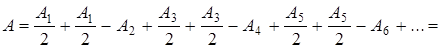
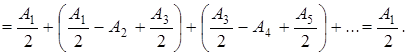(7.4)

Полученный результат показывает, что амплитуда результирующего светового колебания определяется действием только половины центральной зоны Френеля (все остальные вторичные волны гасятся в результате интерференции). Следовательно, распространение света от источника S к точке М происходит так, будто световой поток распространяется внутри очень узкого канала вдоль SM, то есть прямолинейно. Таким образом, принцип Гюйгенса-Френеля позволяет объяснить прямолинейное распространение света в однородной среде.

Поместим теперь на пути сферической волны, распространяющейся от точечного источника S, препятствие в виде непрозрачной пластины с круглым отверстием (дифракция на круглом отверстии). Для наблюдения дифракционной картины параллельно плоскости отверстия на расстоянии b расположен экран (рис. 7.11).

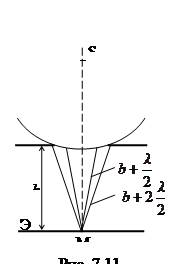Разобьем открытую часть волновой поверхности на зоны Френеля. Вид дифракционной картины зависит от числа зон Френеля, укладывающихся на ширине отверстия. Амплитуда результирующего светового колебания, возбуждаемого в точке М всеми зонами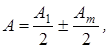

где знак «плюс» соответствует нечетному числу m зон Френеля, знак «минус» – четному числу зон Френеля.

Когда отверстие открывает нечетное число зон
Френеля, то амплитуда результирующего колебания (интенсивность света) в точке М будет больше, чем при свободном распространении волны, если четное – то амплитуда будет равна нулю. Если в отверстие укладывается одна зона Френеля, то в точке М
амплитуда 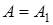, то есть вдвое больше, чем при отсутствии препятствия [см. формулу (7.4)]. Таким образом, дифракционная картина от круглого
отверстия вблизи точки М будет иметь вид чередующихся темных и светлых колец с центрами в точке М: если m четное, то в центре будет темное кольцо, если m нечетное – светлое кольцо, причем интенсивность убывает с увеличением расстояния от центра картины.

Дифракция на щели плоских световых волн. Пусть на узкую щель шириной 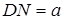, расположенную в непрозрачной преграде, нормально падает
плоская монохроматическая световая волна (рис. 7.12). За щелью помещена собирающая линза, в фокальной плоскости которой расположен экран для наблюдения дифракционной картины.

По принципу Гюйгенса-Френеля освещенная щель является источником вторичных световых когерентных волн, распространяющихся по всем направлениям и способных интерферировать друг с другом.

Рассмотрим направление, параллельное главной оптической оси линзы Л и совпадающее с направлением падающей волны (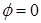). Линза соберет световые лучи этого направления в своем главном фокусе F. Все эти лучи до точки F проходят одинаковые оптические пути, поэтому в нее они придут в одинаковой фазе и, интерферируя, усилят друг друга. Следовательно,
в главном фокусе линзы всегда наблюдается максимум интенсивности I
света, который имеет вид ярко освещенной полосы, параллельной щели.

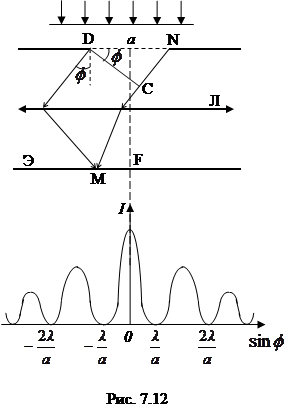Рассмотрим теперь лучи, идущие под углом 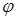к первоначальному
направлению распространения волны. Эти лучи линза соберет в точке М. Чтобы узнать, каков результат интерференции вторичных волн в данном случае, сделаем следующие построения. Проведем перпендикуляр DC
к направлению распространения вторичных волн. Тогда оптическая разность хода между лучами, идущими от крайних точечных источников D и N, равна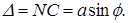

Далее воспользуемся методом зон Френеля. Для определения числа зон Френеля на участке 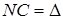разобьем его на отрезки, равные половине длины волны λ /2, и через точки разбиений проведем плоскости, параллельные DC. Эти плоскости разделят щель
на зоны Френеля, которые в данном случае представляют собой полоски, параллельные краям щели.

Число зон, укладывающихся в щели, зависит от длины волны и угла 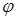(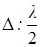). В свою очередь, от числа зон Френеля зависит результат наложения всех вторичных волн. Если число зон Френеля четное, то есть выполняется условие

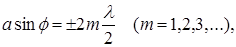(7.5)

то в точке М наблюдается дифракционный минимум (вторичные волны, идущие от двух соседних зон, погасят друг друга).

В направлениях, которым соответствует нечетное число зон Френеля, укладывающихся в щели, то есть при выполнении условия

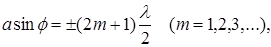(7.6)

наблюдается дифракционный максимум, обусловленный действием одной некомпенсированной зоны Френеля.

Из условий (7.5) и (7.6) можно найти направления лучей на точки экрана, в которых интенсивность света равна нулю

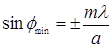(7.7)

или максимальна

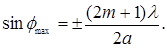(7.8)

Распределение интенсивности на экране, получаемое вследствие
дифракции, называют дифракционным спектром. При неизменной ширине щели максимумы интенсивности света различной длины волны приходятся на различные углы. Если щель освещать белым светом, то центральный (нулевой) максимум будет белым, а по обе стороны от него расположатся цветные максимумы первого порядка: согласно (7.8) красный свет (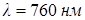) отклонится на больший угол, чем фиолетовый (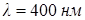). Между ними расположатся остальные цвета спектра.

Дифракционная решетка. Использование дифракции света на одной
щели затруднено из-за слабой видимости дифракционной картины. Поэтому
в практических целях применяется специальное устройство – дифракционная решетка.

Дифракционная решетка – спектральный прибор, предназначенный для разложения света в спектр и измерения длины световой волны. Простейшая одномерная решетка представляет собой совокупность большого числа регулярно расположенных препятствий и щелей на металлической или стеклянной пластинке (лучшие металлические решетки имеют до 2000 штрихов на один миллиметр поверхности, общая длина решетки составляет 100-150мм).

Если ширина каждой щели равна а, а ширина непрозрачных участков между щелями b, то величина 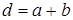называется периодом или постоянной дифракционной решетки.

Дифракционная картина на решетке определяется как результат интерференции волн, идущих от всех щелей (многолучевая интерференция света).

Пусть плоская монохроматическая волна падает нормально плоскости решетки (рис. 7.13). Так как щели находятся друг от друга на одинаковых расстояниях, то разность хода лучей,
идущих от двух соседних щелей, будет для данного направления 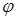одинакова в пределах всей дифракционной решетки:

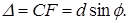
В направлениях (то есть для таких углов φ), в которых световые волны ни от одной из щелей не распространяются (свет от разных частей каждой щели полностью гасится в результате интерференции), они не будут распространяться и при N щелях. Следовательно, главные минимумы интенсивности будут наблюдаться в направлениях, для которых выполняется условие (7.5):

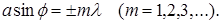
Вследствие взаимной интерференции волн действие одной щели будет усиливать действие другой, если

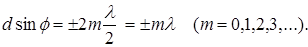(7.9)

Соотношение (7.9) выражает условие главных максимумов.

Кроме главных максимумов имеется большое число очень слабых
побочных максимумов, разделенных дополнительными минимумами. Условие дополнительных минимумов имеет вид

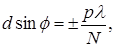(7.10)

где р= 1, 2, 3,…, кроме N, 2 N, 3 N и т.д.; N – число штрихов решетки.

Таким образом, после падения плоской волны на дифракционную
решетку происходит интерференция волн, дифрагировавших на щелях, что
и обусловливает сложную дифракционную картину на экране.

Для того чтобы прибор позволил достаточно точно зафиксировать обе спектральные линии, Разрешающей способностью (разрешающей силой) дифракционной
решетки называется безразмерная величина

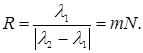(7.12)

Как следует из формулы (7.12), высокую разрешающую способность имеют решетки с большим числом штрихов N при наблюдении спектров высокого порядка m. Современные спектральные приборы содержат
дифракционные решетки с числом штрихов 500-2000 на 1мм.

Угловая дисперсия дифракционной решетки определяется величиной

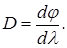(7.13)

Дифференцируя выражение (7.9), получим

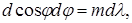
следовательно, угловую дисперсию дифракционной решетки можно определить по формуле

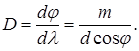
Тема 23. Поляризация света

Как отмечалось выше, свет представляет собой электромагнитные
колебания, распространяющиеся в виде электромагнитных волн с длиной волны порядка (3,8-7,6)∙10^-7 м. Электромагнитная волна характеризуется вектором напряженности 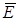электрического поля и вектором напряженности 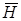магнитного поля. Эти векторы расположены во взаимно перпендикулярных плоскостях и колеблются в одинаковых фазах.

Колебания векторов 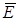и 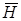в изотропной среде (среде, физические свойства которой одинаковы во всех направлениях) происходят перпендикулярно направлению распространения колебаний. Поэтому электромагнитные волны относятся к типу поперечных волн.

В большинстве случаев воздействие световых волн определяется вектором напряженности 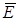электрического поля, так как явления, наблюдаемые в веществе под действием света (люминесценция, фотоэффект и др.), связаны с воздействием на электроны.

Электромагнитные волны, излучаемые светящимся телом, – это результат отдельных волн, которые испускаются его атомными осцилляторами. Вследствие того, что атомы беспрерывно изменяют свою пространственную ориентацию, изменяется с большой частотой и направление колебаний вектора 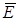результирующей световой волны.

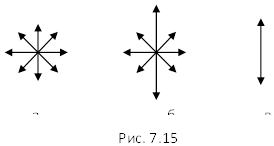
Если в световой волне колебания вектора напряженности 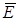электрического поля происходят по всевозможным направлениям в плоскости, перпендикулярной направлению распространения (к лучу), то свет называют естественным (рис. 7.15, а). Свет, в котором колебания светового вектора 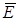каким-то образом упорядочены, называют поляризованным.

Частично поляризованным называется свет с преимущественным
направлением колебаний вектора 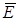(рис. 7.15, б). Если колебания вектора 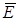(а, следовательно, и 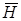) происходят только в одном направлении, перпендикулярном лучу, то свет называют плоскополяризованным (рис. 7.15, в).

Прибор, превращающий естественный свет в поляризованный, называют поляризатором. Он пропускает колебания, например, параллельные главной плоскости поляризатора и полностью задерживает колебания, перпендикулярные этой плоскости. В качестве
поляризаторов могут использоваться среды, анизотропные в отношении
колебаний вектора .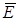

Прибор, определяющий направление колебаний (гасящий поляризованную волну) и предназначенный для анализа степени поляризации света, называют анализатором.

Один из способов получения поляризованного света состоит в использовании явления отражения и преломления света на поверхности диэлектрика. Пусть на черное зеркало (в этом зеркале устранено отражение от второй поверхности) падает естественный свет. Световые колебания, как и любые колебания, происходящие в одной плоскости, можно разложить по правилу параллелограмма на два колебания, происходящие в двух взаимно перпендикулярных плоскостях. Следовательно, естественный луч света можно представить как луч, в котором колебания происходят в двух взаимно перпендикулярных направлениях, например, в плоскости чертежа, которую считаем совпадающей с плоскостью падения (условно отмечаются стрелками) и в плоскости перпендикулярной (отмечаются точками). Эти два вида колебаний по-разному отражаются от зеркала из диэлектрика.

Если угол 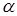падения света на границу раздела двух диэлектриков
(например, воздуха и стекла) с показателями преломления n₁ и n₂ не равен нулю, то отраженный и преломленный лучи оказываются частично поляризованными (рис. 7.17). В отраженном свете преобладают колебания, перпендикулярные плоскости падения, в преломленном луче – колебания, параллельные плоскости падения.

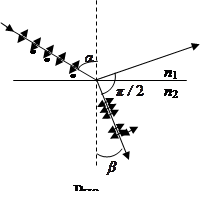Степень поляризации зависит от угла падения 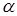. При угле падения, удовлетворяющем условию

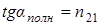(7.16)

(n ₂₁ – показатель преломления второй среды относительно первой), отраженный луч полностью поляризован, а преломленный луч поляризован максимально, но не полностью. Соотношение (7.16)
называется законом Брюстера. Угол 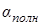называют углом Брюстера или углом полной поляризации.

Из закона Брюстера и закона преломления 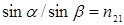следует, что при падении света на диэлектрик под углом 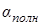луч, отраженный под этим углом, и луч преломленный взаимно перпендикулярны.

Двойное лучепреломление. В природе существуют кристаллы (например, исландский шпат), которые дают двойное лучепреломление. Это явление объясняется следующим образом.

Кристаллы – тела анизотропные, то есть их физические свойства,
например, скорость распространения световых колебаний, различны в разных направлениях. Но особенностью кристалла является то, что в нем можно выделить оптическую ось. Она характеризуется тем, что свойства кристалла одинаковы во всех направлениях, которые составляют с оптической осью кристалла любые равные углы. Необходимо отметить, что оптическая ось не есть определенная линия, а только определенное направление. Плоскость, проходящая через падающий луч и оптическую ось кристалла, называется главным сечением кристалла.

Скорость распространения света в кристалле зависит от угла 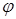между направлением колебаний и направлением главной оси кристалла: .

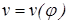Если луч света идет вдоль оптической оси кристалла, то все его колебания перпендикулярны оптической оси (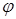 = 90⁰) и, следовательно, распространяются с одной и той же скоростью. Луч в этом случае не раздваивается, и двойного изображения нет.

Если луч света падает под некоторым углом 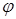к оптической оси
кристалла, то можно разложить колебания в падающем луче на два взаимно перпендикулярных колебания: колебания, происходящие в плоскости сечения, и колебания, происходящие в плоскости, перпендикулярной главному сечению.

Колебания, перпендикулярные главному сечению кристалла (обозначены точками), распространяются в кристалле с той же скоростью, что и колебания луча, идущего вдоль оптической оси, так как при любом угле падения они составляют с осью кристалла угол 90⁰.

Колебания, происходящие в плоскости главного сечения кристалла
(обозначены стрелками), распространяются с другой скоростью, так как они составляют с осью кристалла другой угол, равный 90⁰ - .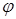

Так как скорость распространения колебаний в кристалле зависит от угла 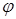, то есть 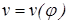, то колебания, перпендикулярные главному сечению, и колебания, лежащие в плоскости главного сечения, распространяются в кристалле с различной скоростью и, следовательно, имеют различный показатель преломления. Но при различном показателе преломления различны и углы преломления. В этом случае луч света раздваивается и дает двойное изображение. Лучи, колебания в которых перпендикулярны плоскости главного сечения, называют обыкновенными; лучи, колебания в которых происходят в плоскости главного сечения, называют необыкновенными.

Лучи обыкновенные и необыкновенные являются поляризованными
лучами: обыкновенный луч поляризован в плоскости главного сечения,
а необыкновенный луч – в плоскости, перпендикулярной плоскости главного сечения.

Призма Николя. Закон Малюса. Устройства, служащие для получения поляризованного света, называют поляризационными призмами. Поляризационная призма может служить и анализатором. Поляризационную призму Николя часто называют просто николь. Она представляет собой кристалл исландского шпата, имеющий форму параллелепипеда (рис. 7.18).

Кристалл разрезается наклонно по плоскости BEDP на две части, а затем склеивается канадским бальзамом. Показатель преломления канадского бальзама n= 1,549. Показатель преломления исландского шпата для обыкновенных лучей n _о = 1,658. Для необыкновенных лучей показатель преломления исландского шпата различен для разных направлений: для лучей, идущих параллельно длинным ребрам призмы, он равен n _e = 1,515.

Пусть естественный луч падает на нижнюю грань призмы (рис. 7.18, б)
в плоскости главного сечения (плоскости чертежа) под таким углом, что преломленные лучи, раздвоившись, идут почти параллельно продольным ребрам. Необыкновенный луч (е), дойдя до слоя канадского бальзама, вступает в него как в тело, более преломляющее и продолжает путь,
не отклоняясь, так как слой канадского бальзама очень тонок. Обыкновенный же луч (о) встречает слой бальзама как среду менее преломляющую, и так как угол падения его больше предельного угла, то этот луч испытывает полное отражение и поглощается зачерненной гранью призмы. Из призмы выходит один только необыкновенный луч, колебания в котором параллельны главному сечению.

Если на анализатор падает поляризованный луч, плоскость поляризации которого составляет угол 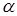с плоскостью поляризации анализатора, то интенсивность прошедшего через анализатор луча определяется законом Малюса:

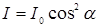, (7.17)

где 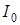– интенсивность луча, падающего на анализатор; I – интенсивность луча, выходящего из анализатора, без учета потерь в анализаторе в результате поглощения и рассеяния света.

Если пропустить естественный свет через два поляризатора, плоскости которых образуют угол 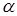, то из первого выйдет плоскополяризованный свет интенсивностью 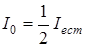, а из второго – свет интенсивностью 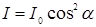. Таким образом, интенсивность света, прошедшего через два поляризатора,

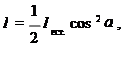
откуда 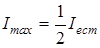(поляризаторы параллельны) и 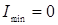(поляризаторы скрещены). В последнем случае будет полное затмение поля зрения.

Тема 24. Распространение света в веществе

Поглощение (абсорбция) света. Из опыта установлено, что по мере распространения плоской световой волны в веществе ее интенсивность уменьшается.

Поглощением светаназывается явление потери энергии волной, проходящей через вещество, вследствие преобразования энергии электромагнитной волны в другие формы – внутреннюю энергию вещества, энергию вторичного излучения других направлений и другого спектрального состава. В результате абсорбции интенсивность света при прохождении через вещество уменьшается.

Поглощение света может вызывать нагревание вещества, возбуждение, ионизацию атомов или молекул, фотохимические реакции и другие процессы в веществе.

В XVIII в. был экспериментально установлен закон поглощения света веществом, называемый законом Бугера. Согласно этому закону интенсивность плоской волны монохроматического света уменьшается по мере прохождения через поглощающую среду по экспоненциальному закону:

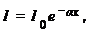(7.18)

где I ₀, I – интенсивности плоской монохроматической световой волны на входе и выходе слоя поглощающей среды толщиной х; 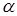– коэффициент поглощения, зависящий от химической природы вещества, его состояния, длины волны λ и не зависящий от интенсивности света (~).

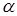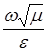У одноатомных газов и паров металлов атомы расположены на значительных расстояниях друг от друга, и такие вещества обладают близким к нулю коэффициентом поглощения 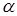. Лишь для очень узких спектральных областей (примерно 10^–12 – 10^–18 м) наблюдаются резкие максимумы, так называемый линейчатый спектр поглощения. Эти линии соответствуют частотам собственных колебаний электронов в атомах: дискретные частоты интенсивного поглощения света совпадают с частотами собственного излучения возбужденных атомов газов.

У диэлектриков коэффициент поглощения невелик (примерно 10^–3 –
10^–5см ^{– 1}), однако у них наблюдается выборочное поглощение света в определенных интервалах длин волн, когда 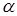резко возрастает, и появляются сравнительно широкие полосы поглощения. Другими словами, диэлектрики имеют сплошной спектр поглощения. Это объясняется тем, что в диэлектриках нет свободных электронов, и поглощение света обусловлено явлением резонанса при вынужденных колебаниях электронов в атомах вещества.

У металлов коэффициент поглощения имеет большое значение (10³ –
10⁵см ^{– 1}) и поэтому металлы являются непрозрачными для света. Это объясняется тем, что в металлах из-за наличия свободных электронов, движущихся под действием электрического поля световой волны, возникают быстропеременные токи, сопровождающиеся выделением джоулевой теплоты. Поэтому энергия световой волны быстро уменьшается, превращаясь
во внутреннюю энергию металла. Чем выше проводимость металла, тем сильнее в нем поглощение света.

Рассеяние света. Рассеяниемназывается явление преобразования света веществом, сопровождающееся изменением направления движения световой волны и проявляющееся как несобственное свечение вещества.

Несобственное свечение вещества обусловлено вынужденными колебаниями электронов в атомах или молекулах рассеивающей среды под действием падающего света. Как показал Л.И. Мандельштам, рассеяние света возможно только в оптически неоднородной среде, показатель преломления которой нерегулярно изменяется от точки к точке. Примерами таких сред являются мутные среды – аэрозоли (дым, туман), эмульсии, матовые стекла – то есть среды, содержащие мелкие частицы, показатель преломления которых отличается от показателя преломления окружающей среды.

В случае оптически однородной среды ее малые одинаковые объемы, содержащие равное и большое число молекул, можно рассматривать как когерентные источники вторичных волн. В такой среде рассеяние света отсутствует, так как для всех направлений, отличных от направления первичного пучка света, вторичные волны взаимно гасятся из-за интерференции.

В случае оптически неоднородной среды расстояние между малыми по размеру инородными частицами мутной среды значительно больше длины волны света λ, то есть эти неоднородные частицы будут вести себя как независимые вторичные источники света. Излучаемые ими волны будут некогерентными между собой и при наложении не могут интерферировать, поэтому оптически неоднородная среда рассеивает свет по всем направлениям.

Дисперсия света. В отношении электромагнитных волн термин «дисперсия» понимается в смысле спектрального разложения сложного излучения (на его составные части) по частотам или длинам волн. Причиной такого разложения является зависимость фазовой скорости от частоты или длины волны:

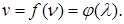
Поскольку 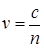, где с – скорость света в вакууме, n – показатель преломления среды, то можно сделать вывод о том, что существование дисперсии света в среде обусловлено зависимостью показателя преломления среды
от частоты или длины волны:

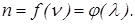
Следствием дисперсии является разложение в спектр пучка белого света при прохождении его через призму, изготовленную из какой-либо прозрачной среды: на экране, установленном за призмой, наблюдается радужная полоса, которая называется призматическим или дисперсионным спектром. Впервые это явление наблюдал еще И. Ньютон.

Зависимость показателя преломления среды n от длины волны λ нелинейная (рис. 7.19). Величина

,

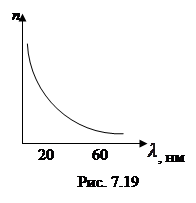называется дисперсией вещества и показывает, как быстро изменяется показатель преломления среды с длиной волны. Если показатель преломления для прозрачных веществ с уменьшением λ монотонно увеличивается, то дисперсия называется нормальной. Если с уменьшением λ показатель преломления среды также уменьшается, то дисперсию называют аномальной. Аномальная дисперсия наблюдается в областях частот, соответствующих полосам интенсивного поглощения света в данной среде. В табл. 7.1 приведено значение показателя преломления некоторых веществ в зависимости от длины волны.

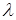,		n
мкм	Флюорит	Кварц	Каменная соль
0,2 1,6 3,2	1,50 1,43 1,41	1,65 1,53 1,47	1,75 1,53 1,51

Дата добавления: 2013-12-12